1. Интерференция

– оптическая разность хода;

– зависимость разности фаз от оптической разности хода;

,– условие максимума при интерференции;

,– условие минимума при интерференции;

,– координатаm^ойсветлой интерференционной полосы;

,–координатаm^ойтемной интерференционной полосы;

– ширина интерференционной полосы;

– оптическая разность хода при отражении от тонкой пленки;

– радиус темных колец Ньютона в отраженном свете.

2. Дифракция

– радиусm^ойзоны Френеля при дифракции на круглом отверстии;

;m=±1, ±2, ±3… – условие минимума при дифракции на щели;

;m=0; ±1.43, ±2.46, ±3.47, ±3.48… – условие максимума при дифракции на щели;

;m=1, 2, 3… – приблизительное условие максимума при дифракции на щели;

; m=0, ±1, ±2, ±3… – условие главных максимумов при дифракции на дифракционной решетке;

; m=±1, ±2, ±3… – условие главных минимумов при дифракции на дифракционной решетке;

;m≠0, ±N, ±2N, ±3N,… – условие дополнительных минимумов при дифракции на дифракционной решетке;

– угловая дисперсия дифракционной решетки;

– линейная дисперсия дифракционной решетки;

– разрешающая способность оптического прибора, гдеδΨ – минимальное угловое расстояние между точечными источниками, изображения которых разрешаются;

– угловой радиус первого темного кольца при дифракции на круглом отверстии;

– разрешающая способность спектрального прибора;

– разрешающая способность дифракционной решетки;

; m=±1, ±2, ±3… – формула Брэггов-Вульфа.

4. Поляризация, поглощение

– закон Брюстера;

– закон Малюса;

;– угол поворота плоскости поляризации оптически активными веществами;

– закон Бугера-Ламберта.

Примеры решения задач

Задача 3

Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластине. Радиус десятого темного кольца Ньютона в отраженном свете (длина волны 589 нм) равен 1.25 мм. Свет падает нормально. Определить фокусное расстояние линзы, если она изготовлена из стекла с показателем преломления 1.6.

Решение:

Фокусное расстояние линзы определяется радиусами кривизны её поверхностей и показателем преломления: . ЗдесьR₁=R,R₂→ ∞ (плоская поверхность); тогда, или.

Радиус m-го темного кольца Ньютона в отраженном свете, откуда, а.

Ответ: F=0.44 м.

Задача 4

Ширина прозрачного аи непрозрачногоbучастков дифракционной решетки связаны с длиной волны так:а=0.5b=4. Определить углы, соответствующие первым трем наблюдаемым максимумам.

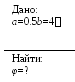
Решение:

Условие главных максимумов при дифракции на решётке: , гдеm=0, ±1, ±2, ±3…. Найдём постоянную дифракционной решётки:d=a+b=a+2a=3a=12, посколькуb=2a,а=4. Получим:, или,.

По условию постоянная решётки dкратна ширине щелиa: d=3a, поэтому один и тот же уголφбудет соответствовать и главному максимуму с номеромm, и главному минимуму с номеромm’, еслиm= 3m’. В этом случае условие главных максимумов можно записать так:, что является также условием главных минимумов:, и главный максимум не будет наблюдаться. Таким образом, не будут наблюдаться максимумы с номерамиm=3, 6, 9, … . Искомыми первыми тремя наблюдаемыми будут максимумы с номерамиm=1, 2 и 4. Подставляем в расчётную формулу эти значения:

,,.

Задача 5

Плоско поляризованный свет падает на николь так, что угол между плоскостями поляризации света и главного сечения николя равен 60⁰. Определить толщину николя, если интенсивность света уменьшилась в 6 раз. Коэффициент отражения на грани призм=0.1, коэффициент поглощения.

Решение:

Пусть I₀– интенсивность света на входе в призму Николя, I – на выходе. Для идеального николя по закону Малюса– доля прошедшей световой энергии. Однако здесь надо учесть ещё две причины уменьшения интенсивности света: отражение на грани призмы и поглощение. По условию задачи 10% света отражается, 90% – проходит. Доля прошедшей световой энергии составит η ₁=(1– ρ). Толщину слоя поглощающего вещества можно найти из закона Бугера:, то есть доля прошедшей световой энергии от всей падающей составляет, если учитывать только поглощение. Теперь учтём все три процесса:, или. Отсюда, и далее после логарифмирования;. После подстановки:.

Ответ: l = 0.015 м =1.5 см.