34

Индивидуальные задания

«Строительство» бакалавры (2-ой семестр)

1. Колебания и волны

1.Механические колебания и волны.

;;– смещение из положения равновесия, скорость и ускорение колеблющейся точки;

– дифференциальное уравнение гармонических колебаний;

– возвращающая сила при гармонических колебаниях;

;;– период колебаний пружинного, математического и физического маятников;; – закон сохранения энергии;

;– амплитуда и начальная фаза результирующего колебания при сложении однонаправленных колебаний одинаковой частоты;

– уравнение траектории точки, колеблющейся с одинаковыми частотами в перпендикулярных направлениях;

– дифференциальное уравнение затухающих колебаний;

– круговая частота собственных незатухающих колебаний;

– коэффициент затухания;

– сила сопротивления при затухающих колебаниях;

– уравнение затухающих колебаний;

– круговая частота затухающих колебаний;

– амплитуда затухающих колебаний;

– логарифмический декремент затухания;

(здесь) – дифференциальное уравнение вынужденных колебаний;

;;– смещение из положения равновесия, амплитуда и фаза вынужденных колебаний;– резонансная частота;

,– уравнения плоской и сферической волн;

– волновое число (волновой вектор);

– длина волны;

;– скорость распространения продольных и поперечных волн в твердом теле;

– скорость звука в газе (для воздуха);

– скорость распространения поперечной волны по струне.

2.Электромагнитные колебания и волны.

Колебательный контур

а) Свободные незатухающие колебания

– закон сохранения энергии;

– дифференциальное уравнение свободных колебаний;

– зависимость заряда на конденсаторе от времени при свободных незатухающих колебаниях в колебательном контуре;

– период колебаний в колебательном контуре;

– круговая частота свободных колебаний в колебательном контуре;

– длина волны, на которую настроен колебательный контур (c– скорость света в вакууме);

б) Свободные затухающие колебания

– дифференциальное уравнение затухающих колебаний;

– зависимость заряда на конденсаторе от времени при затухающих колебаниях в колебательном контуре;

– коэффициент затухания;

– циклическая частота затухающих колебаний;

– определение логарифмического декремента затухания;

– связь логарифмического декремента и коэффициента затухания;

– добротность колебательного контура;

в) Вынужденные колебания

– дифференциальное уравнение вынужденных колебаний для последовательной цепи переменного тока;

– зависимость силы тока от времени для последовательной цепи переменного тока;

– закон Ома для переменного тока;

– емкостное сопротивление;

– индуктивное сопротивление;

– полное сопротивление цепи переменного тока;

– тангенс сдвига фаз между током и напряжением в цепи переменного тока.

Примеры решения задач.

Задача 1.

Найти частоту колебаний груза массой m=0.2 кг, подвешенного на пружине и помещенного в масло, если коэффициент сопротивления в маслеr=0.5 кг/с, а коэффициент жесткости пружиныk=50 Н/м .

Р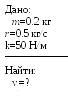ешение

Колебания груза в масле являются затухающими, их круговая частота:

,

где – круговая частота собственных незатухающих колебаний;– коэффициент затухания. Тогда частота затухающих колебаний.

Ответ: ν_.=2.51 Гц.

Задача 2

Колебательный контур состоит из конденсатора емкостью 2.66 нФ и катушки без сердечника, намотанной из медного провода диаметром 0.5 мм (витки вплотную, толщиной изоляции пренебречь). Длина катушки 20 см. Найти логарифмический декремент затухающих колебаний. Удельное сопротивление меди равно 1.7^.10^-8Ом · м.

Решение

Логарифмический декремент затухания выразим через период затухающих колебаний

(1)

и коэффициент затухания

:, (2)

(3)

а циклическую частоту ω_Ззатухающих колебаний – через собственную частоту контура

: (4)

. (5)

Здесь R– активное сопротивление катушки, а– её индуктивность:

. (6)

Число витков катушки равно , так как витки расположены вплотную и толщина изоляции провода мала. Площадь сечения катушки выразим через её радиусr:. Тогда из (6) получим:, или

. (7)

Активное сопротивление Rкатушки определяется длиной провода(– длина одного витка) и его сечением:, или. Таким образом, из (2) и (7) получим:; или

. (8)

Теперь выразим частоту собственных колебаний из (4) и (7): ;; а затем – частоту затухающих колебаний из (5) и (8):;

. (9)

Уравнения (1), (3) и (9) дают: ,. Окончательно:, или. Подставим численные значения:.

Ответ: .