Взаимное положение прямой и плоскости, двух плоскостей

Прямая может располагаться относительно плоскости параллельно, пересекать ее и в частном случае пересекать под прямым углом.

Прямая параллельна плоскости, если она параллельна прямой, принадлежащей данной плоскости.

Рассмотрим пример (рис. 43, а). Пусть дана плоскость Р, заданная треугольникомАВС и фронтальная проекция прямой l, проходящая через произвольную точку К. Требуется через точку К провести горизонтальную проекцию прямой l параллельную плоскости Р.

Для того, чтобы через точку К провести прямую параллельную плоскости Р(АВС), необходимо построить прямую проходящую через точку К и параллельную любой прямой, принадлежащей плоскости Р (рис. 43, б). Проведём прямую m, принадлежащую плоскости Р(АВС) и параллельную прямой l. На эпюре уже задана фронтальная проекция l₂ прямой l, поэтому проведем m₂ || l₂, найдем проекции точек 1₂ и 2₂ на сторонах треугольника В₂С₂ и А₂С₂, затем спроецируем их на горизонтальную плоскость и проведем горизонтальную проекцию m₁ прямой m. Через К₁ проведем l₁ || m₁. Прямая l || Р(АВС), т. к. она параллельна прямой m, принадлежащей плоскости Р.

Рис. 43

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости (рис. 44, а).

а) б)

Рис. 44

На эпюре (рис. 44, б) для удобства построения в качестве пересекающихся прямых следует брать горизонталь и фронталь (или горизонтальный и фронтальный следы плоскости), т.к. прямой угол между отрезком прямой и горизонталью проецируется в натуральную величину на П₁ (то же между горизонтальным следом и отрезком прямой), а прямой угол между отрезком прямой и фронталью проецируется в натуральную величину на П₂ (то же между фронтальным следом и отрезком прямой).

Рассмотрим пример (рис. 45). Требуется провести через точку А перпендикуляр к плоскости Р, заданной треугольником АВС.

Известно, что фронтальная проекция перпендикуляра к плоскости перпендикулярна к фронтальной проекции фронтали плоскости, а горизонтальная – к горизонтальной проекции горизонтали плоскости. На чертеже черезА₂ проводим фронтальную проекцию l₂ перпендикуляра l перпендикулярно к фронтальной проекции f₂ фронтали, а горизонтальную его проекцию l₁ – перпендикулярно к проекции h₁ горизонтали через А₁. Фронталь и горизонталь в плоскости строится, как это рассмотрено на рис.45.

Плоскости могут располагаться параллельно, пересекаться и в частном случае пересекаться под прямым углом.

Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

Рассмотрим пример. Пусть дана плоскостьР, заданная треугольником АВС и произвольная точка К. Требуется через точку К провести плоскость Г параллельную Р (АВС). Для того чтобы через точку К провести плоскость параллельную плоскости Р (АВС), достаточно построить две пересекающиеся прямые, параллельные двум пересекающимся прямым плоскости Р, так чтобы точка К принадлежала этим прямым. Например, проведём прямую m || AB, на эпюре m₁ || А₁B₁ и m₂ || А₂B₂ и прямую l || BC, на эпюре l₁ || B₁C₁ и l₂ || B₂C₂. Две пересекающиеся прямые m и l определяют плоскость Г. Плоскость Г || Р, так как две пересекающиеся прямые m и l, принадлежащие плоскости Г, параллельны двум пересекающимся прямым АВ и ВС, принадлежащим плоскости Р.

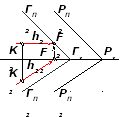
На рис. 46 показано построение параллельных плоскостей, заданных следами. Как известно, горизонтали параллельных плоскостей параллельны между собой, параллельны между собой и фронтали. Также одноименные следы параллельных плоскостей соответственно параллельны между собой. Необходимо через точку К провести плоскость Г || Р (рис. 46, а). Через точку К проводят горизонталь искомой плоскости – h₁ || P_П1, h₂ || х. Затем находят фронтальный след горизонтали F₂ и через него параллельно фронтальному следу плоскости P_П2 проводят фронтальный след искомой плоскости Г_П2, находят точку схода следов Г_Х на оси х и проводят след Г_П1 параллельно P_П1 (рис. 46, б).

а) б)

Рис. 46

Две плоскости взаимно перпендикулярны, если одна из плоскостей содержит прямую перпендикулярную второй плоскости.

Если прямаяl перпендикулярна плоскости P, то любая плоскость, проведенная через эту прямую, будет также перпендикулярна плоскости P. Поэтому через прямую l можно провести бесконечное множество плоскостей, что приводит к вариативности решения задач (рис. 47).

Рассмотрим два случая построения прямой перпендикулярной плоскости (на рис. 48, а – б плоскость задана следами, на рис. 48, в – треугольником). Исходя из выше рассмотренных построений (рис. 44), сначала необходимо в плоскости построить горизонталь и фронталь. Затем провести прямую l, перпендикулярную заданным плоскостям. На рис. 1, бlP,l₁P_П1,l₁ h₁иl₂P_П2,l₂ f₂. На рис. 48, в прямаяlпроведена перпендикулярно плоскости треугольникаАВСчерез точкуА(lАВС,l₁ h₁иl₂ f₂). Условие перпендикулярности выполнено, и теперь необходимо задать плоскость любым из известных способов. На рис. 48 плоскость задана пересекающимися прямымиl∩m=К. ТочкаКна прямойlвзята произвольно. Одна из прямых плоскости – перпендикулярl, поэтому вторую прямуюmможно провести под любым углом.

Так как через току Кможно провести множество прямых, то решение задачи может иметь множество вариантов (рис. 48, а).

а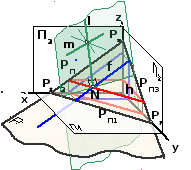) б) в)

Рис. 48

Двумя основными позиционными задачами, рассматриваемыми в этом разделе, являются:

задача на пересечение прямой общего положения с плоскостью общего положения;

задача на пересечение двух плоскостей общего положения.

 Прежде чем решать эти основные позиционные задачи рассмотрим частные случаи решения задач, когда геометрические образы занимают частное положение.

 Рассмотрим построение проекций точки К – точки пересечения прямой l общего положения с фронтально проецирующей плоскостью Р. На рис.49 плоскость задана следами (а), параллельными прямыми (б), треугольником (в).

Фронтальная проекция фронтально проецирующей плоскости вырождается в прямую, а на рис. 49, а совпадет с фронтальным следом плоскости. Поэтому проекция К₂ точки пересечения должна лежать на этой прямой или на фронтальном следе плоскости. Точка принадлежит прямой l и плоскости Р. Поэтому проецируем точку К на горизонтальную проекцию l₁ прямой l.

Дополним эпюры изображением видимых и невидимых участков прямой l , плоскость Р считаем непрозрачной. Часть прямой справа до точки К располагается выше плоскости Р, поэтому на П₁ проекция этой части прямой видима до точки К₁, другая часть прямой – невидима. Проекция прямой l на плоскости П₂ будет полностью видимой, так как плоскость вырождается в прямую и не перекрывает проекцию l₂.

a

а₂  b₂

) б) в)

Рис. 49

Далее найдем точку пересечения прямой l с горизонтальной плоскостью P, заданной ее фронтальным следом Р_П2.

В данном случае (рис. 50) плоскость Р параллельна П₁ и, следовательно перпендикулярна к фронтальной плоскости проекций. Для плоскости Р в системе дан только фронтальный след Р_П2 параллельный оси проекций х. Очевидно, что фронтальная проекция искомой точки пересечения должна лежать как на следе Р_П2, так и на фронтальной проекции прямой l (К₂  l₂, К₂  Р_П2  К₂ = l₂ ∩ Р_П2). По проекции К₂ находим К₁ на l₁.

Так как правая часть прямой до точки К находится под плоскостью Р, то на чертеже соответствующая часть горизонтальной проекции изображена штриховой линией.

На рис.51 представлены случаи построения точки пересечения фронтально проецирующей прямой с плоскостью общего положения, заданной следами (рис. 51, а), треугольником (рис. 51, б), прямой и точкой вне прямой (рис. 51, в). Так как прямая l на П₂ проецируется в точку, то проекция прямой совпадет с проекцией точки пересечения (К₂  l₂). На первых двух эпюрах горизонтальная проекция К₁ найдена через горизонталь h, а на третьем через прямую общего положения n.

а) б) в)

Рис. 51

Мы рассмотрели некоторые частные случаи пересечения прямой с плоскостью. Во всех этих случаях на эпюре одна из проекций точки пресечения была определена.

Теперь рассмотрим частные случаи построения линии пересечения двух плоскостей. Построение линии пересечения двух плоскостей сводится к нахождению двух точек, общих для обеих заданных плоскостей, или одной такой точки при известном направлении искомой линии.

На рис.52 и 53 для построения линии пересечения плоскостей можно использовать точку N пересечения следов P_П1 и Г_П1 и точку N' пересечения следов P_П2 и Г_П2. Прямая NN', проходящая через эти точки, является искомой линией пересечения.

На рис.53 проекция линии пересечения NN' совпадает со следом P_П1, так как плоскость Р является горизонтально проецирующей.

В случае на рис. 54 фронтальные следы плоскостей параллельны. Это значит, что искомая прямая параллельна плоскости П₂ и для плоскостей P и Г является фронталью. Чтобы провести эту фронталь, достаточно построить одну принадлежащую ей точку. Используем точку К пересечения следов P_П1 и Г_П1. Построив проекции К₁ и К₂, проводим l₁ параллельно оси х, а l₂ – параллельно следам P_П2 и Г_П2.

Г_х

Рис. 52 Рис. 53 Рис. 54

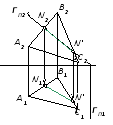
На рис. 55 представлены случаи построения линии пересечения горизонтальной плоскости с плоскостью общего положения, заданной треугольником (рис. 55, а) и следами (рис. 55, б). Так как Р || П₁, то линия пересечения является горизонталью. Чтобы построить эту горизонталь, достаточно построить две точки N и N', общие для обеих заданных плоскостей (рис. 55, а), или одну точку при известном направлении искомой линии (рис. 55, б).

На эпюре (рис. 56) одна из плоскостей фронтально проецирующая, а другая общего положения, заданная треугольником. Фронтальная проекция N₂N'₂ линии пересечения NN' совпадет со следом Г_П2, так как Г  П₂.

а) б)

Рис. 55 Рис. 56

Далее рассмотрим общие случаи решения основных позиционных задач, когда геометрические образы занимают общее положение.

 В общем случае для построения точки К пересечения прямой l с плоскостью P необходимо выполнить следующие построения (рис. 57):

1. Через данную прямую l провести вспомогательную плоскость частного положения Г (l  Г);

2. Построить линию NN' пересечения данной плоскости P и вспомогательной Г (Р ∩ Г = NN');

3. Определить положение точки К пересечения прямых – данной l и построенной NN' (l ∩ NN' = К);

4. Определить видимость прямой l, используя конкурирующие точки.

Далее представлены случаи решения задачи на пересечение прямой общего положения с плоскостью общего положения: плоскость задана треугольником (рис. 58); плоскость задана следами (рис. 59).

Применяя выше приведенный алгоритм построения точки пересечения прямой с плоскостью, проводим через прямую l фронтально-проецирующую плоскость Г и строим линию NN' пересечения обеих плоскостей – заданной и проведенной через l (рис. 58, а). Искомая точка К пересечения прямой l с плоскостью треугольника АВС находится в точке пересечения NN' с l.

Для определения участков прямой l, которые будут закрыты треугольником, следует воспользоваться анализом положения точек на скрещивающихся прямых (рис. 58, б). Например, точки 1 и N' находятся на скрещивающихся прямых l и ВС. Фронтальные проекции этих точек совпадают (точки 1 и N' – фронтально конкурирующие точки), т.е. точки 1 и N' одинаково удалены от П₁. Но расстояния их от П₂ различны, т.е. точка 1 находится дальше от П₂, чем точка N'. Поэтому по отношению к П₂ точка 1 закрывает точку N'. Следовательно, прямая l проходит перед треугольником АВС до точки К. Начиная от точки К влево прямая l закрывается треугольником, и поэтому этот участок показан штриховой линией.

Для выявления невидимого участка на горизонтальной проекции прямой l рассмотрим точки 2 и 3, лежащие соответственно на прямых l и АВ. Эти точки являются горизонтально конкурирующими – их проекции совпадают на П₁. Если смотреть на эти точки сверху, то сначала видна точка 2. Следовательно, прямая l в этом месте закрыта треугольником АВС, и участок ее проекции от точки К до точки 3 должен быть показан штриховой линией. В данном случае точка К оказалась внутри контура треугольника АВС. При другом взаимном положении пересекающихся геометрических образов возможен случай, когда точка К окажется вне треугольника. Это означает, что прямая l пересекает плоскость, заданную треугольником АВС, вне контура этого треугольника.

На рис. 59 для нахождения точки пересечения прямой с плоскостью через прямую l проводят горизонтально проецирующую плоскость Г (след Г_П1 совпадает с l₁) и строят линию пересечения плоскостей Г и P, используя точкиN и N' пересечения их одноимённых следов. Искомая точка К находится в точке пересечения NN' с l (l₂ ∩ N₂N₂' = К₂). Видимость прямой определяют на основании анализа положения точек (используя конкурирующие точки). Например, взяв горизонтально конкурирующие точки 1 (1  l) и N (N  P_П1), видно, что точка 1 располагается выше относительно П₁, чем точка N. Следовательно прямая l слева до точки К видима. За точкой К прямая показана штриховой линией – она невидима. Аналогично определяется видимость на фронтальной проекции.

Далее рассмотрим построение линии пересечения двух плоскостей общего положения. Как известно, построение линии пересечения двух плоскостей сводится к нахождению двух точек – общих для обеих заданных плоскостей. В данном случае обе точки можно найти, выполнив следующие построения (рис. 60):

1. Ввести две вспомогательные плоскости (посредники) частного положения Р и Р';

2. Построить линии a, а' и b, b' пересечения данных плоскостей (Г и ) и вспомогательных Р и Р':

Р ∩ Г = а, Р ∩  = b;

Р' ∩ Г = а', Р' ∩  = b';

3. Определить положение точек N и N' пересечения прямых a и b и прямых a' и b' соответственно:

a ∩ b = N; a' ∩ b' = N';

4. Соединить точки N и N', которые являются общими для обеих заданных плоскостей Г и . NN' – искомая линия пересечения плоскостей;

5. Определить видимость плоскостей Г и .

На рис. 61 найдена линия пересечения плоскостей, одна из которых задана параллельными прямыми а и b, а другая пересекающимися c и d.

Для определения общих точек данных плоскостей введены две вспомогательные горизонтальные плоскости уровня Р и Р' и построены линии пересечения этих плоскостей с заданными Г (a || b) и  (с ∩ d ). Через точки N и N' пересечения этих линий проходит искомая прямая. Прямые 1-2 и 3-4, пересекаясь, дают точку N (N₁, N₂), а прямые 5-6 и 7-8 – точку N' (N'₁, N'₂). Прямая NN' (N₁N₁', N₂N₂') – искомая линия пересечения плоскостей.

Рис. 60 Рис. 61

Рассмотрим построение линии пересечения плоскостей P и Г, с использованием профильной плоскости проекций и без нее. Заданные плоскости являются профильно-проецирующими, а значит линия их пересеченияn параллельна оси х и тоже является профильно-проецирующей прямой (рис. 62). Чтобы найти эту прямую, надо построить одну принадлежащую ей точку. В качестве вспомогательной плоскости можно использовать профильную плоскость проекций (рис. 63, а). Линия n проходит через точку N пересечения следов P_П3 и Г_П3.

Если не применять профильную плоскость проекций, то можно ввести вспомогательную плоскость Σ  П₁ (рис. 63, б) и построить линии пересечения ее с плоскостями P (1- 2) и Г (3- 4). Эти линии, пересекаясь дают искомую точку N (N₁, N₂), общую для плоскостей P и Г. Через N₁ и N₂ проводим проекции прямой n₁ и n₂ параллельно оси х.

а) б)

Рис. 63

В качестве вспомогательных плоскостей для построения линий пересечения двух плоскостей можно использовать плоскости частного положения, которые проводят через прямые, принадлежащие плоскости (рис. 64).

Н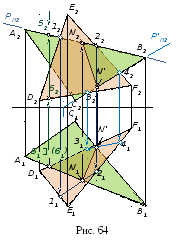а рис. 64 обе точки для обеих плоскостей найдены как точки пересечения (N и N') сторон треугольника АВ и ВС с плоскостью, заданной треугольником DEF. Через прямую АВ проводят фронтально проецирующую плоскость Р, задав её следом P_П2. Она пересекает плоскость треугольника DEF по прямой 1-2 (1₁2₁, 1₂-2₂), которая пересекается со стороной АВ в точке N (N₁, N₂). Фронтально проецирующая плоскость Р', проведенная через прямую ВС, задана следом Р'_П2. Эта плоскость пересекает плоскость треугольника DEF по линии 3-4 (3₁4₁,3₂-4₂), которая в пересечении со стороной ВС дает точку N' (N'₁, N'₂). NN' – искомая линия пересечения плоскостей.

Для определения видимости плоскостей при взаимном их пересечении взяты горизонтально проецирующие точки 5 и 6. Точка 5 принадлежит прямой АВ, а 6 – прямой DF. Анализ положения этих точек показывает, что на П₁ точка 5 закрывает точку 6, а это значит, что прямая АВ в этом месте проходит над DF, т.е. треугольник АВС виден до прямой NN'. Аналогично определяется видимость на фронтальной проекции.