Лекция № 7 взаимное пересечение геометрических образов

1. Общие сведения. 2. Построение линии пересечения двух многогранников. 3. Построение линии пересечения многогранника и кривой поверхности. 4. Построение линии пересечения кривых поверхностей. Метод секущих плоскостей. 5. Метод секущих сфер. 6. Особые случаи пересечения поверхностей.

1 Общие сведения

Форма большинства сложных и ответственных деталей приборов и машин состоит из сочетания элементарных геометрических поверхностей, которые пересекаются между собой.

Для правильного построения границ этих форм необходимо решить задачу на построение линии пересечения элементарных поверхностей. Перед решением этой задачи необходимо:

1. Определить форму пересекающихся поверхностей.

2. Определить взаимное расположение поверхностей.

3. Определить расположение этих поверхностей относительно плоскостей проекций.

Для определения линии пересечения поверхностей находят ряд точек, принадлежащих одновременно обеим поверхностям, и затем эти точки соединяют в определенной последовательности, соблюдая видимость.

Общим способом нахождения точек линии пересечения являются введение вспомогательных секущих посредников. Вспомогательные секущие посредники выбираются таким образом, чтобы линии, по которым они пересекают заданные поверхности, получались простыми и удобными для построения (прямые, окружности). Выбор вспомогательных посредников определяется видом поверхностей и их относительным расположением. Чаще всего применяют вспомогательные секущие плоскости или сферы.

Когда одна или обе пересекающиеся поверхности проецирующие (прямая призма, прямой цилиндр), вводить вспомогательные секущие посредники не требуется, так как уже имеется одна или две проекции искомой линии пересечения.

Общее правило построения линии пересечения поверхностей:

1. Выбирают вид вспомогательных посредников.

2. Строят линии пересечения вспомогательных секущих посредников с заданными поверхностями.

3. Находят точки пересечения построенных линий и соединяют между собой.

При построении точек линии пересечения поверхностей в первую очередь находят характерные (опорные) точки – самые высокие и самые низкие точки по отношению к плоскости П₁; ближайшие и наиболее удаленные по отношению к плоскости П₂; точки на очерковых линиях поверхности – точки отделяющие видимую часть проекции линии от невидимой.

2 Построение линии пересечения двух многогранников

Линией пересечения двух многогранников является пространственная или плоская ломаная линия. Для построения этой линии находят все вершины ломаной и соединяют их, соблюдая видимость.

В рассматриваемом случае (рис. 78) одна из пересекающихся поверхностей проецирующая (призма). Поэтому на чертеже сразу имеется фронтальная проекция линии пересечения. Для построения недостающих проекций линии пересечения необходимо взять точки на пересечении ребер с гранями и ребрами двух многогранников и найти их по правилу принадлежности точек поверхности.

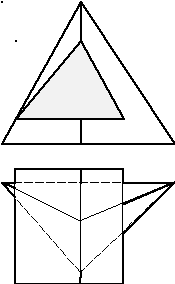?Построить три проекции линии пересечения многогранников.

Рис. 78