Сечение сферы

Плоскость пересекает сферу всегда по окружности, которая может проецироваться на плоскость в виде эллипса,окружностиилиотрезкапрямой линии (рис. 70).

Плоскость	Вид сечения
	на П1	на П3
P	окружность радиусом R	отрезок прямой
Σ	отрезок прямой	окружность радиусом R'
Ω	эллипс	эллипс

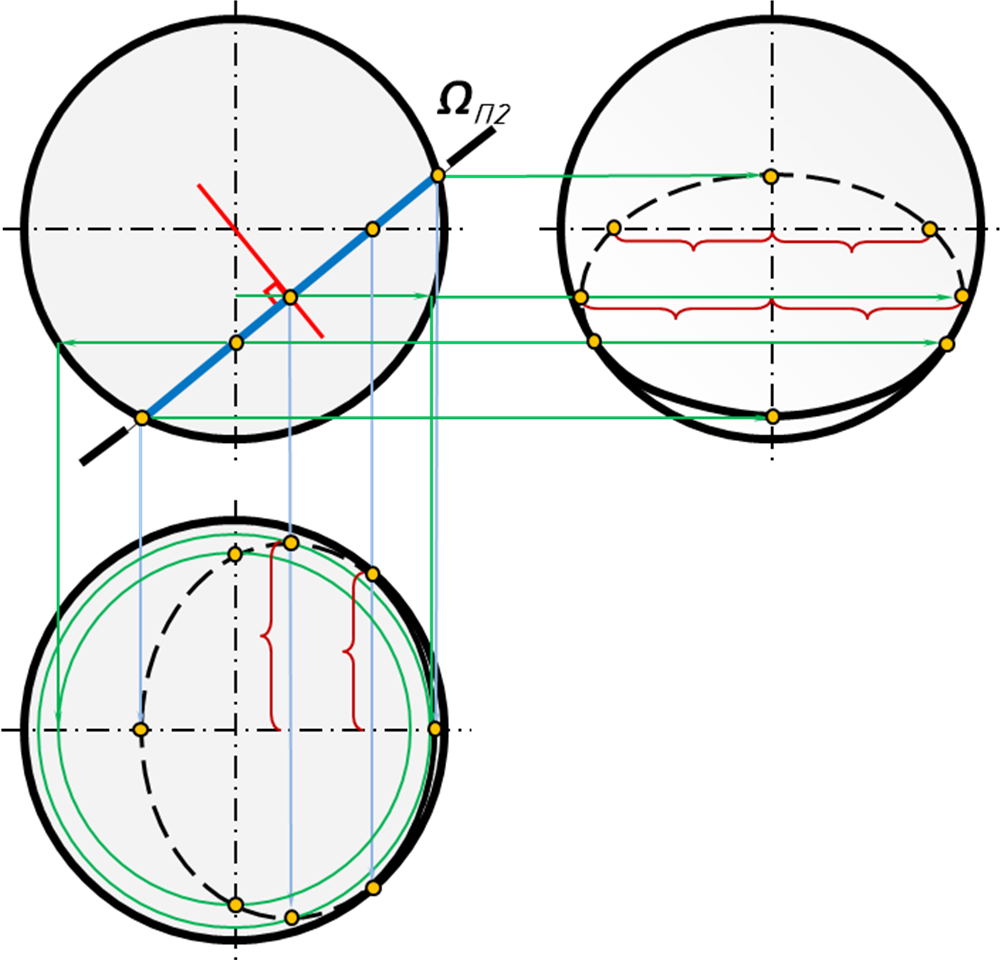
Сечение сферы проецирующей плоскостью Ω  П₂

Окружность сечения проецируется на фронтальную плоскость в отрезок прямой линии С₂ D₂, а на горизонтальную плоскость проекций в эллипс, большая ось которого равна диаметру окружности сечения.

Для построения большой оси А₁В₁ (горизонтальной проекции, определяем середину отрезкаС₂ D₂, через точку (А₂В₂) проводится параллель, находят горизонтальную проекцию этой параллели и по линиям связи определяют на ней точки осиА₁иВ_1.

Точки 1 и 1, расположенные на экваторе, являются границей видимости на П₁. Точки 2 и 2, расположенные на главном меридиане, являются границей видимости на П₃.

Лекция № 6 аксонометрические проекции

1. Общие сведения. 2. Показатели искажения. 3. Виды аксонометрических проекций. 4. Построение окружности в аксонометрии.

1 Общие сведения

При выполнении технических чертежей часто бывает необходимым иметь более наглядные изображения предметов. Для построения таких изображений применяют аксонометрические проекции (аксонометрию).

Аксонометрия – греческое слово, сос­тоящее из двух слов ахсоn – ось и metreo – измеряю.

Способ аксонометрического проецирования состоит в том, что предмет вместе с осями коор­динат, к которым он отнесен в пространстве, проецируется на какую-либо плос­кость параллельными лучами. Эта плоскость называется плоскостью аксонометрических проекций или картинной плоскостью (рис. 71).

Направление проецирования не должно совпадать ни с одной из осей координат, тогда и изображение получается наглядным.

Кроме наглядности аксонометрические проекции допускают и измерение предмета по трем координатным направлениям.

Построение изображения предмета выполняется по каркасу характерных для предмета точек с учетом свойств параллельного проецирования: параллельные прямые остаются на аксонометрических проекциях параллельными, точки, принадлежащие линиям, на проекциях принадлежат аксонометрическим проекциям этих линий. Все измерения делаются только по осям или параллельно осям.Характерные точки строятся по координатам.

К – аксонометрическая (картинная) плоскость;

S– направление проецирования.

2 Показатели искажения

Для возможности использования метода координат в аксонометрии вводятся показатели искажения по осям.

На рис. 72 изображена пространственная система координат, единичные отрезки е на осях координат и их проекция в направлении S на некоторую плоскость К, являющуюся аксонометрической плос­костью проекций. Проекции е_х, е_у, e_z отрезка е на соответствующих аксонометрических осях в общем случае не равны отрезкуе и не равны между собой. Отрезкие_х, е_у, e_z являютсяединицами измерения по аксонометрическим осям — аксоно­метрическими единицами (аксонометрическими масштабами).

Отношение длинны отреза в аксонометрических проекциях к истинной длине отрезка называют показателем искажения (коэффициентом искажения):

.

Зная величину коэффициента искажения можно построить аксонометрическое изображение точки по ее натуральным координатам, пользуясь следующими формулами:

Х₁= К_х  Х; У₁= К_у  У;

Z₁= К_z  Z .

Показатели искажения связаны между собой соотношениями:

в прямоугольной аксонометрии:

К_х²  К_у²  К_z ² = 2,

в косоугольной аксонометрии:

К_х²  К_у²  К_z ² = 2  сtg².