
Индивидуальное задание №1
(ЛИНЕЙНАЯ АЛГЕБРА. Задания №1,2)
Задание 1. Вариант 1
-
Вычислить определители:
![]() ;
;
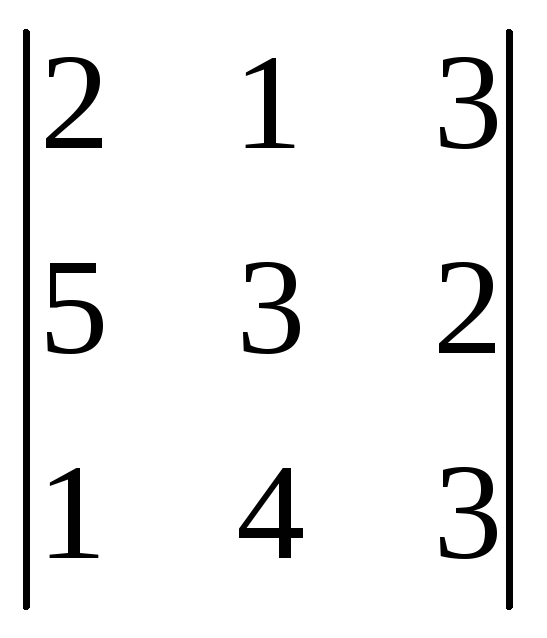 ;
;
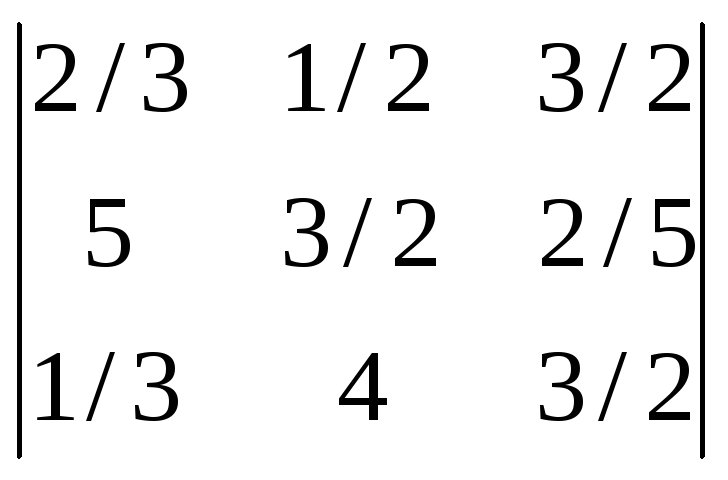
-
Пользуясь свойствами определителей, вычислить:
 ;
;
-
Пользуясь теоремой Лапласа, вычислить определители:
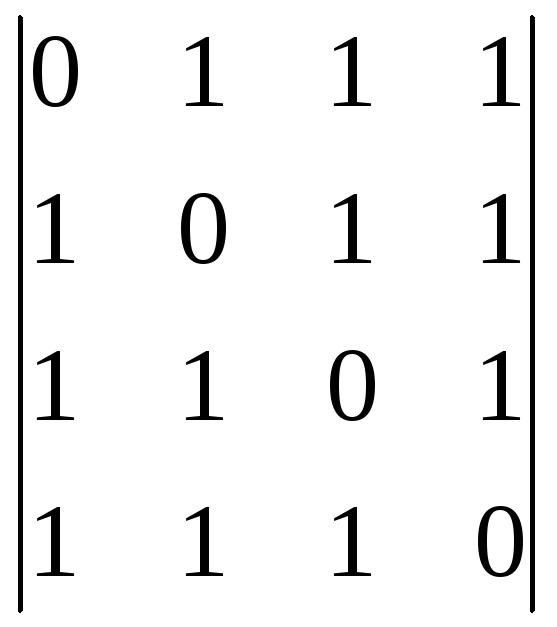
-
Вычислить произведение матриц:
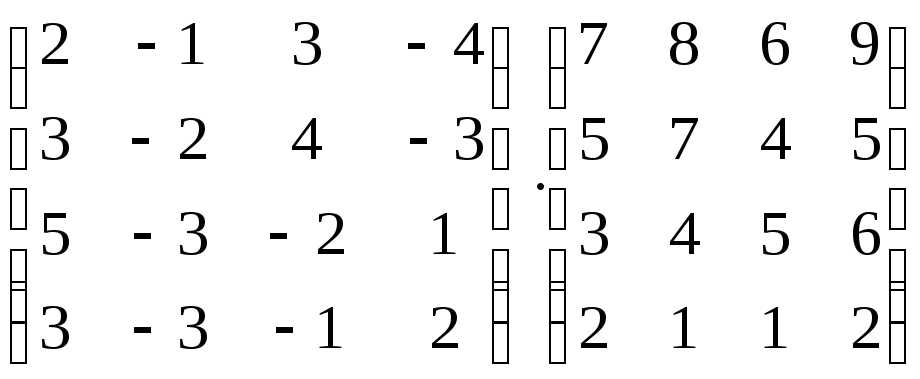
-
Вычислить выражение:
![]()
-
Решить матричные уравнения:
![]()
-
Как изменится произведение АВ матриц
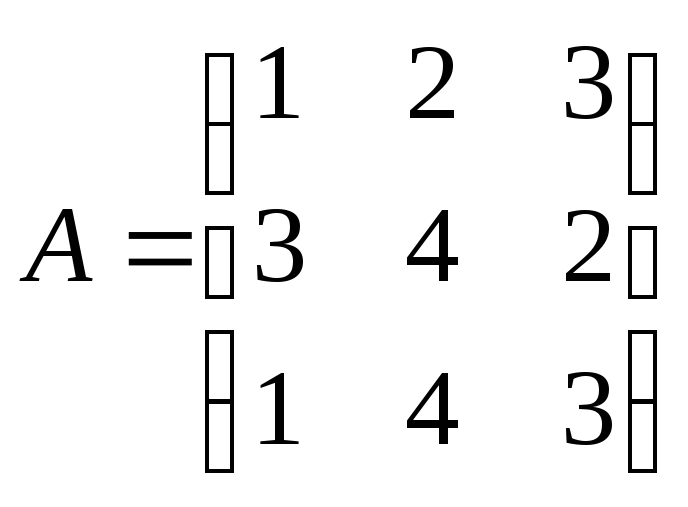 и
и
 ,
если переставить местами 1-ую и 2-ую
строки матрицы А
?
,
если переставить местами 1-ую и 2-ую
строки матрицы А
?
Вариант 2
-
Вычислить определители:
![]() ;
;
![]() ;
;
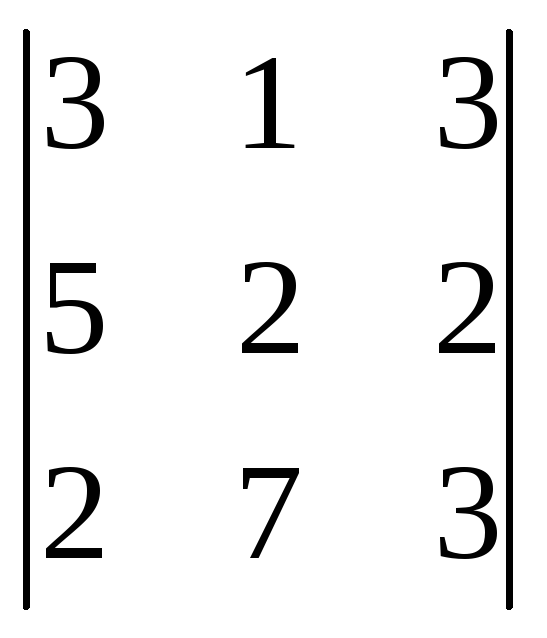 ;
;
-
Пользуясь свойствами определителей, вычислить:
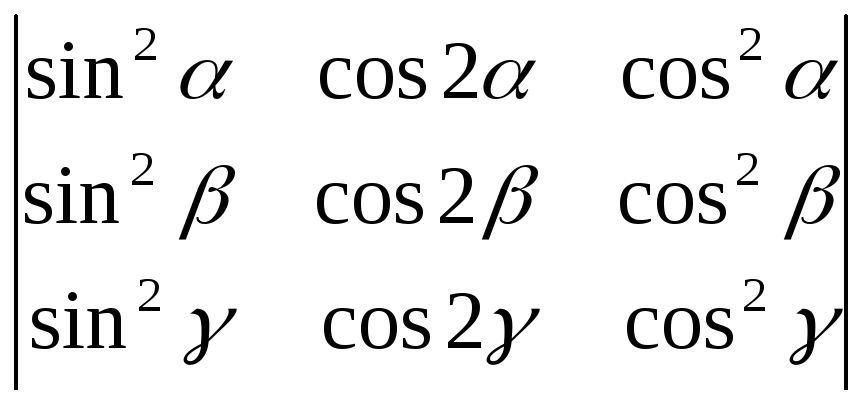 ;
;
-
Пользуясь теоремой Лапласа, вычислить определители:
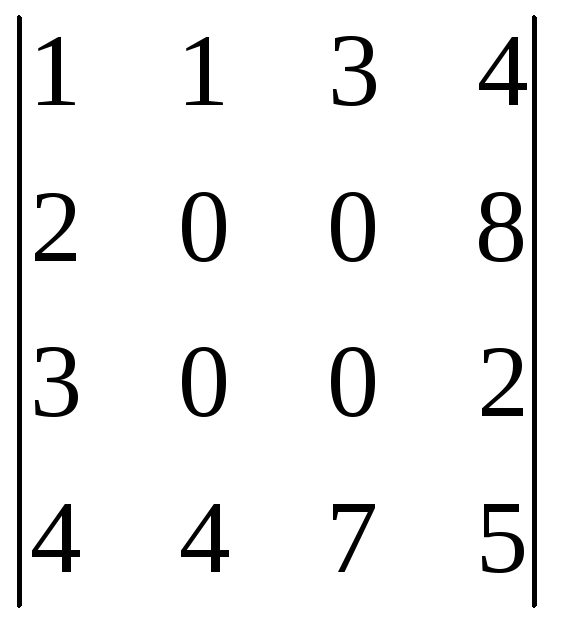 ;.
;.
-
Вычислить произведение матриц:
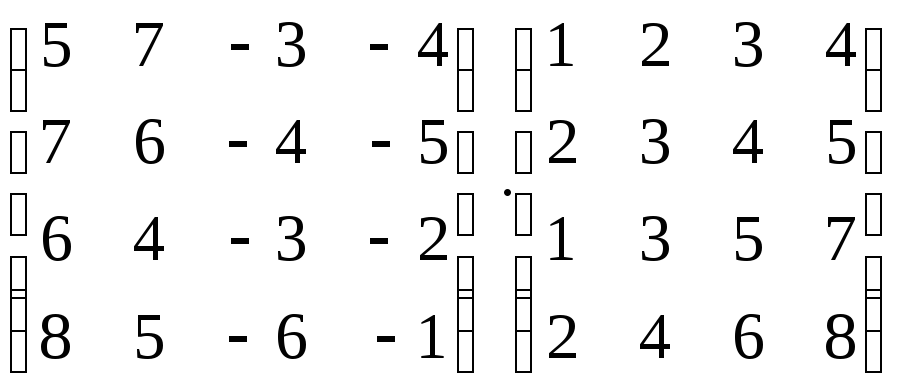
-
Вычислить выражение:
![]()
-
Решить матричные уравнения:
![]()
-
Как изменится произведение АВ матриц
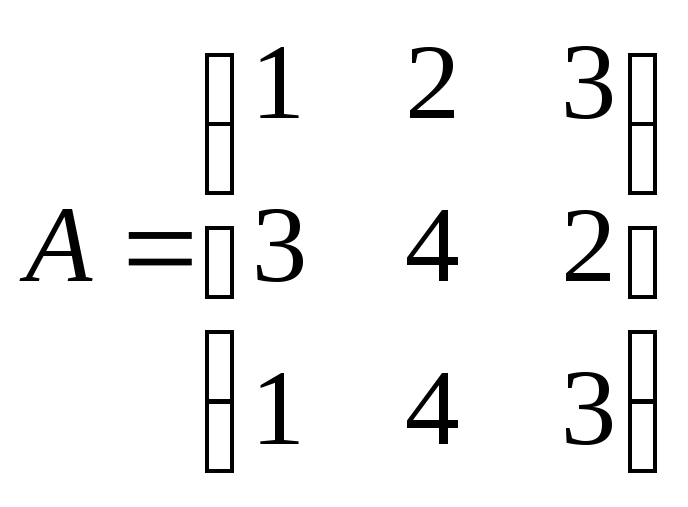 и
и
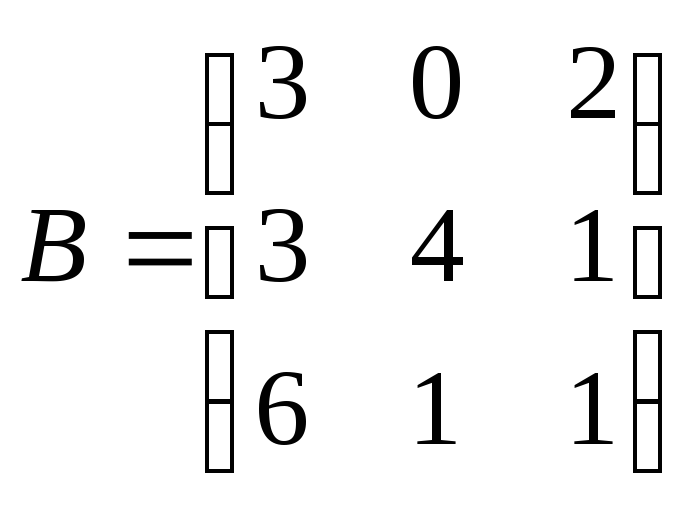 ,
если переставить местами 1-ую и 3-ую
строки матрицы А
?
,
если переставить местами 1-ую и 3-ую
строки матрицы А
?
Вариант 3
-
Вычислить определители:
![]() ;
;
![]() ;
;
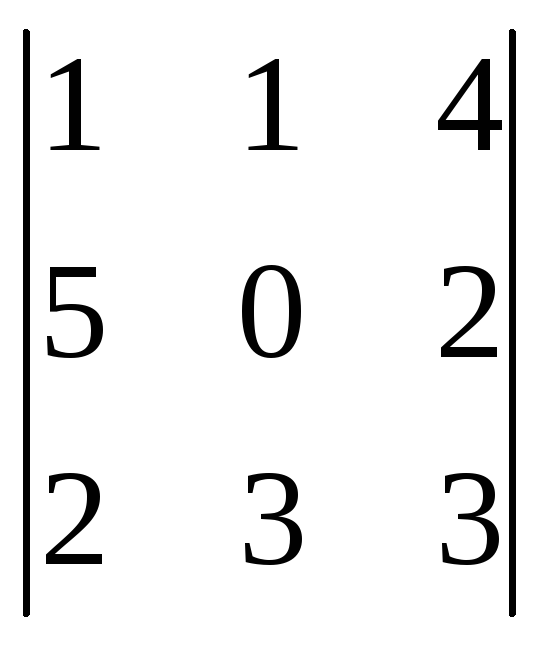 ;
;
-
Пользуясь свойствами определителей, вычислить:
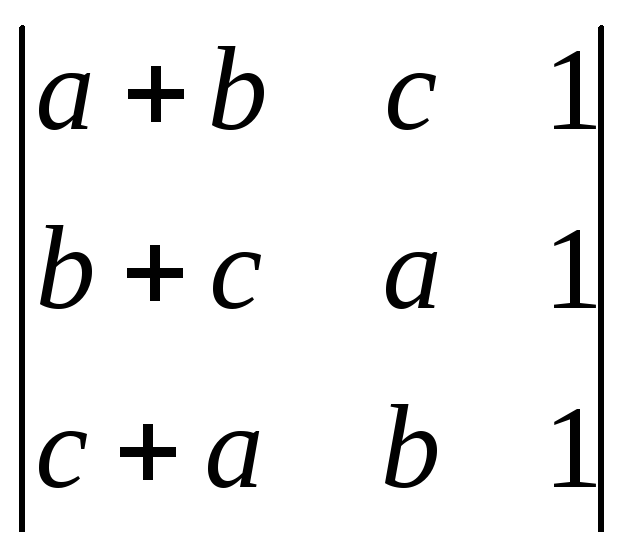 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
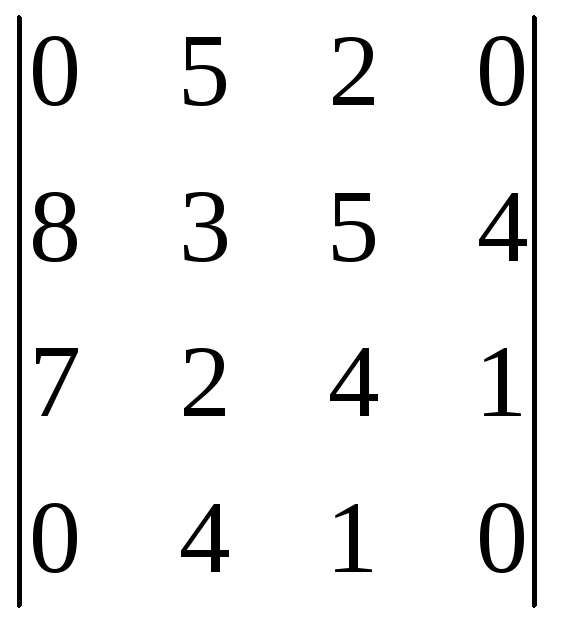 ;
;
-
Вычислить произведение матриц:
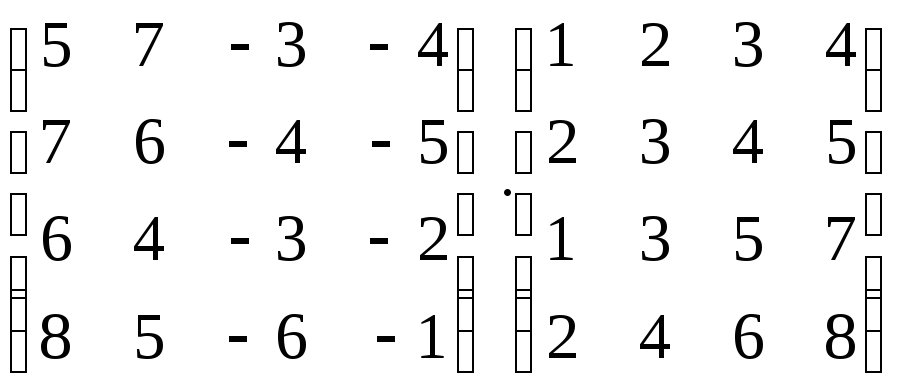
-
Вычислить выражение:
![]()
-
Решить матричные уравнения:
![]()
-
Как изменится произведение АВ матриц
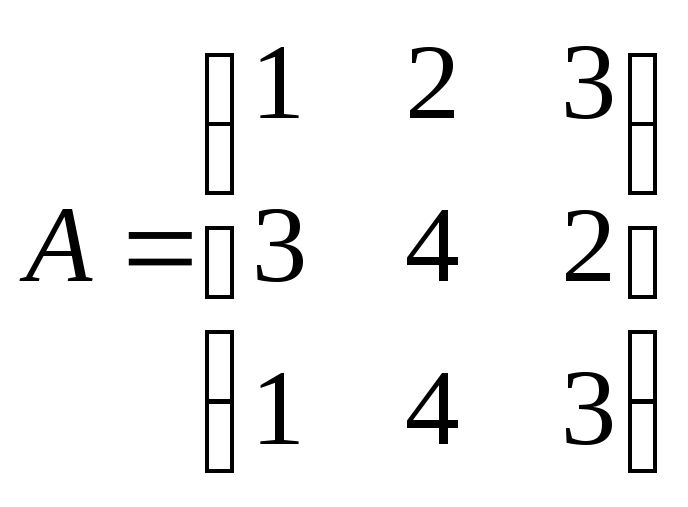 и
и
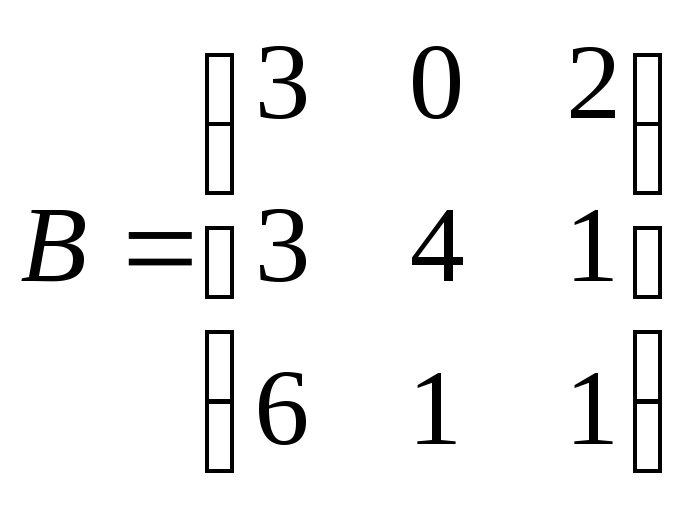 ,
если переставить местами 2-ую и 3-ую
строки матрицы А
?
,
если переставить местами 2-ую и 3-ую
строки матрицы А
?
Вариант 4
-
Вычислить определители:
![]() ;
;
![]() ;
;
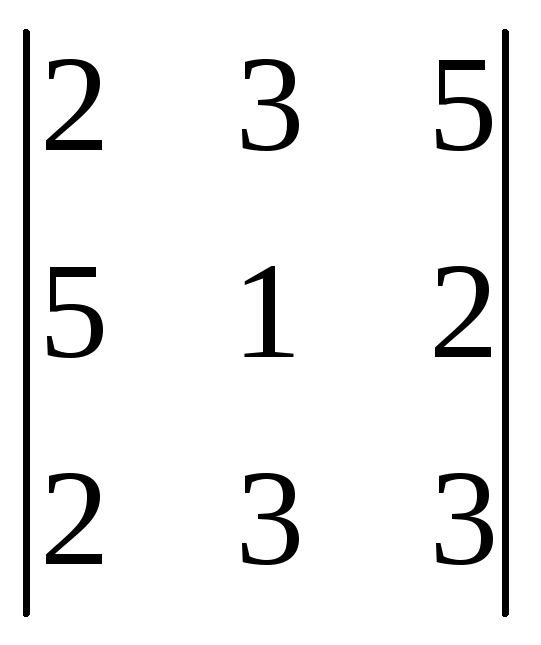 ;
;
-
Пользуясь свойствами определителей, вычислить:
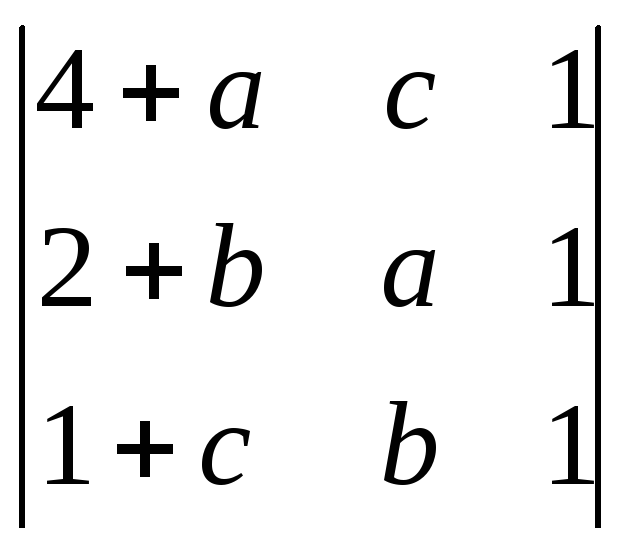 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
 ..
..
-
Вычислить произведение матриц:
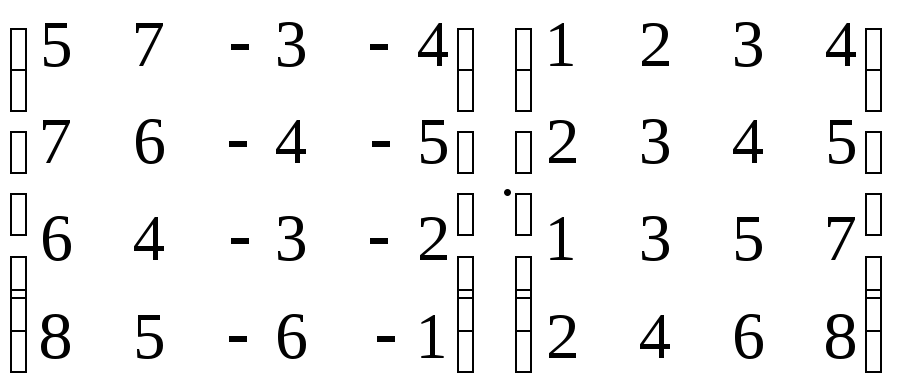
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
![]()
-
Как изменится произведение АВ матриц
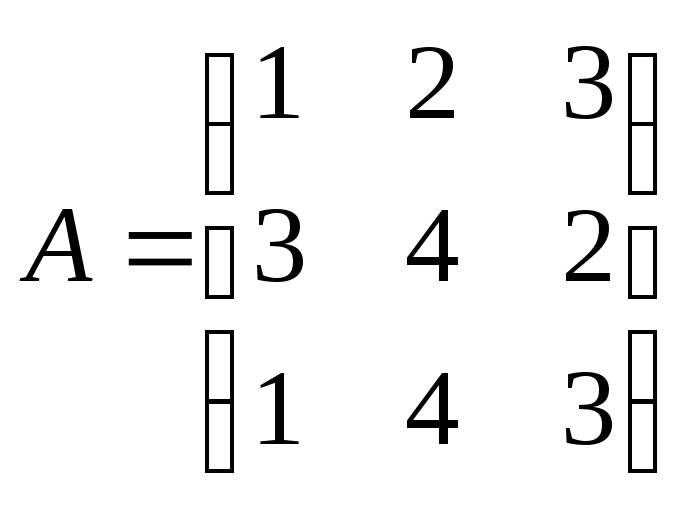 и
и
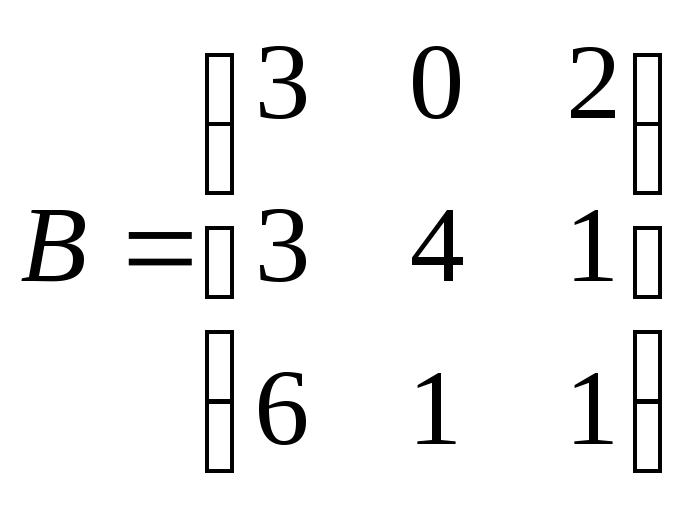 ,
если переставить местами 1-ый и 2-ой
столбцы матрицы А
?
,
если переставить местами 1-ый и 2-ой
столбцы матрицы А
?
Вариант 5
-
Вычислить определители:
![]() ;
;
![]() ;
;
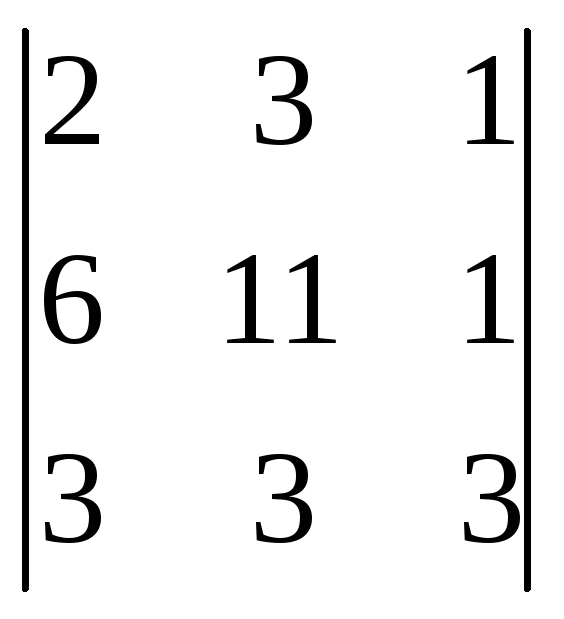 ;
;
-
Пользуясь свойствами определителей, доказать:
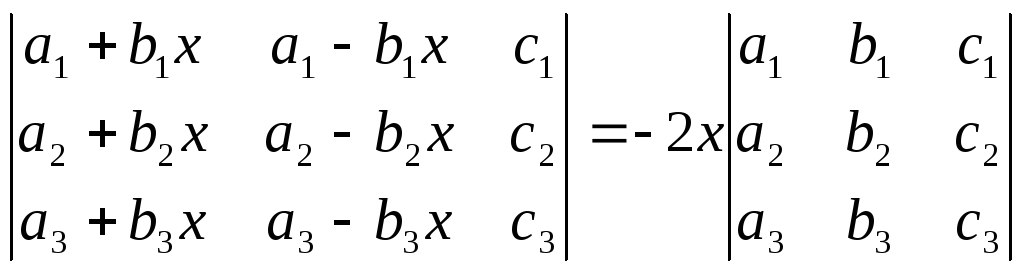 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
 .
.
-
Вычислить произведение матриц:
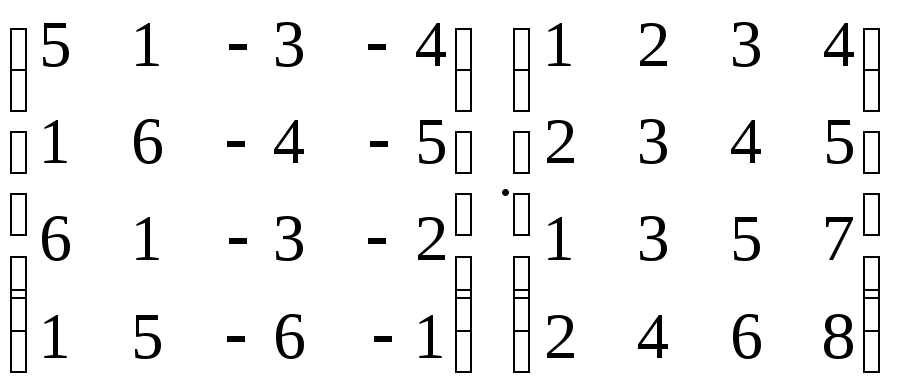 .
.
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
![]()
-
Как изменится произведение АВ матриц
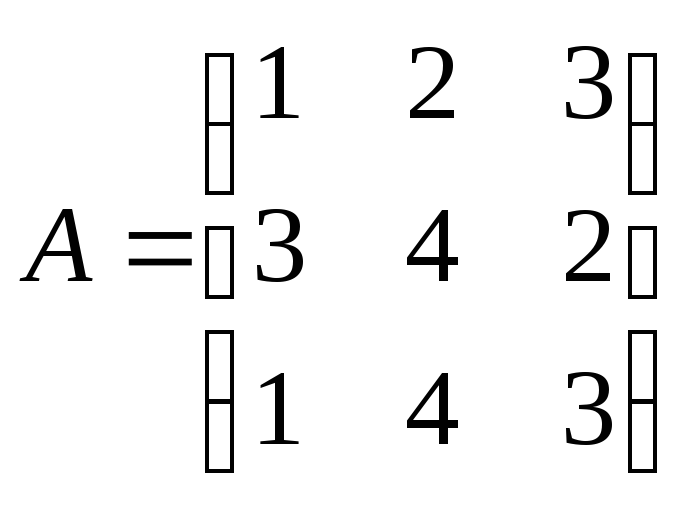 и
и
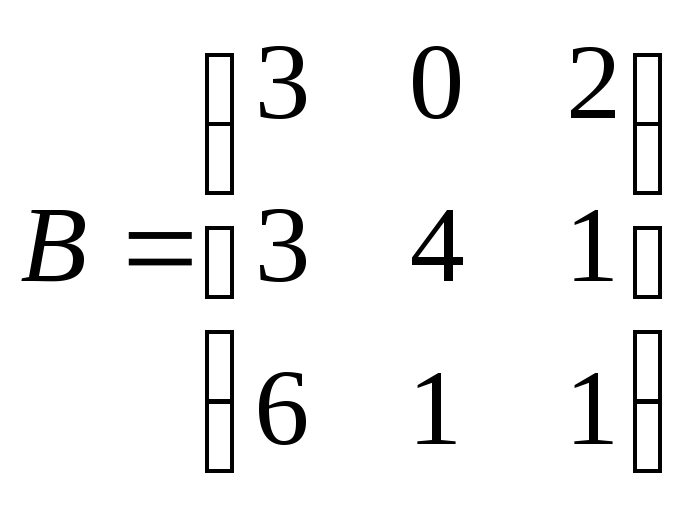 ,
если переставить местами 1-ый и 3-ий
столбцы матрицы А
?
,
если переставить местами 1-ый и 3-ий
столбцы матрицы А
?
Вариант 6
-
Вычислить определители:
![]() ;
;
![]() ;
;
 ;.
;.
-
Пользуясь свойствами определителей, доказать:
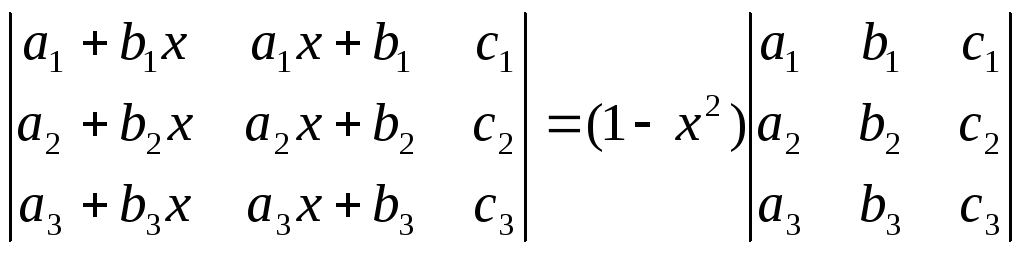 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
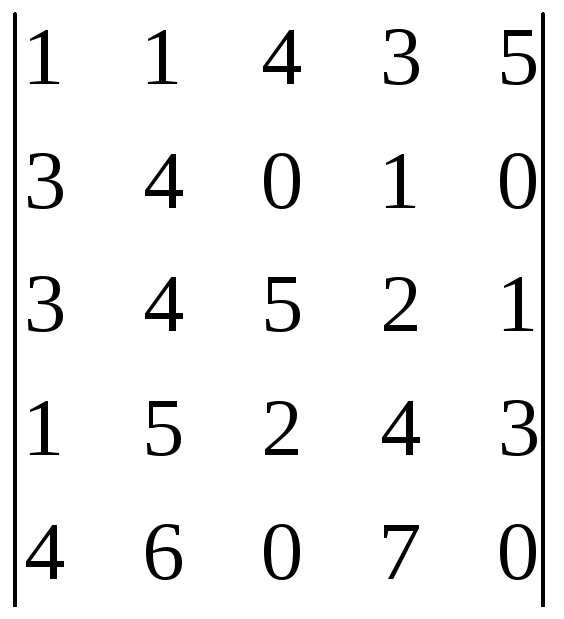 .
.
-
Найти обратную матрицу для матрицы А:
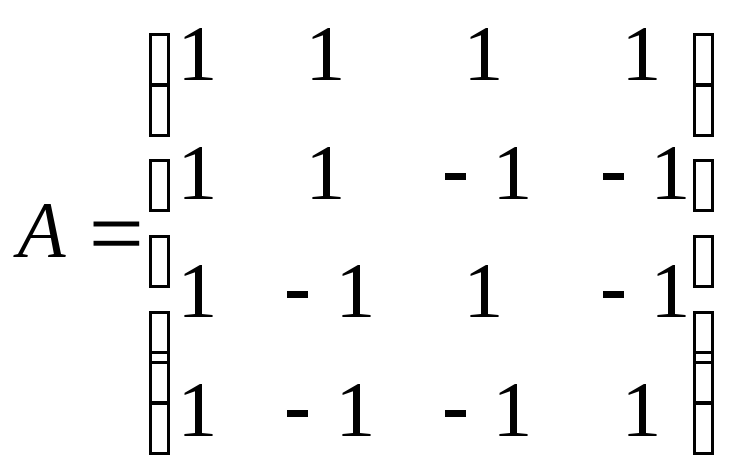 .
.
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
![]()
-
Как изменится произведение АВ матриц
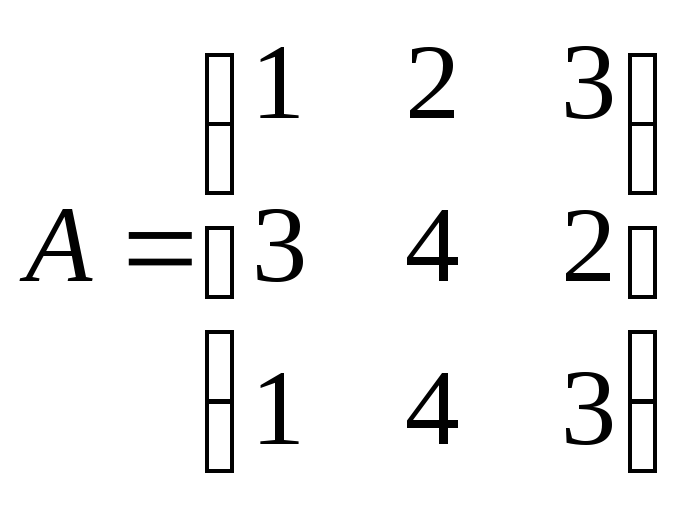 и
и
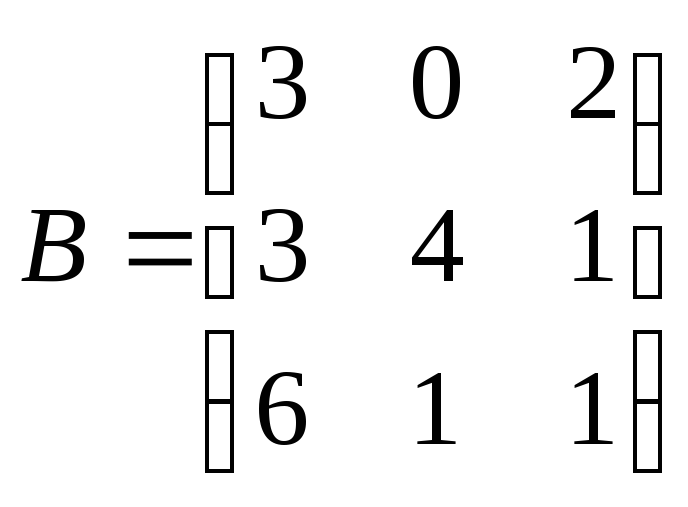 ,
если переставить местами 2-ой и 3-ий
столбцы матрицы А
?
,
если переставить местами 2-ой и 3-ий
столбцы матрицы А
?
Вариант 7
-
Вычислить определители:
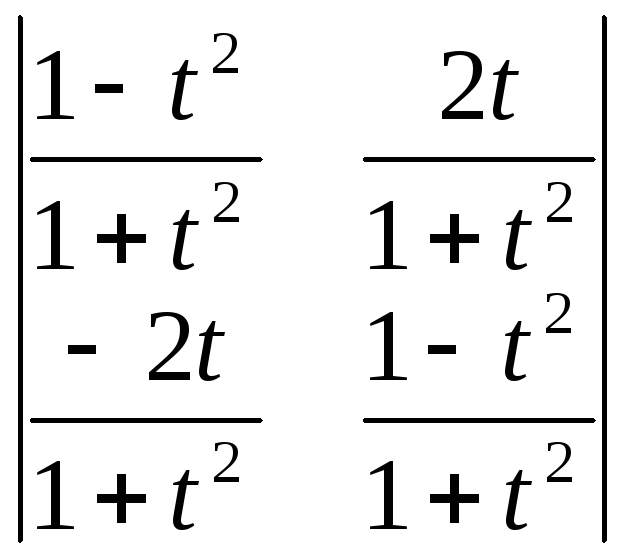 ;
;
 ;.
;.
-
Пользуясь свойствами определителей, доказать:
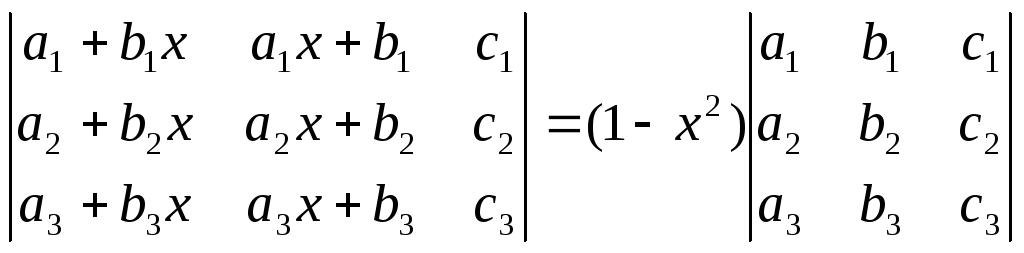 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
 .
.
-
Найти обратную матрицу для матрицы А:
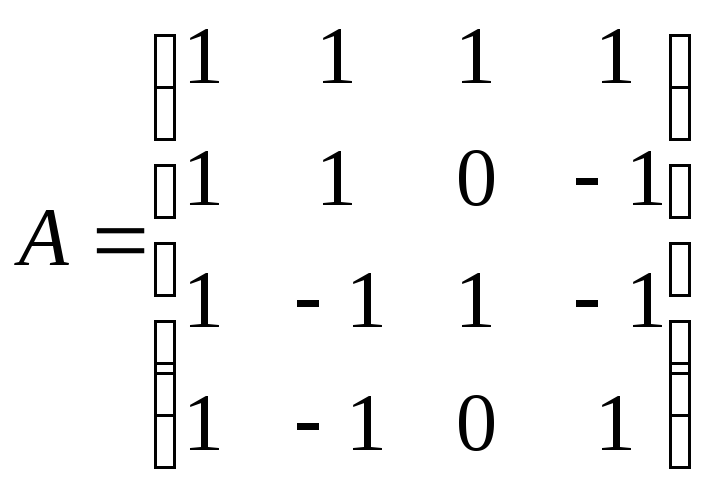 .
.
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
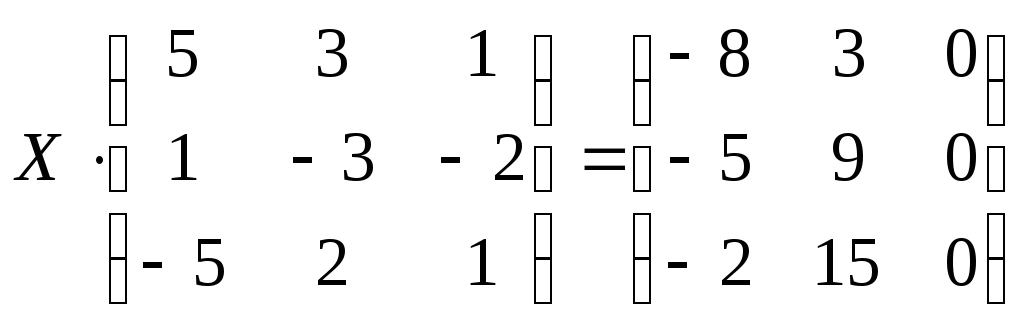
Вариант 8
-
Вычислить определители:
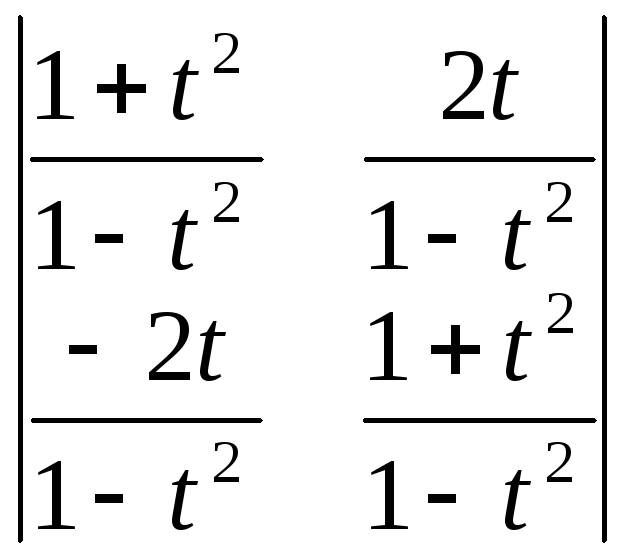 ;
;
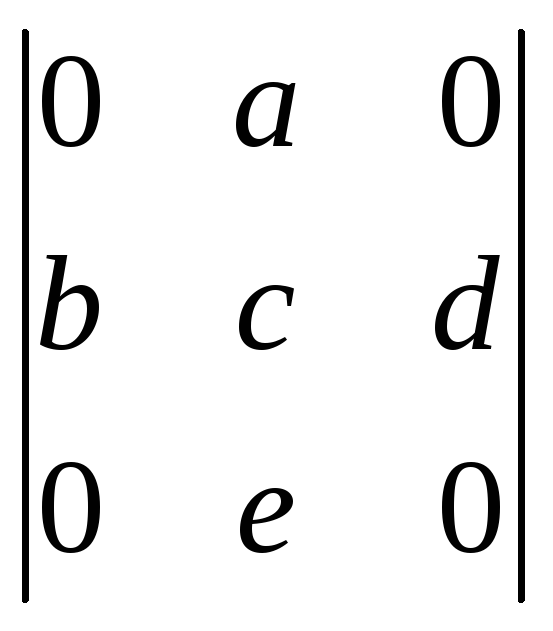 ;
; -
Пользуясь свойствами определителей, доказать:
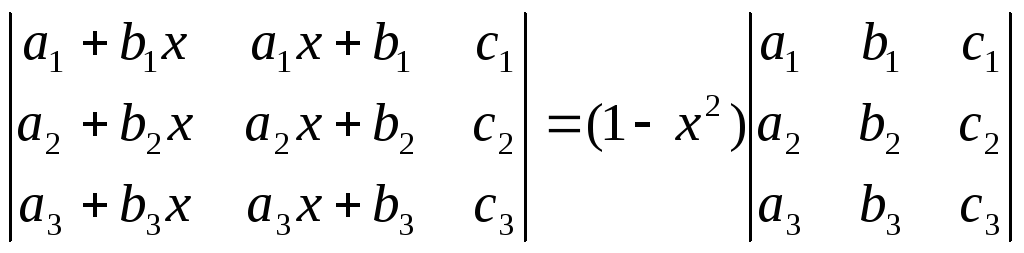 ;
;
-
Пользуясь теоремой Лапласа, вычислить определители:
 .
.
-
Найти обратную матрицу для матрицы А:
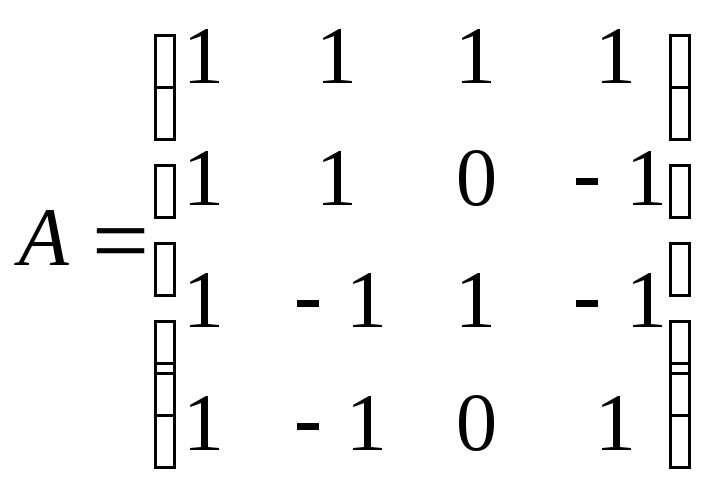 .
.
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
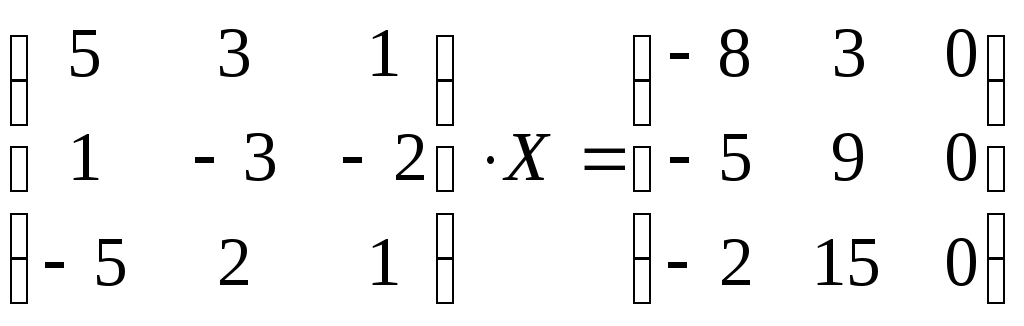 .
.
Вариант 9
-
Вычислить определители:
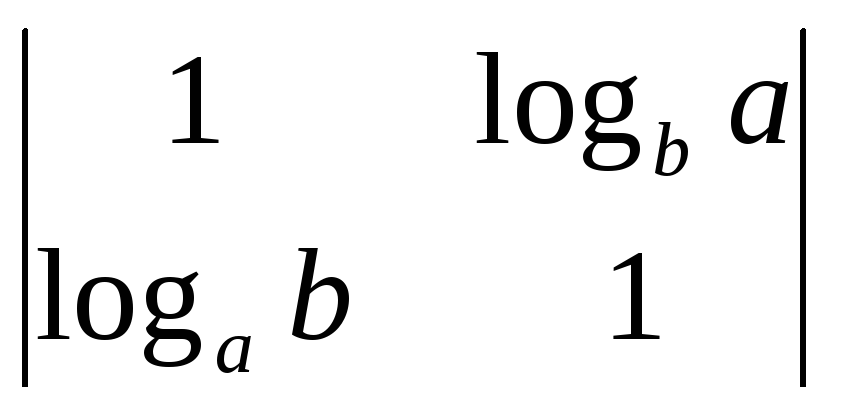 ;
;
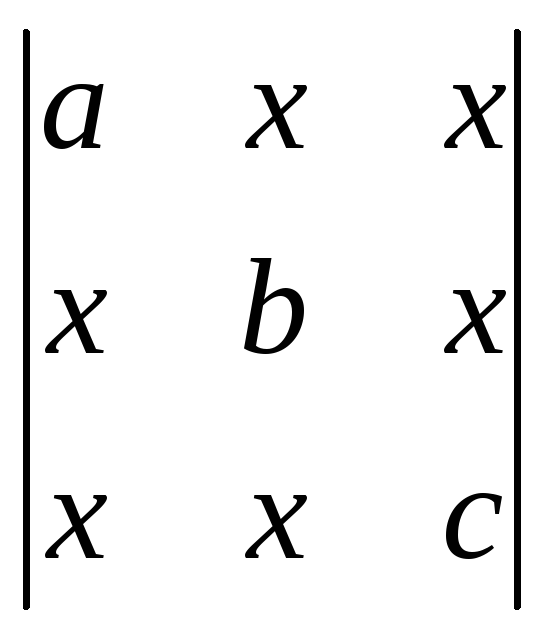 ;
; -
Пользуясь свойствами определителей, доказать:
 ;
;
-
Вычислить определитель:
 .
.
-
Найти обратную матрицу для матрицы А:
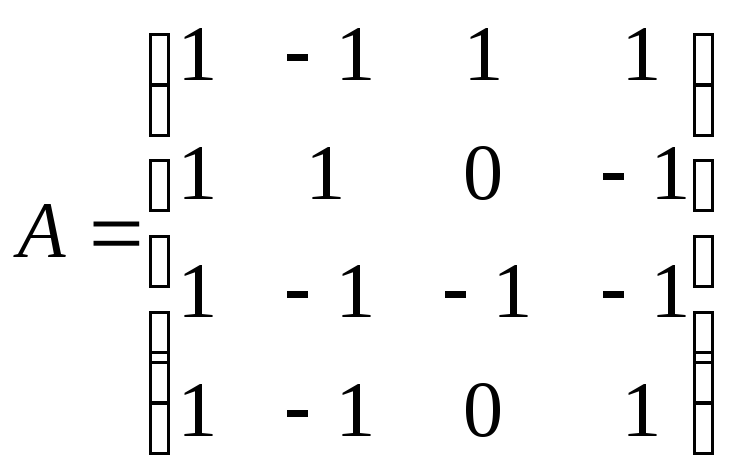 .
.
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
![]() .
.
Вариант 10
-
Вычислить определители:
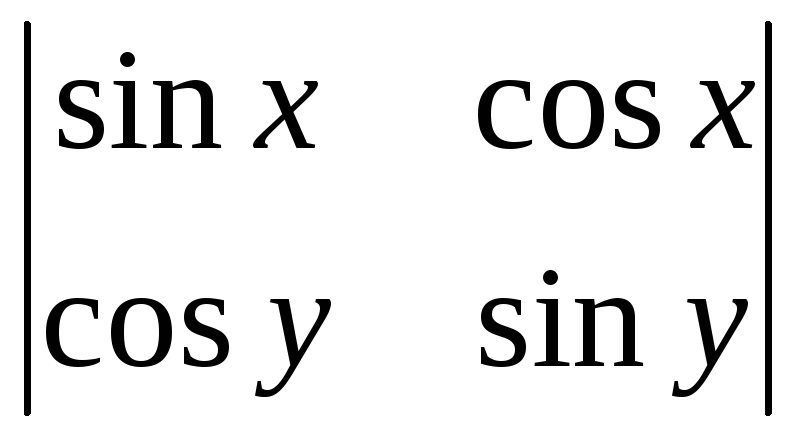 ;
;
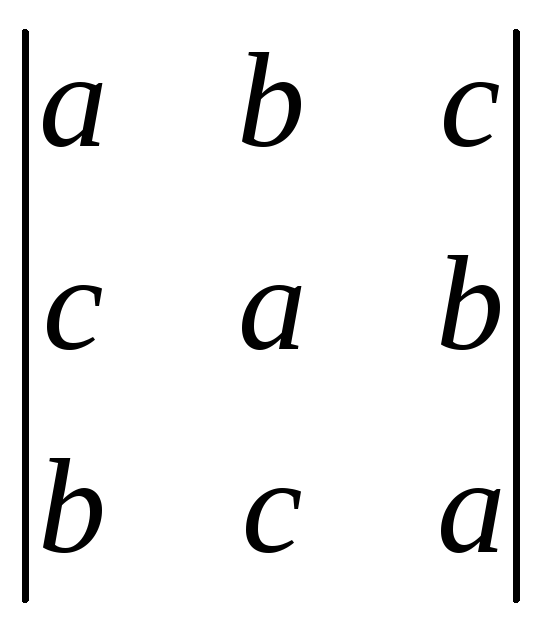 ;.
;. -
Пользуясь свойствами определителей, доказать:
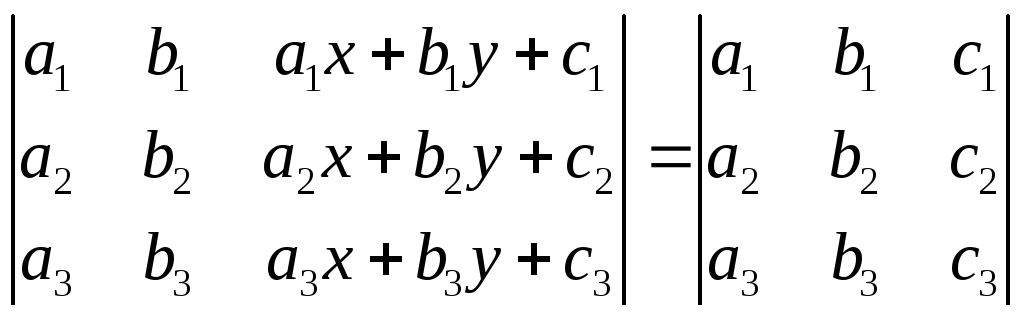 ;
;
-
Вычислить определитель:
 ;
;
-
Найти обратную матрицу для матрицы А:
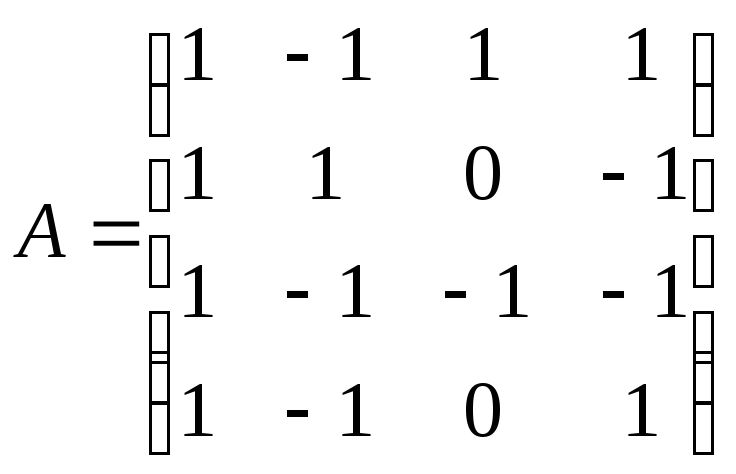 ;
;
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
![]() .
.
Вариант 11
-
Вычислить определители:
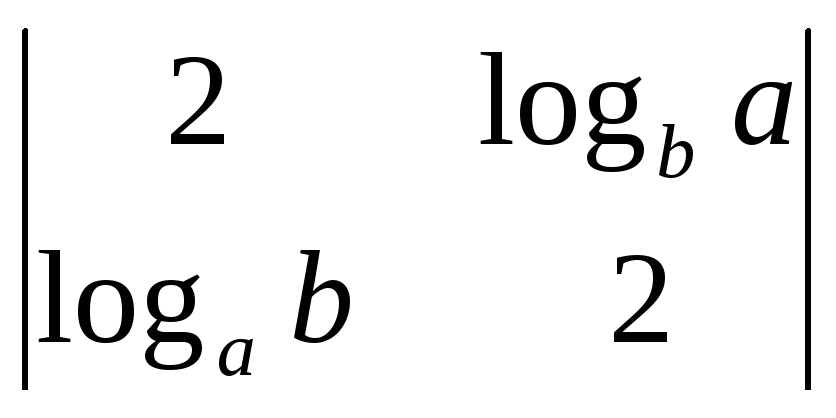 ;
;
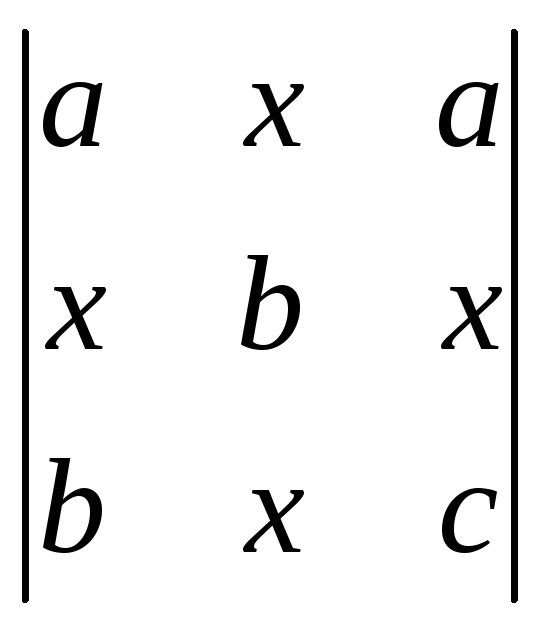 ;
; -
Верно ли равенство:
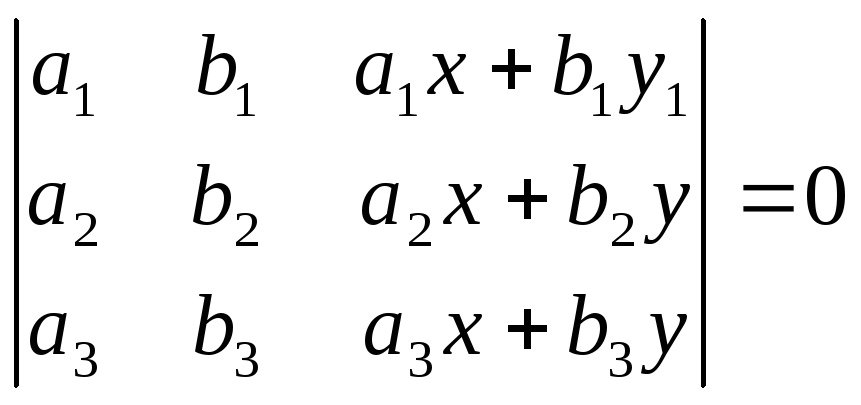 ;
;
-
Вычислить определитель, разложив его по первому столбцу:
 .
.
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
![]() ;
;
-
Найти произведение матриц:
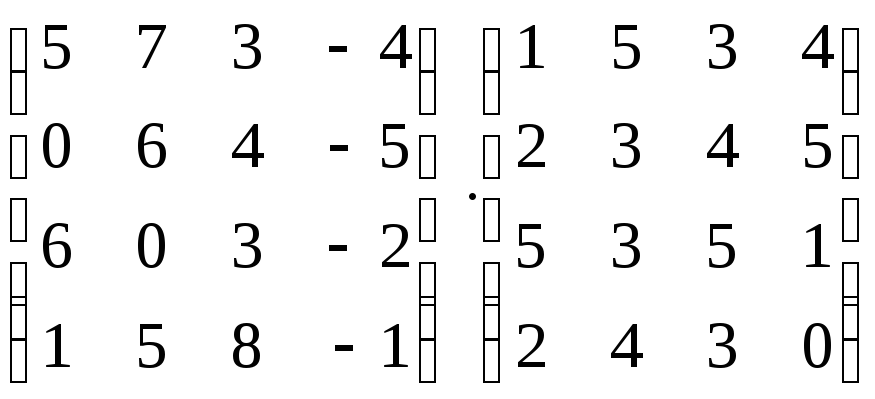 .
.
Вариант 12
-
Вычислить определители:
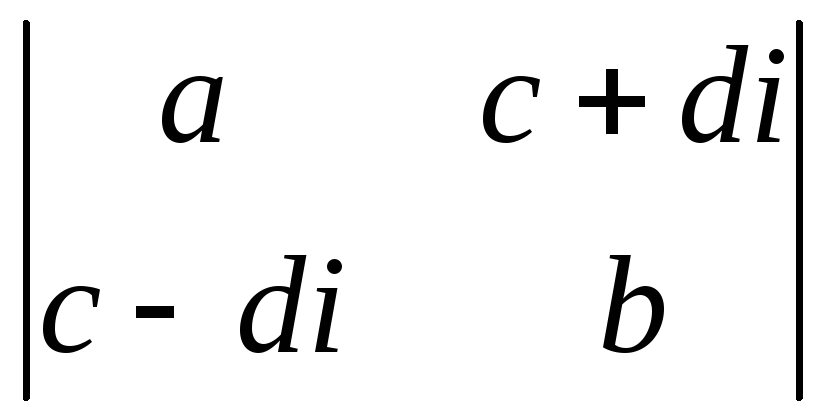 ,
где
,
где
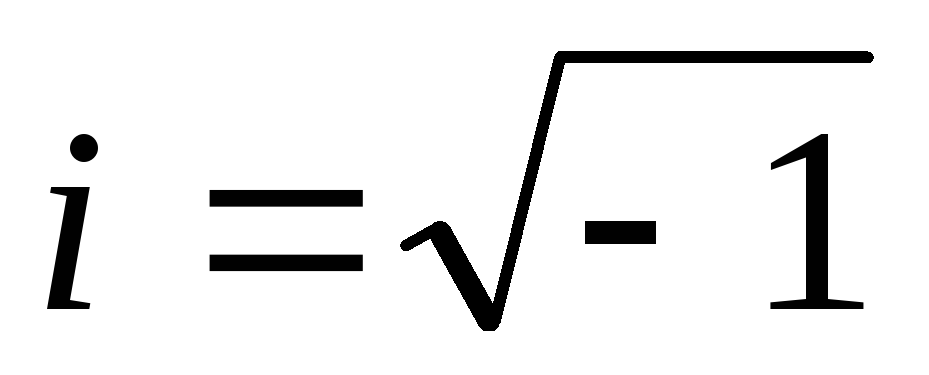 ;
;
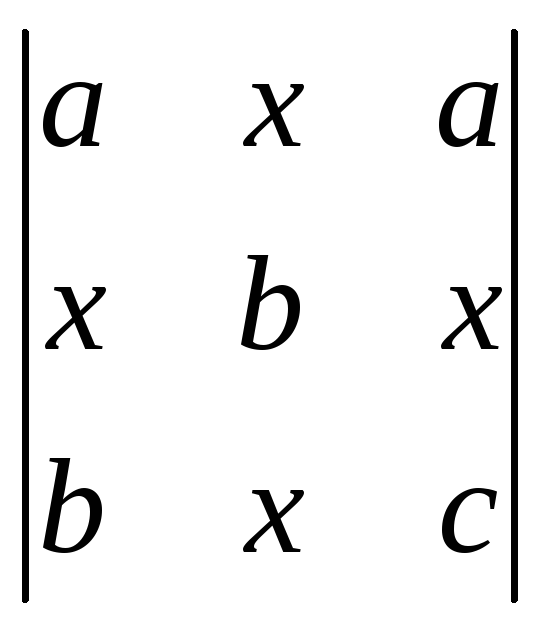 ;
;
-
Верно ли равенство:
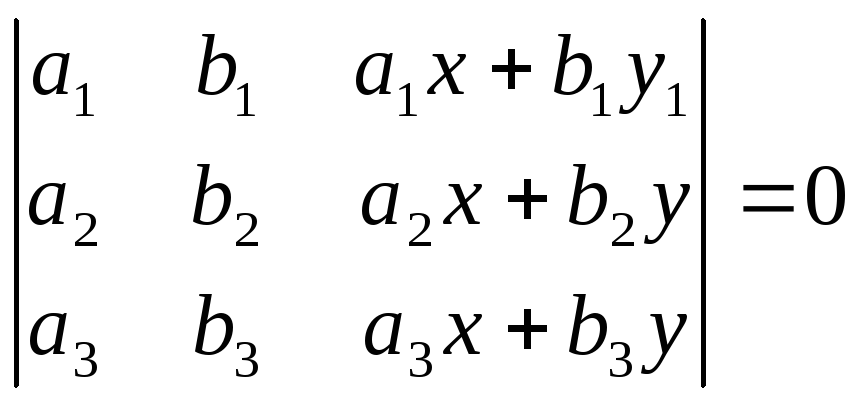 ;
;
-
Вычислить определитель, разложив его по второму столбцу:
 .
.
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
![]()
-
Найти произведение матриц:
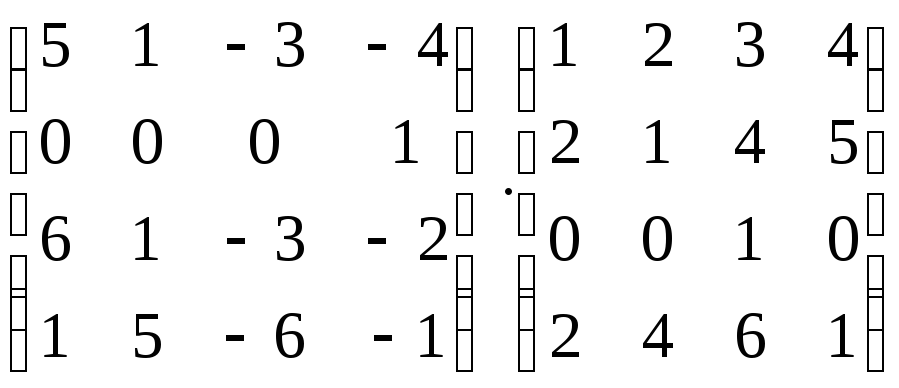
Вариант 13
1) Вычислить
определители: ![]() ,
где
,
где
![]() ;
;
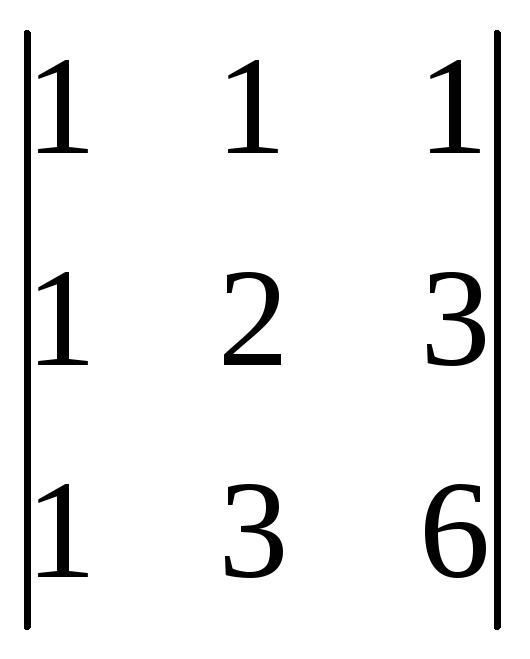 ;
;
2) Верно ли равенство:
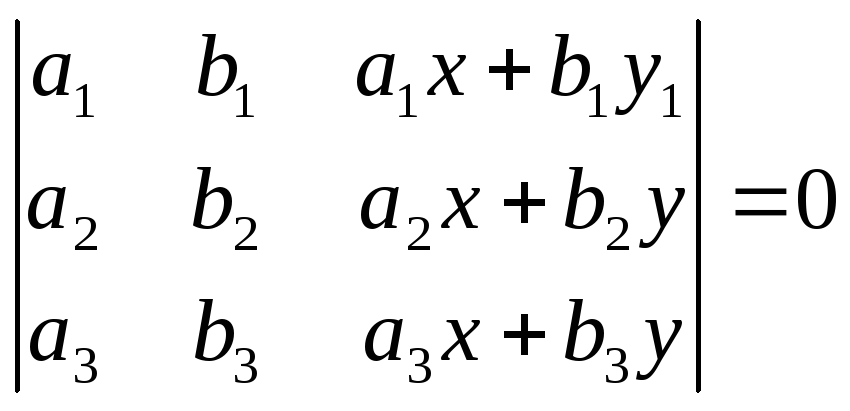 ;
;
3) Вычислить определитель, разложив его по второму столбцу:
 .
.
4) Вычислить выражение:
![]()
5) Решить матричное уравнение:
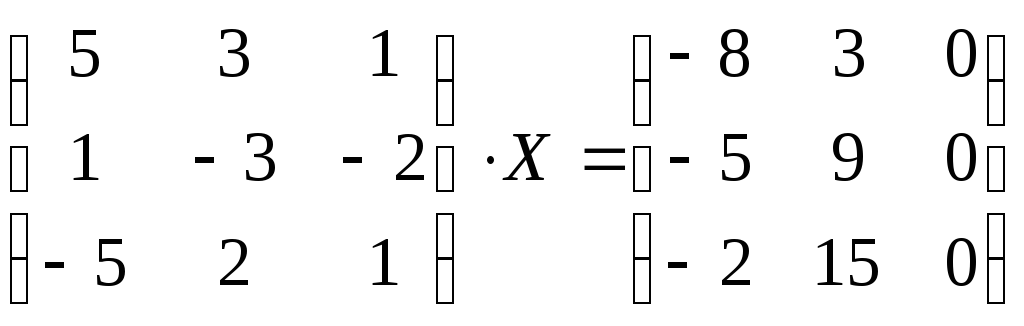 ;
;
6) Найти матрицу
D=AB-C2,
где
![]() ;
;
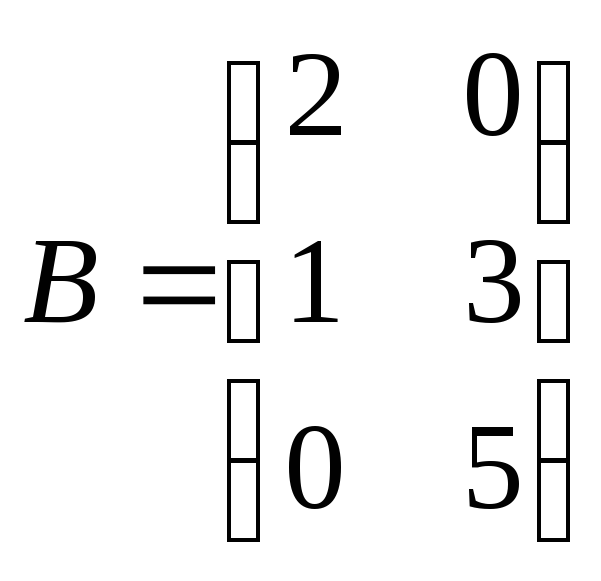 ;
;
![]() .
.
Вариант 14
-
Вычислить определители:
![]() ;
;
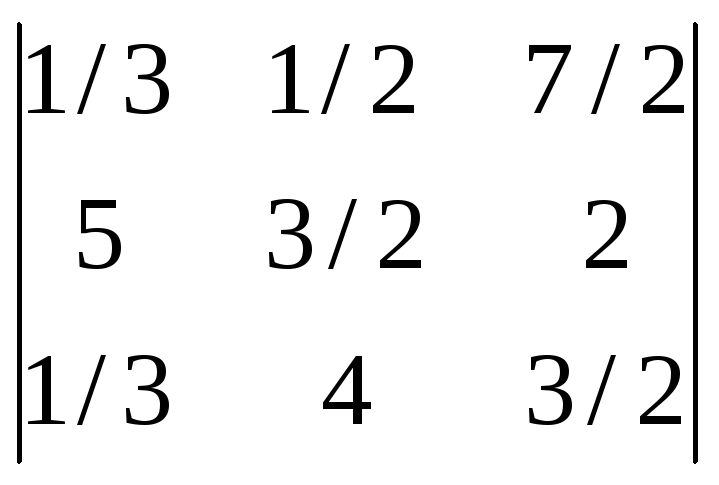
-
Пользуясь свойствами определителей, вычислить:
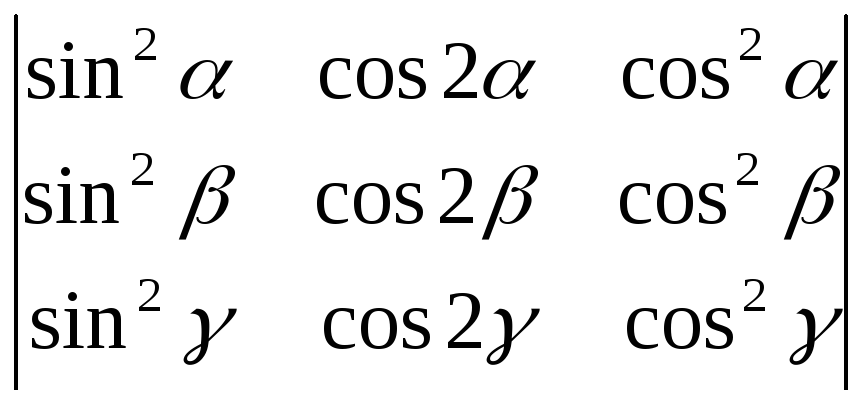 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
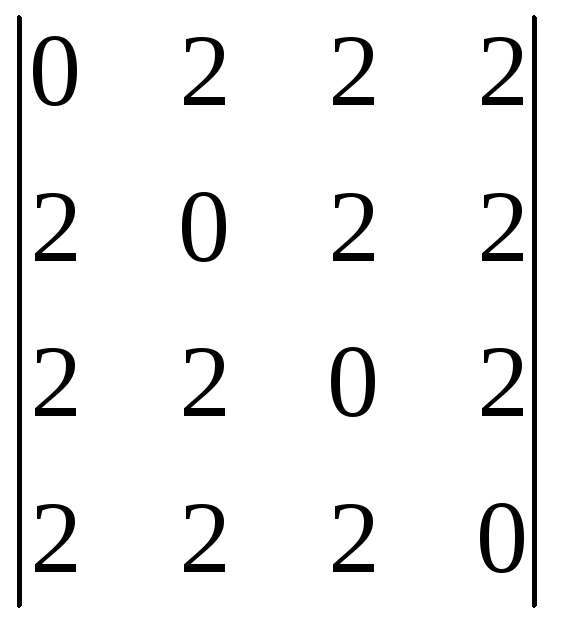 ;
;
-
Вычислить произведение матриц:
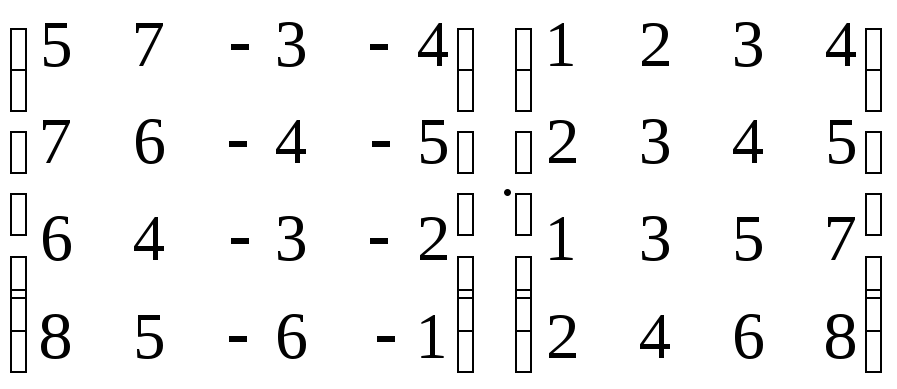
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
![]()
Вариант 15
-
Вычислить определители:
![]() ;
;
![]() ;
;
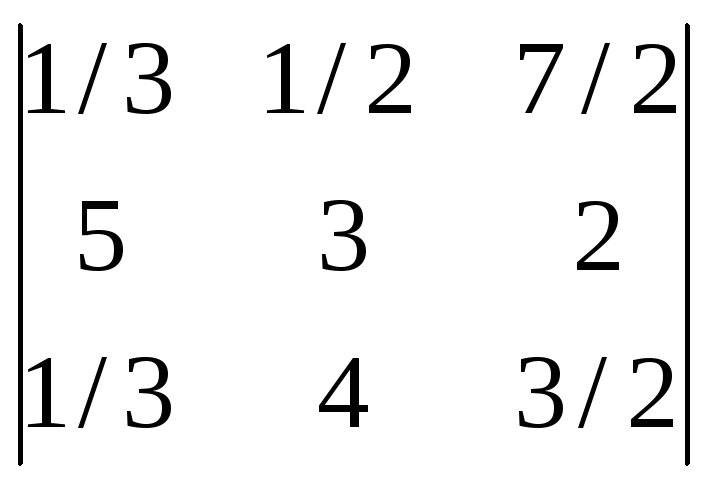
-
Пользуясь свойствами определителей, вычислить:
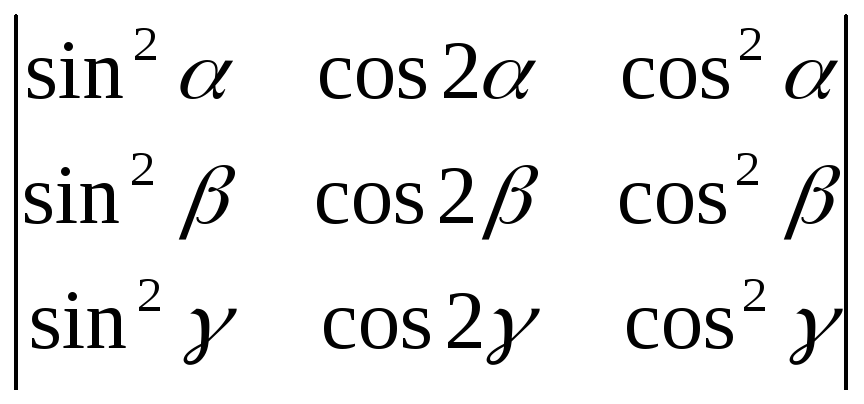 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
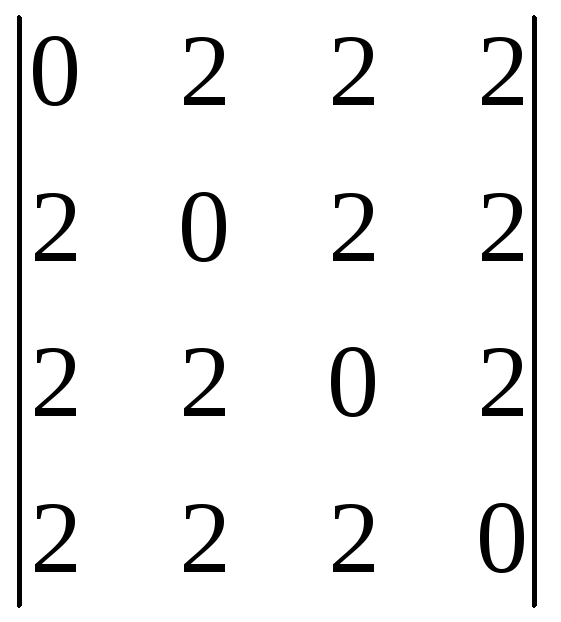 ;
;
-
Вычислить произведение матриц:
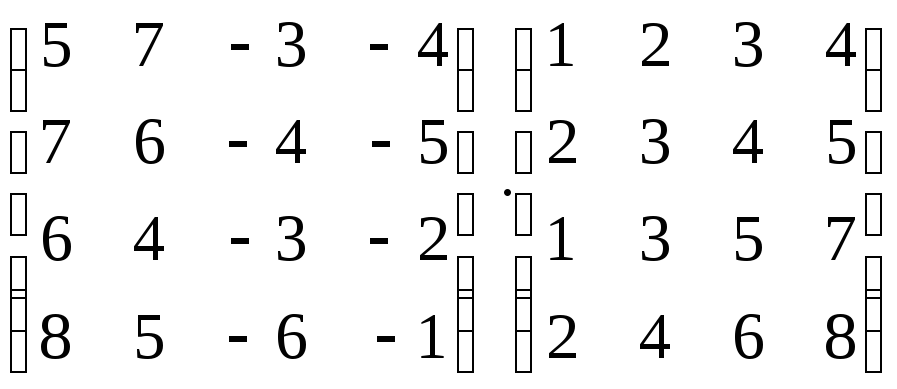
-
Вычислить выражение:
![]()
-
Решить матричное уравнение:
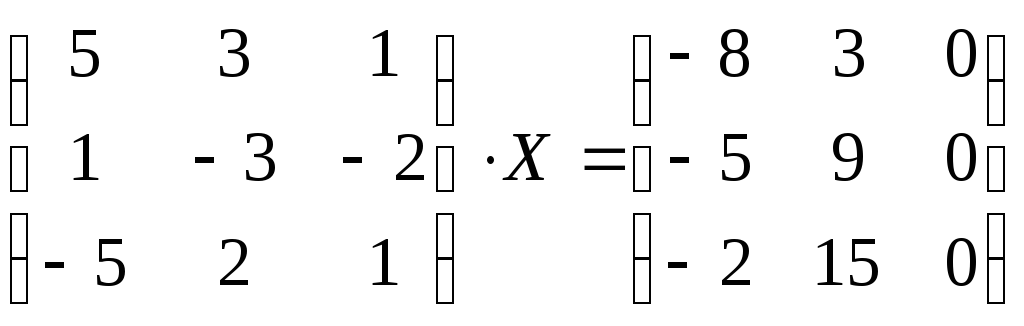 .
.
Вариант 16
-
Вычислить определители:
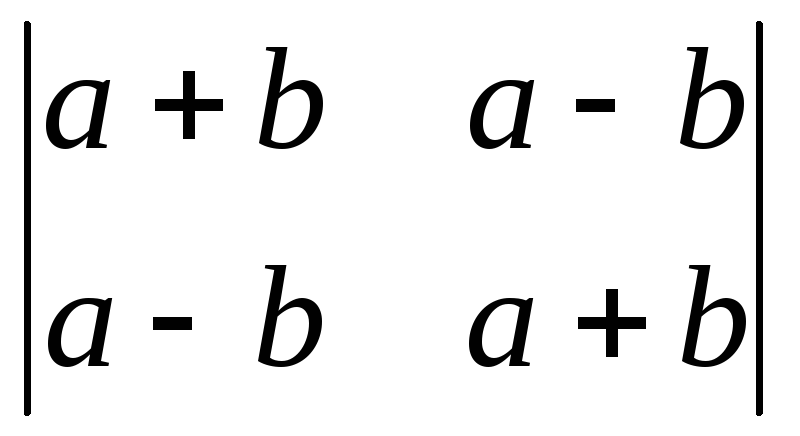 ;
;
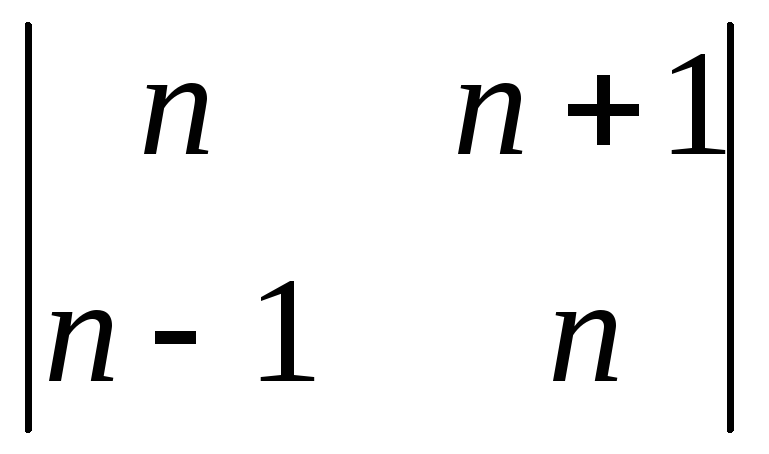 ;
;
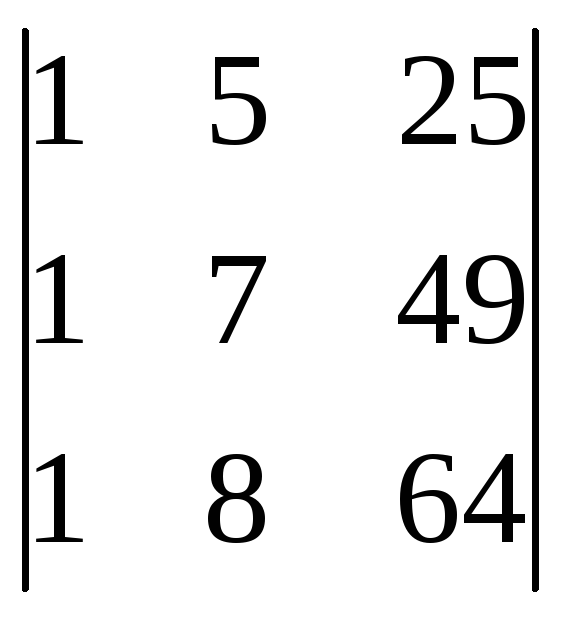 ;
; -
Пользуясь свойствами определителей, вычислить:
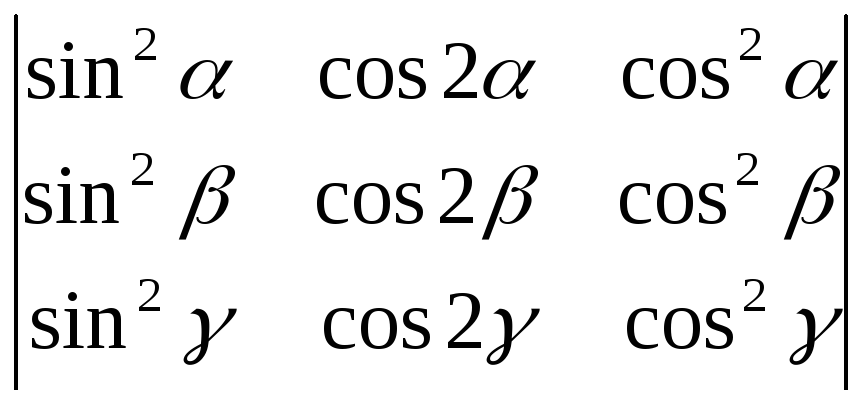 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
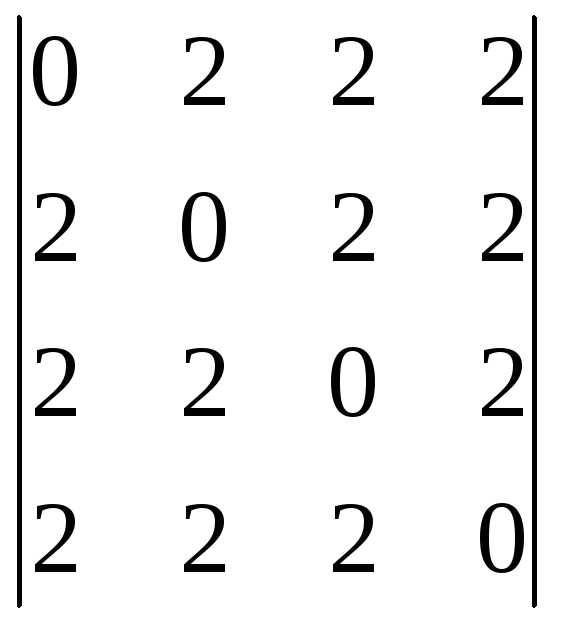 .
.
-
Вычислить произведение матриц:
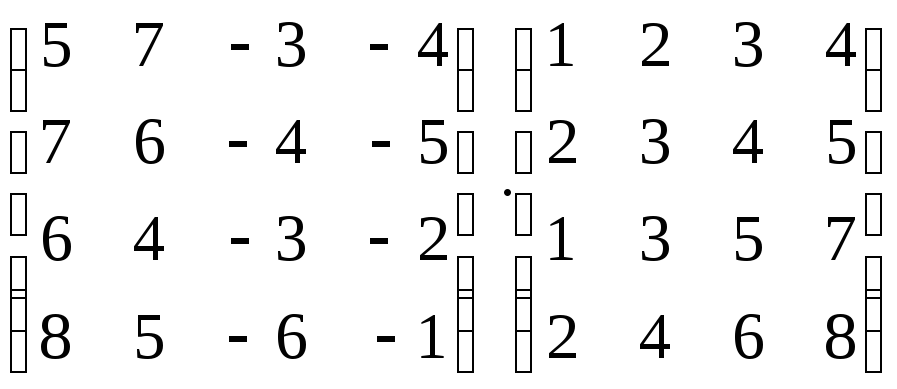
-
Вычислить выражение:
![]()
-
Решить матричные уравнения:
![]() .
.
Вариант 17
-
Вычислить определители:
![]() ;
;
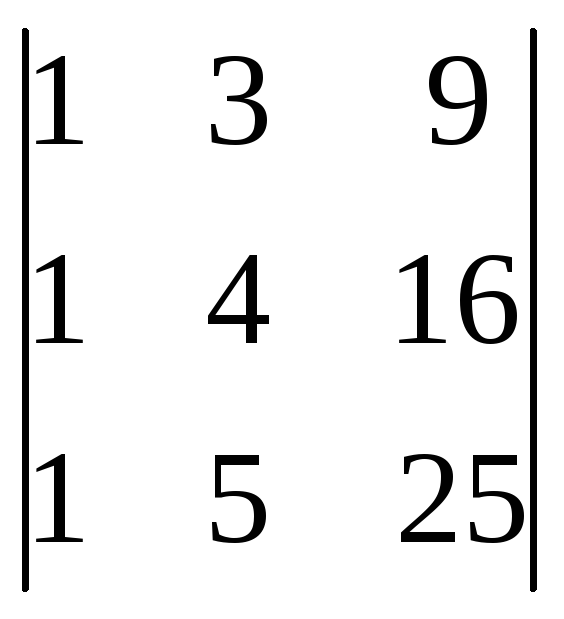 ;
;
-
Пользуясь свойствами определителей, вычислить:
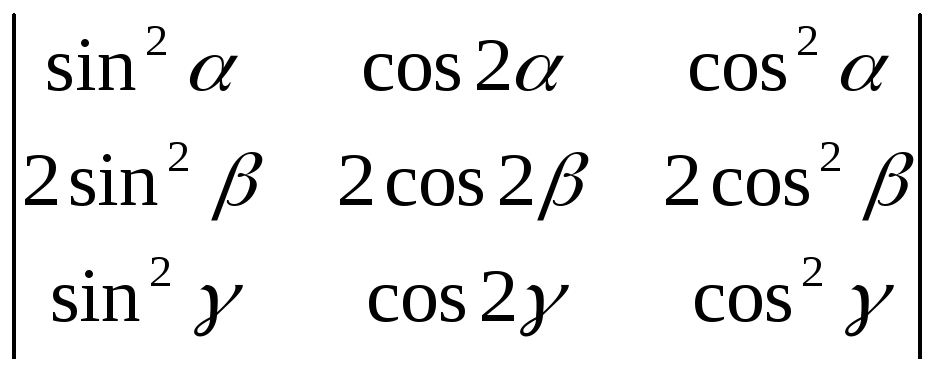 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
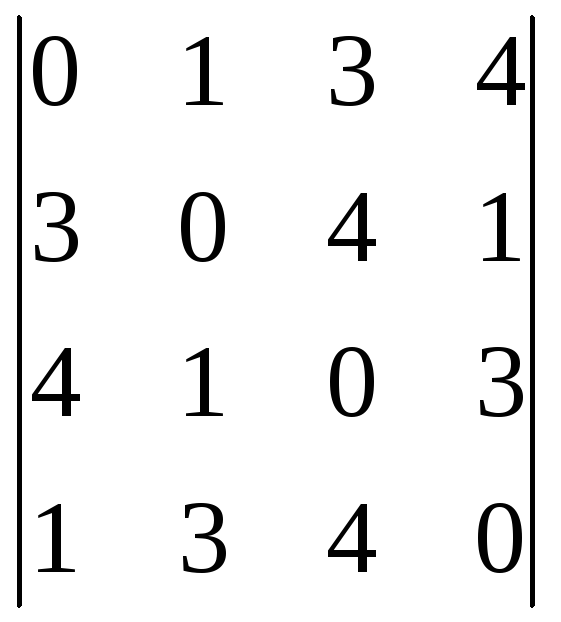 ;
;
-
Вычислить матрицу
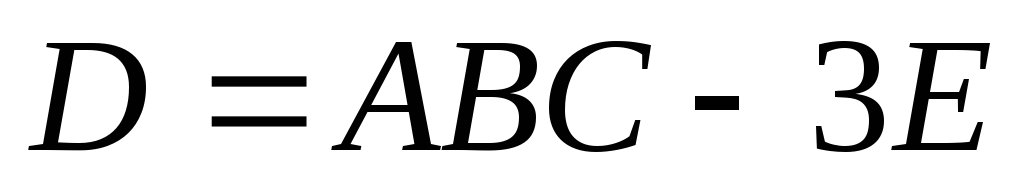 :
:
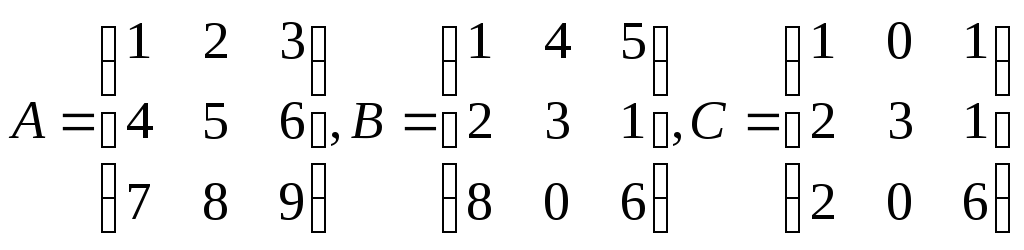 ,
Е –
единичная матрица;
,
Е –
единичная матрица;
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
![]() .
.
Вариант 18
-
Вычислить определители:
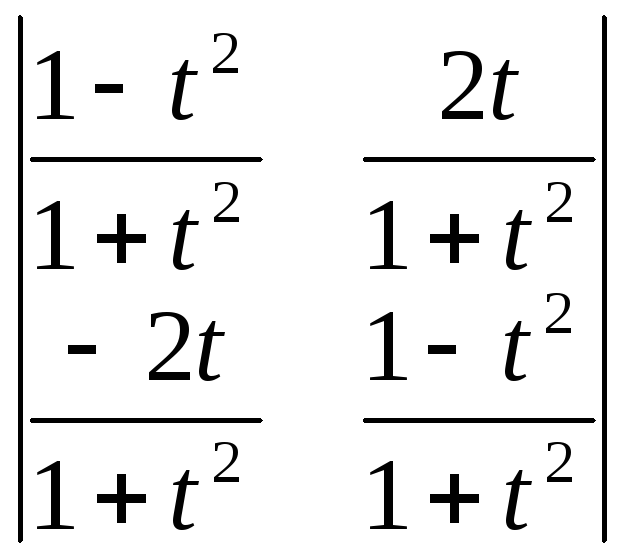 ;
;
 ;.
;. -
Пользуясь свойствами определителей, доказать:
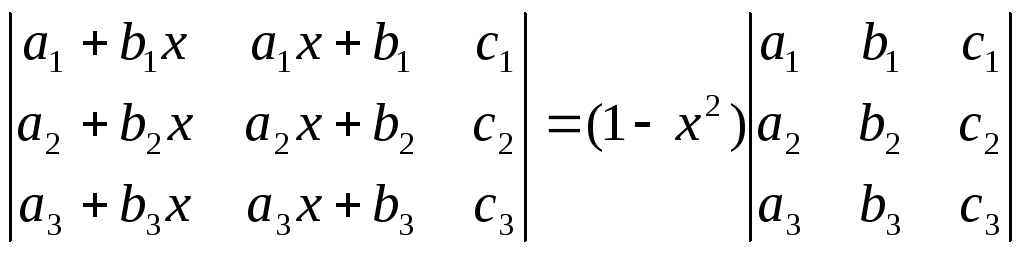 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
 ;
;
-
Найти обратную матрицу для матрицы А:
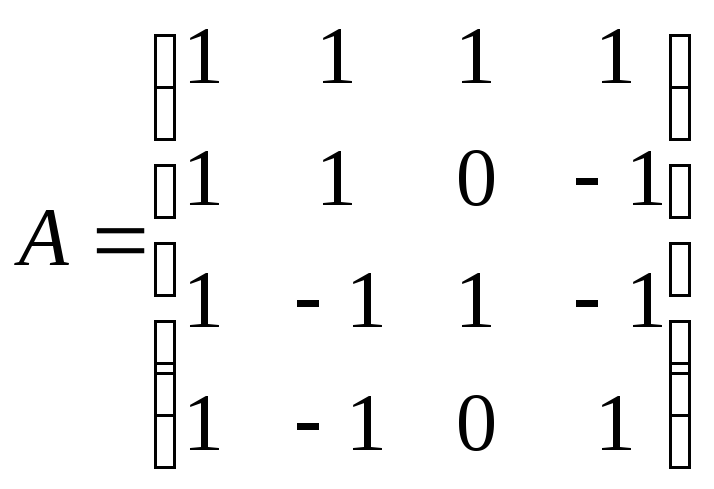 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
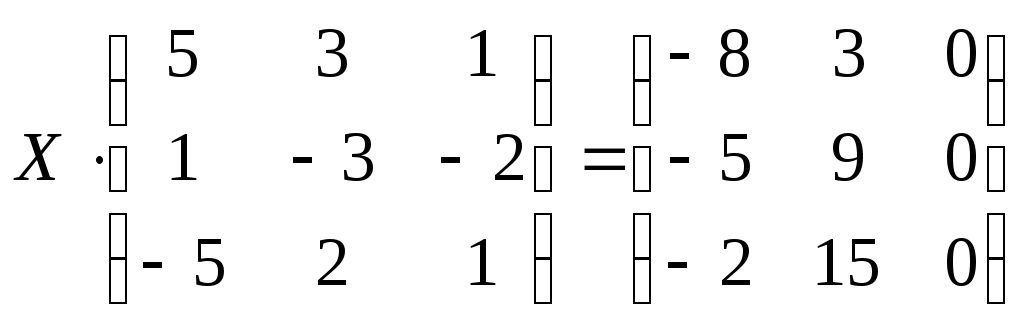 .
.
Вариант 19
-
Вычислить определители:
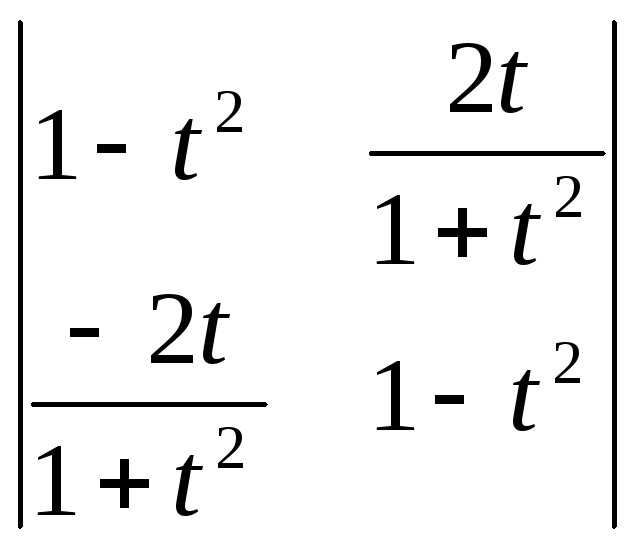 ;
;
 ;
; -
Пользуясь свойствами определителей, вычислить:
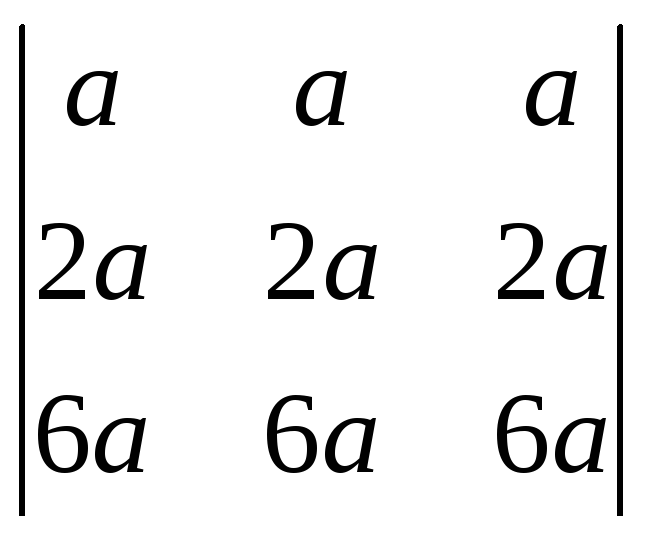 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
 ;
;
-
Найти произведение матриц ABC:
![]() ,
,
![]() ,
,
![]() ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
![]() .
.
Вариант 20
-
Вычислить определители:
![]() ;
;
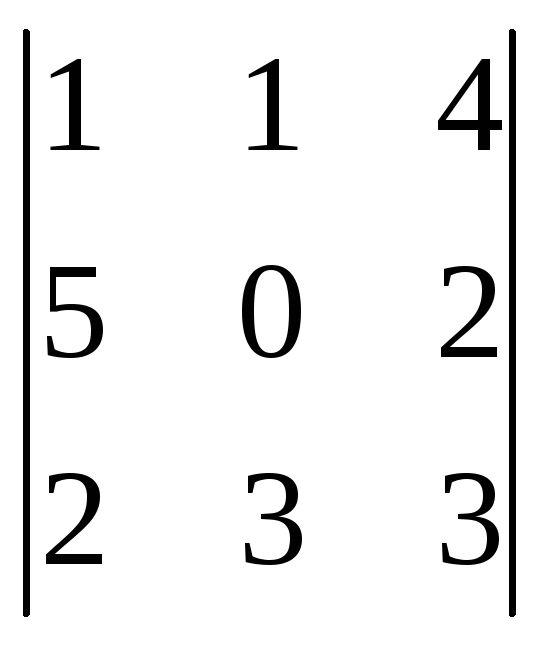 ;
;
 ;
;
-
Пользуясь свойствами определителей, вычислить:
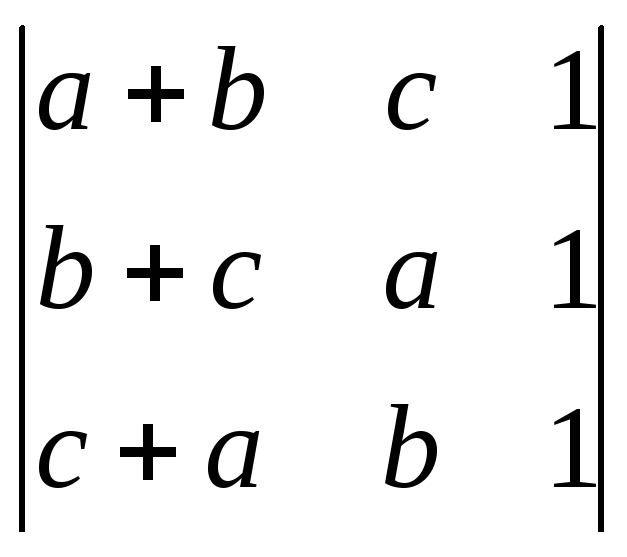 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
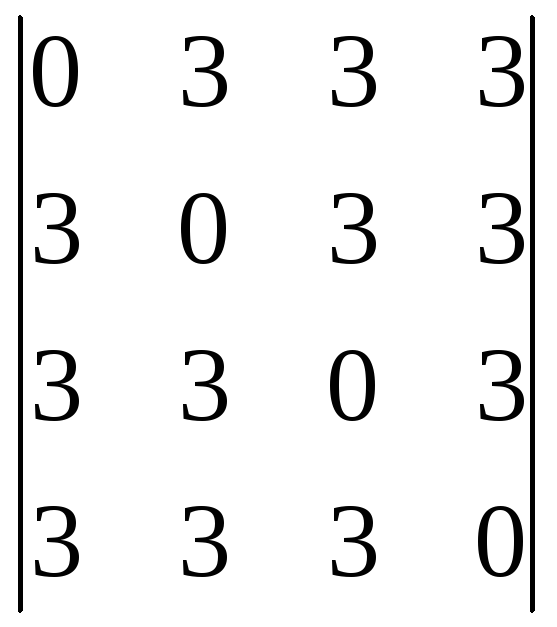 ;
;
-
Вычислить произведение матриц:
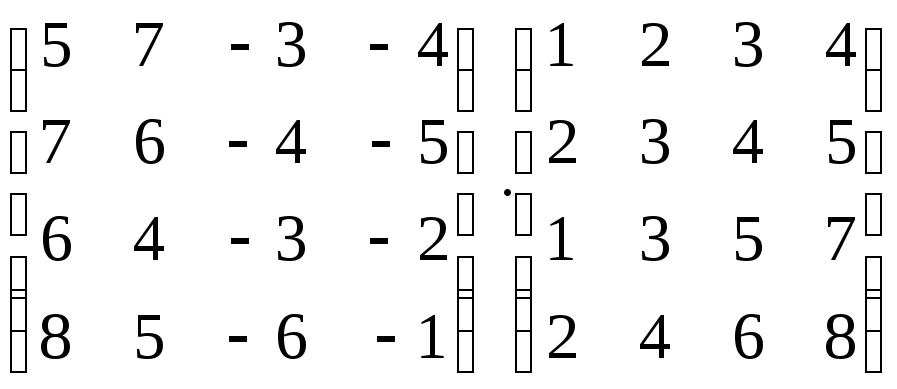 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
![]() ;
;
Вариант 21
-
Вычислить определители:
![]() ;
;
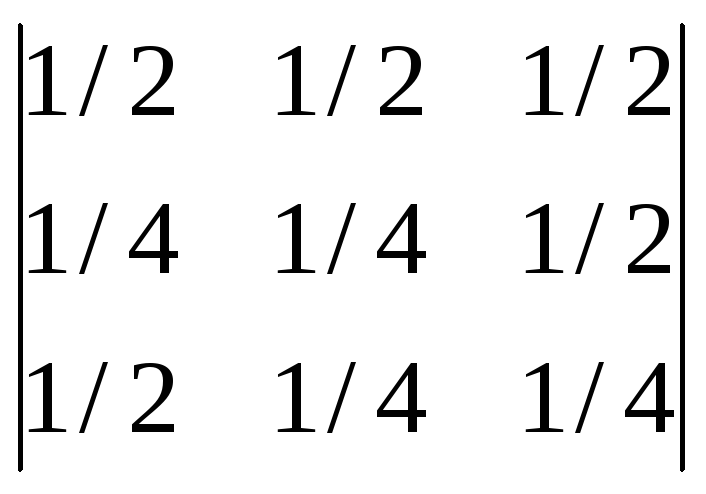 .
.
-
Пользуясь свойствами определителей, вычислить:
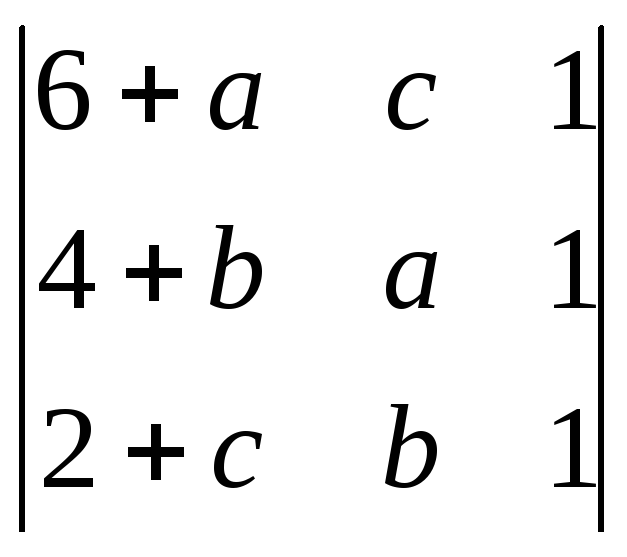 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
 ;
;
-
Вычислить произведение матриц:
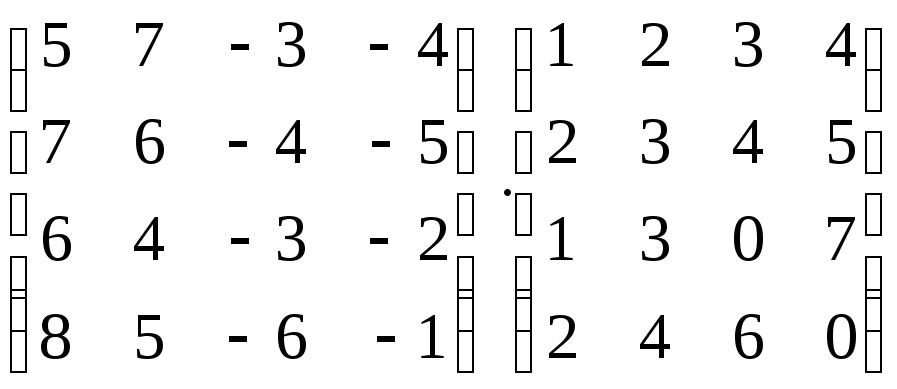 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
![]() .
.
Вариант 22
-
Вычислить определители:
![]() ;
;
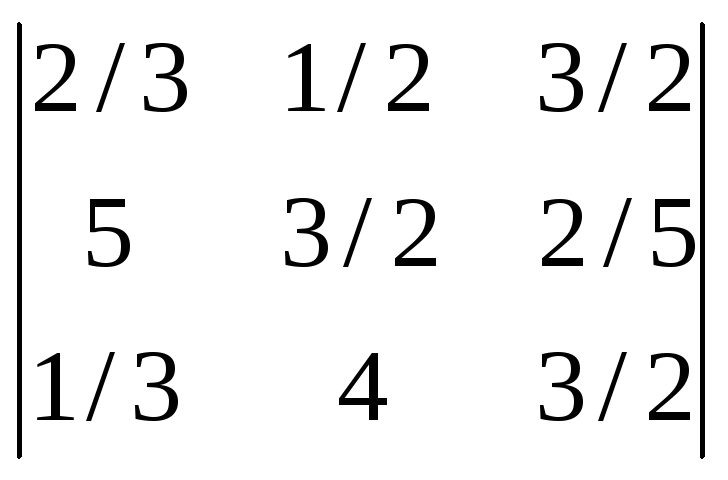
-
Пользуясь свойствами определителей, вычислить:
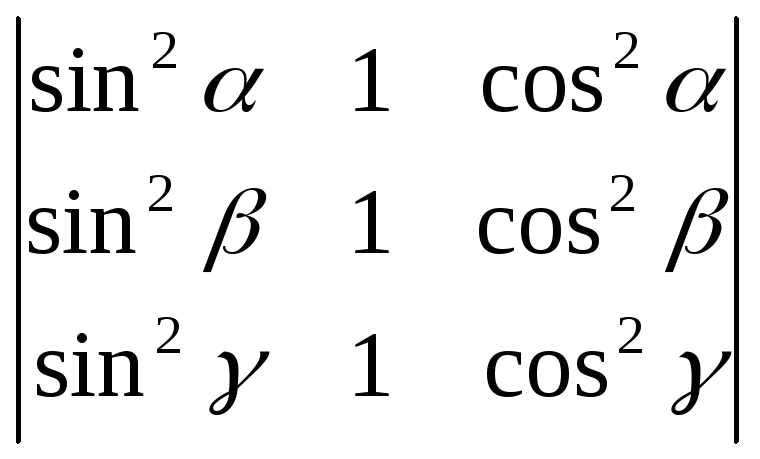 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
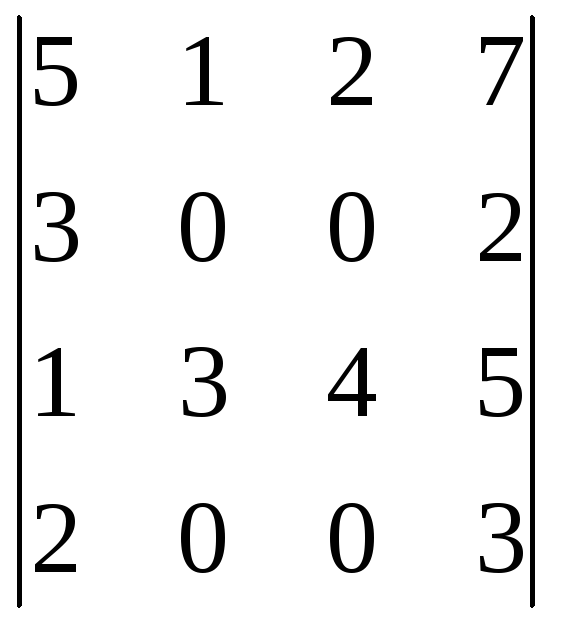 ;
;
-
Вычислить произведение матриц:
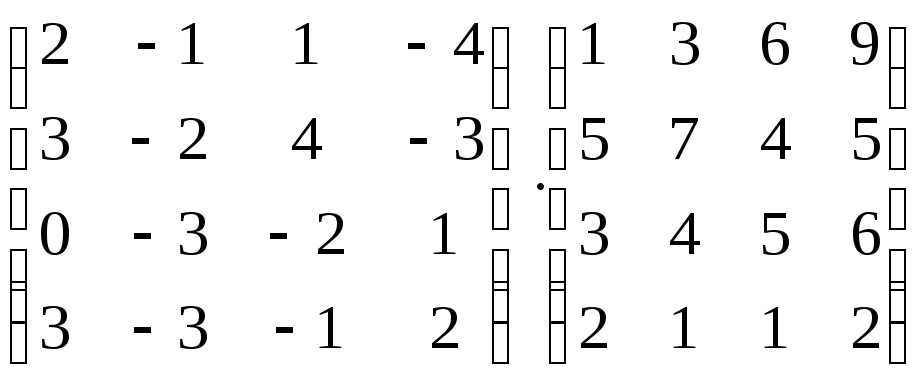 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричные уравнения:
![]() .
.
.
Вариант 23
-
Вычислить определители:
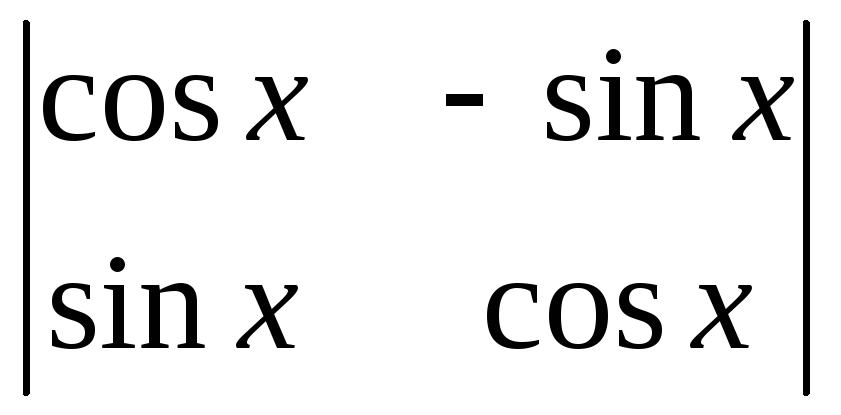 ;
;
 ;
; -
Пользуясь свойствами определителей, доказать:
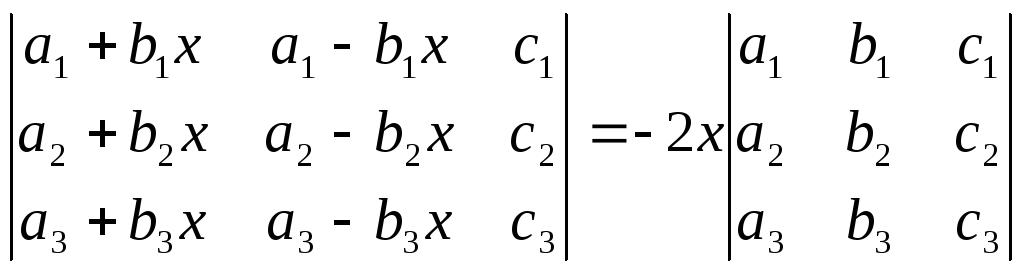 ;
;
-
Пользуясь теоремой Лапласа, вычислить определители:
 ;
;
-
Вычислить произведение матриц:
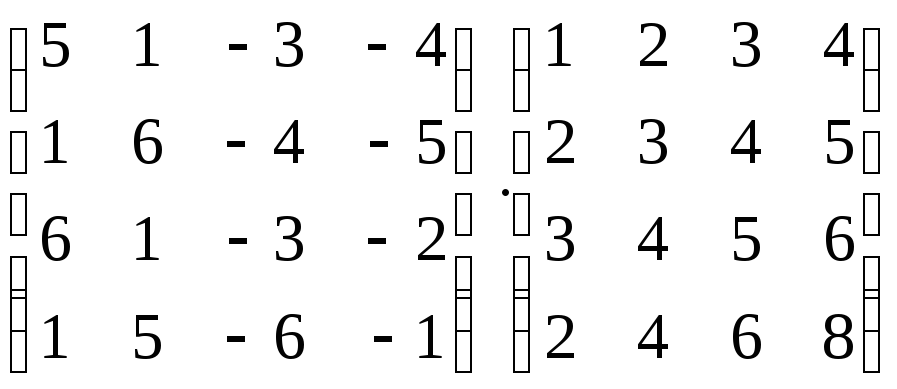 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
![]() .
.
Вариант 24
-
Вычислить определители:
![]() ;
;
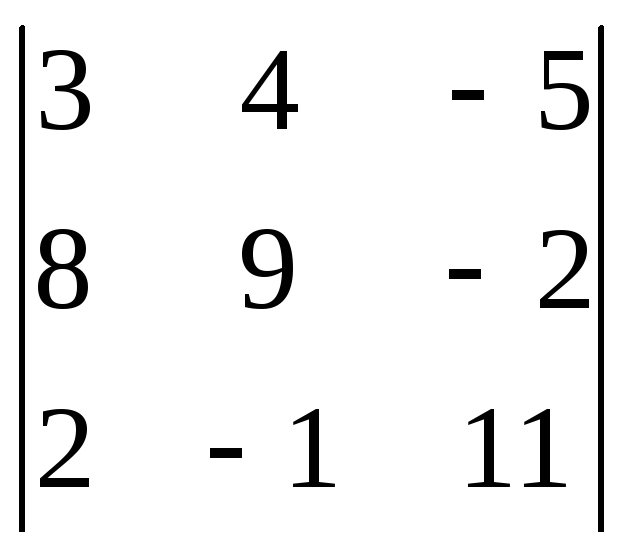 ;
;
-
Пользуясь свойствами определителей, доказать:
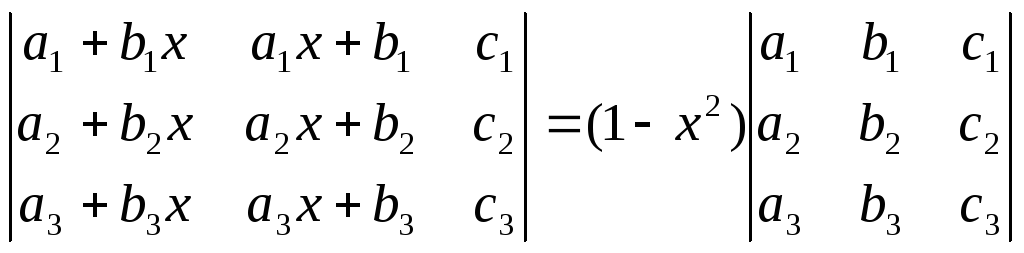 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
 ;
;
-
Найти обратную матрицу для матрицы А:
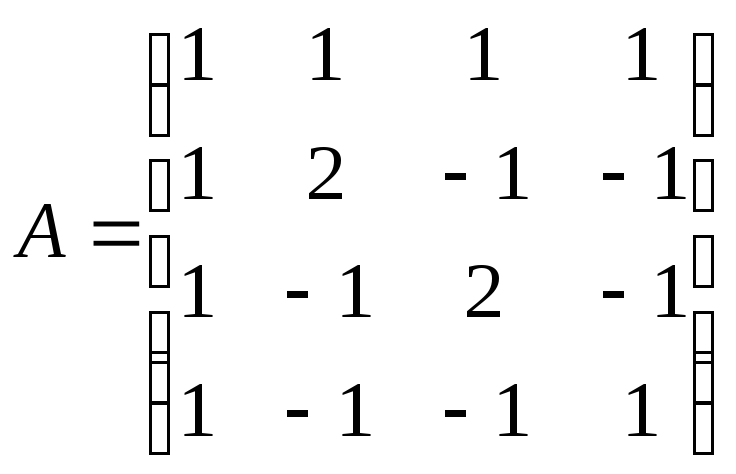 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричное уравнение:
![]() .
.
Вариант 25
-
Вычислить определители:
![]() ;
;
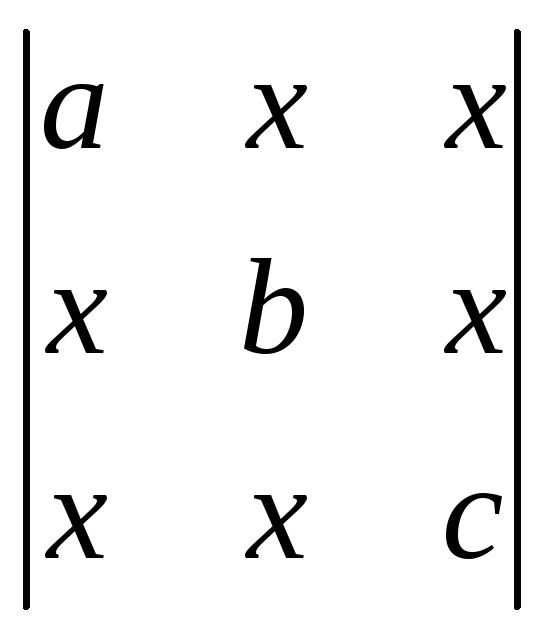 ;
;
-
Верно ли равенство:
 ;
;
-
Вычислить определитель, разложив его по второму столбцу:
 .
.
-
Вычислить выражение:
![]()
-
Найти матрицу D=AT+3AB , где
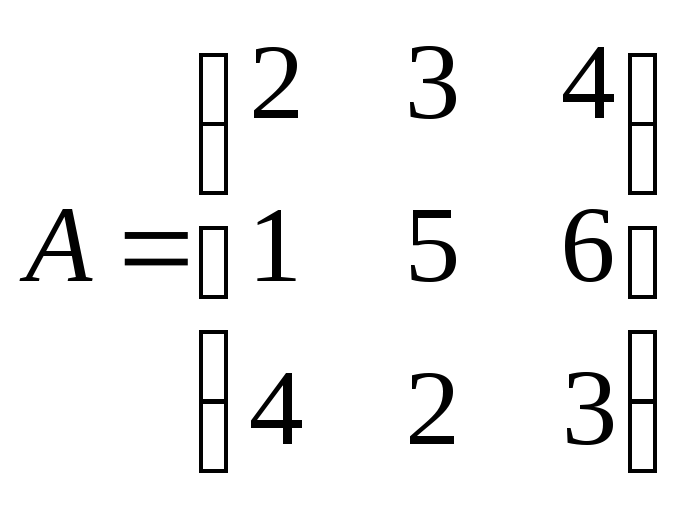 ,
,
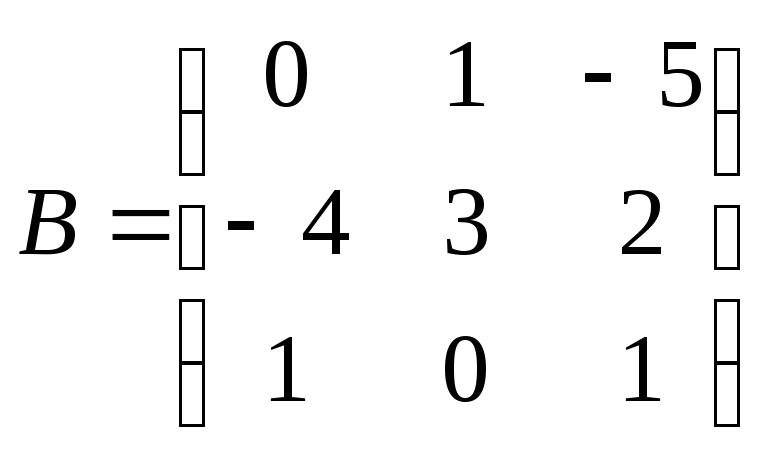 ,
,
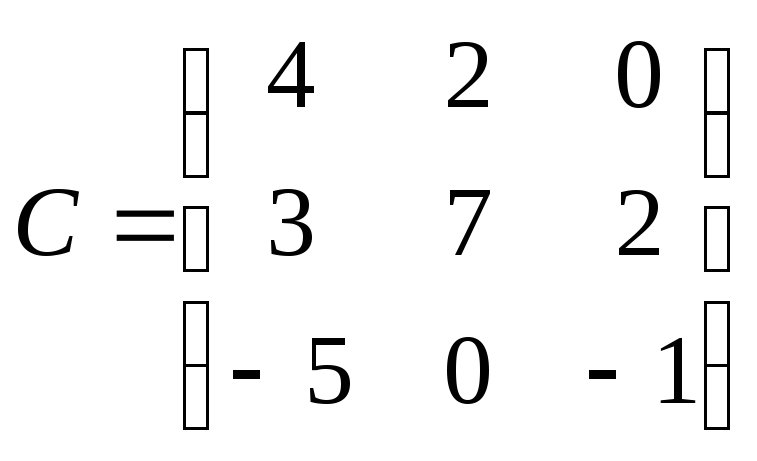 .
.
-
Решить матричное уравнение:
![]() .
.
Вариант 26
-
Вычислить определители:
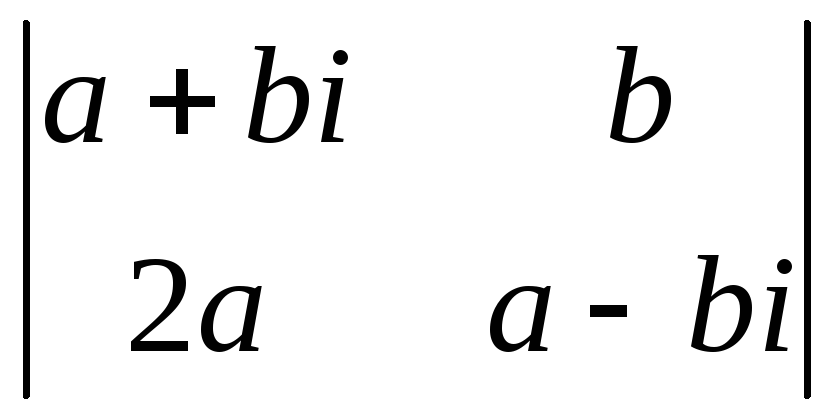 ,
где
,
где
 ;
;
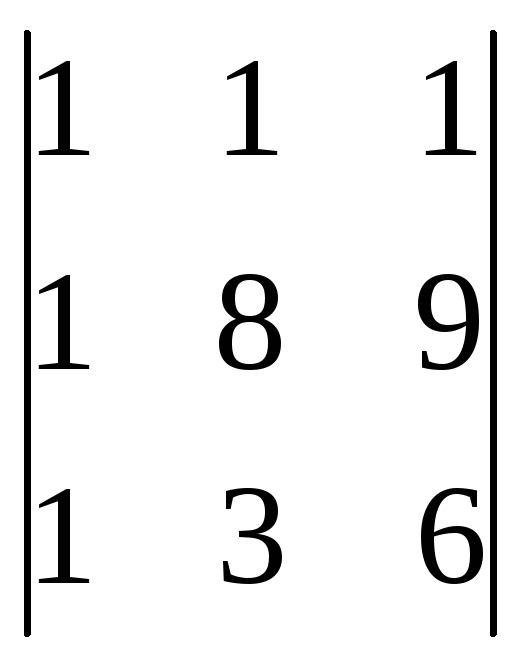 ;
; -
Верно ли равенство:
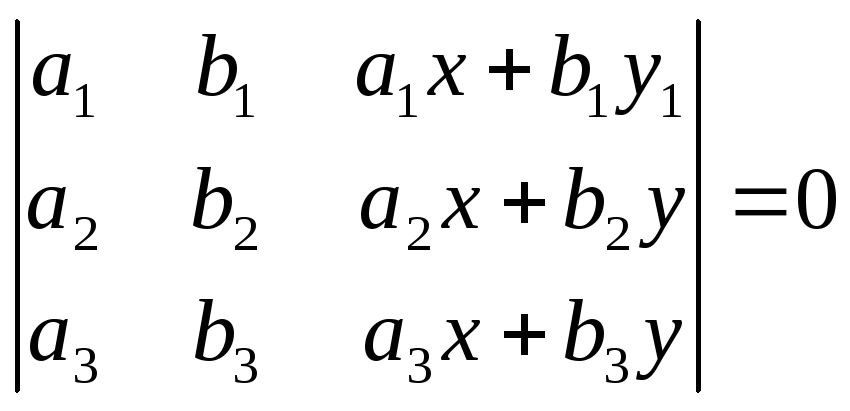 ;
;
-
Вычислить определитель, разложив его по третьему столбцу:
-
 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричные уравнения:
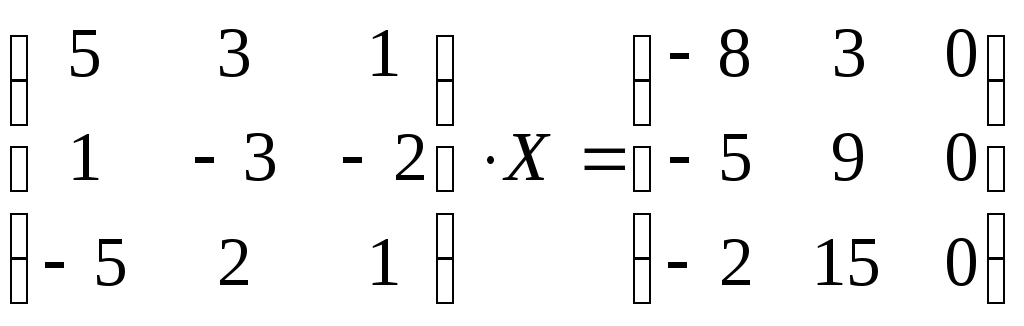 .
.
В-27
1) Вычислить
определители: ![]() ,
где
,
где
![]() ;
;
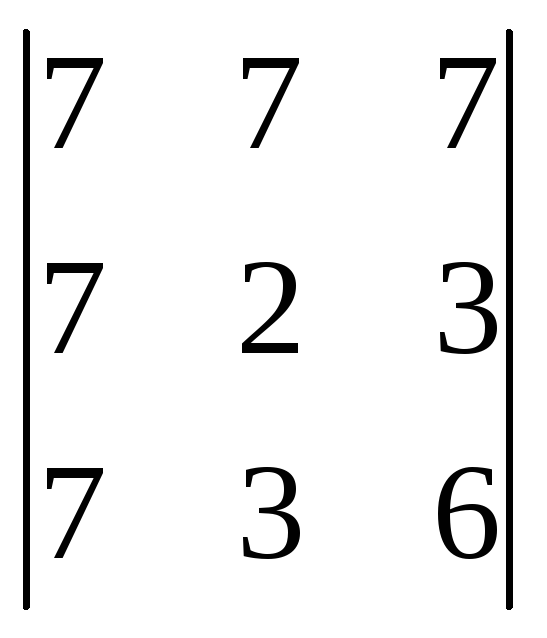 ;.
;.
2)Верно ли равенство:
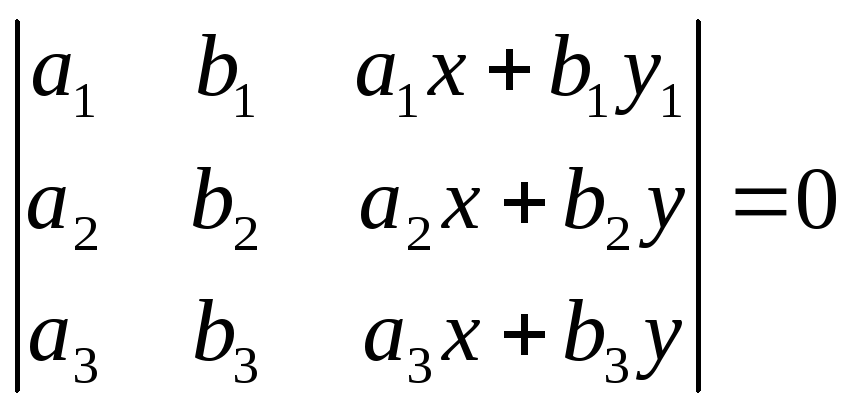 ;
;
3) Вычислить определитель, разложив его по пятому столбцу:
 ;
;
4) Вычислить выражение:
![]() ;
;
5) Решить матричное уравнение:
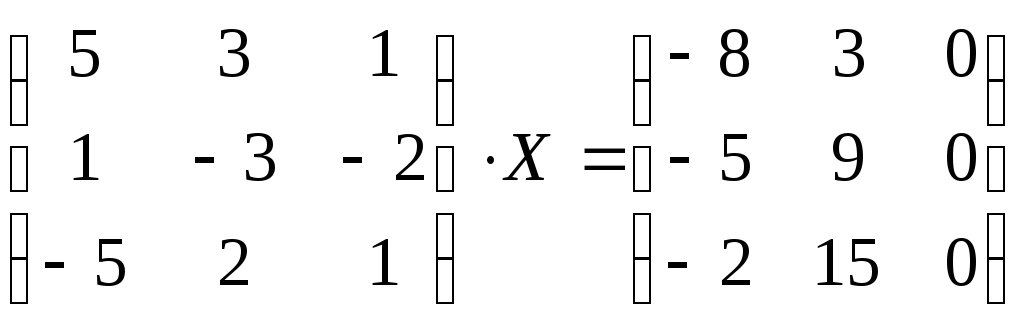 ;
;
6) Вычислить матрицу
![]() ,
если
,
если
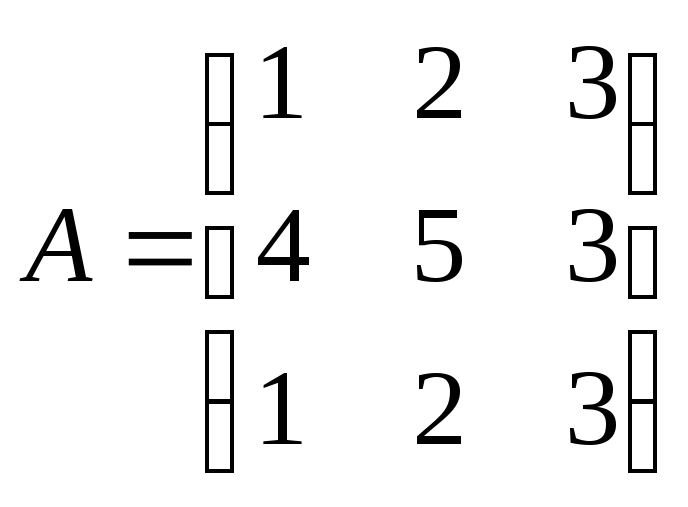 ,
,
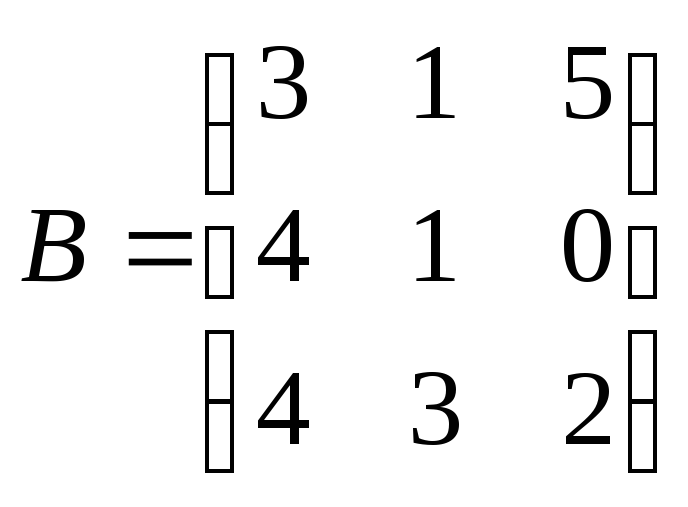 ,
,
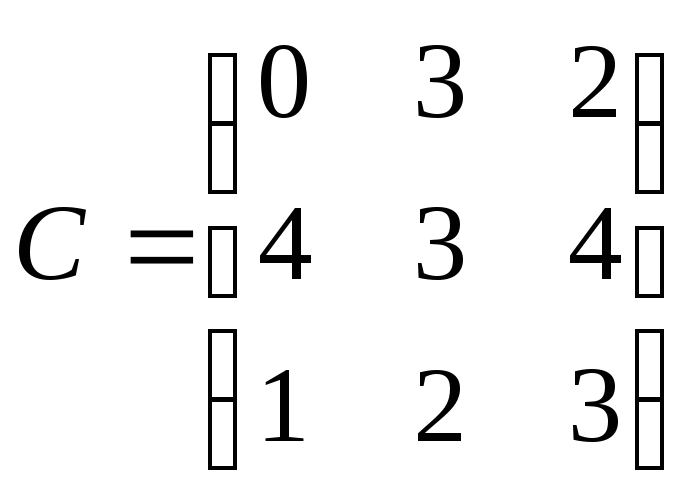 .
.
Вариант 28
-
Вычислить определители:
![]() ;
;
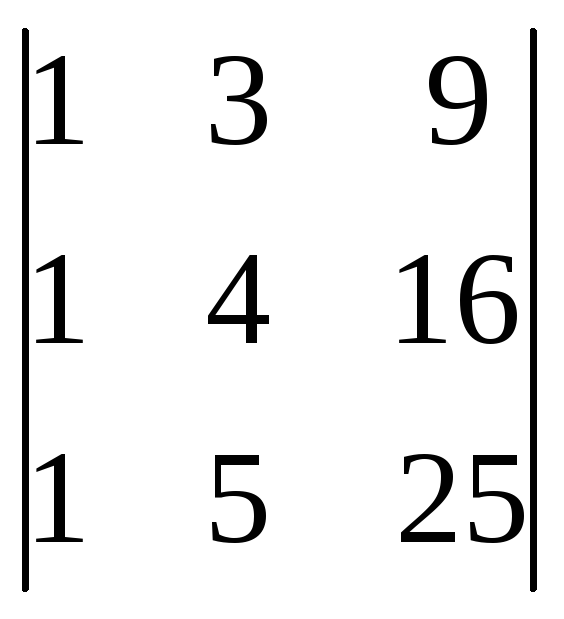 ;
;
-
Пользуясь свойствами определителей, вычислить:
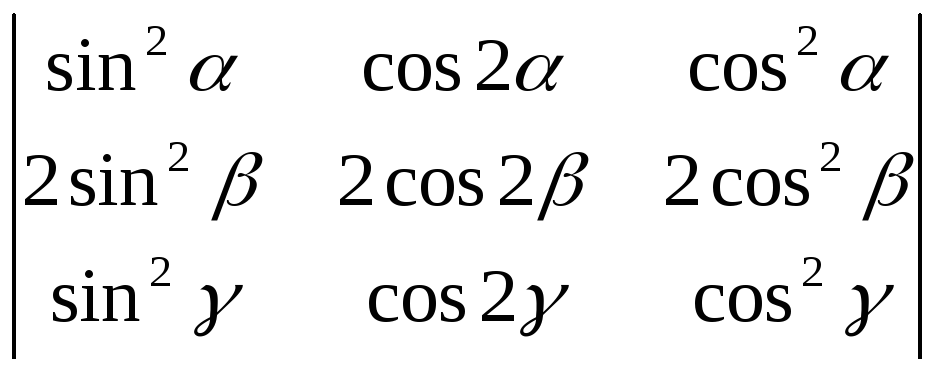 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
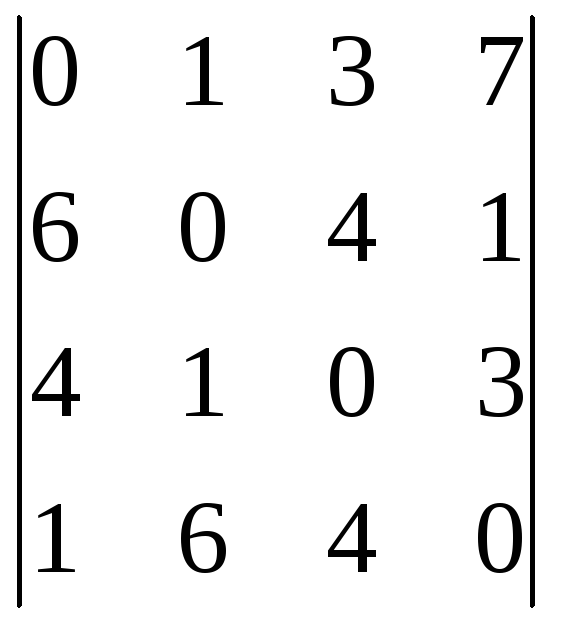 ;
;
-
Вычислить матрицу
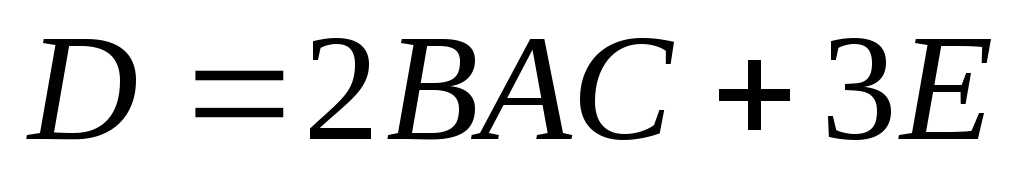 :
:
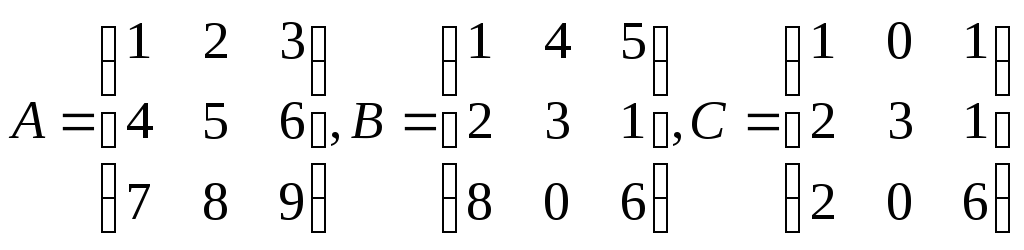 ,
Е –
единичная матрица.
,
Е –
единичная матрица.
-
Вычислить выражение:
![]() ;
;
-
Решить матричные уравнения:
![]() .
.
Вариант 29
-
Вычислить определители:
![]() ;
;
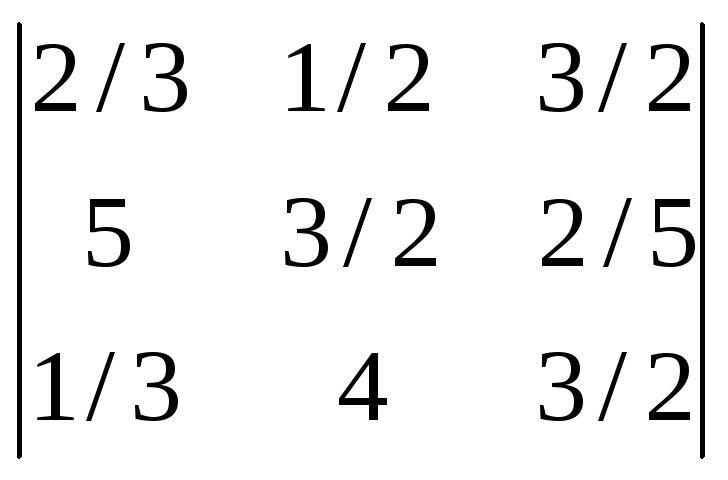
-
Пользуясь свойствами определителей, вычислить:
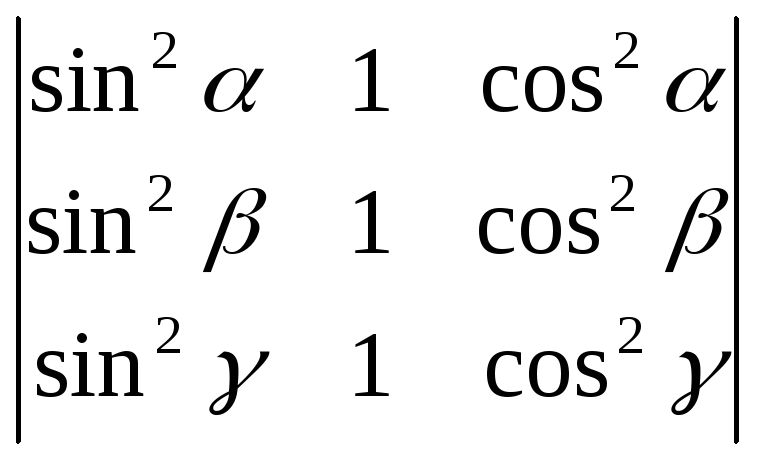 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
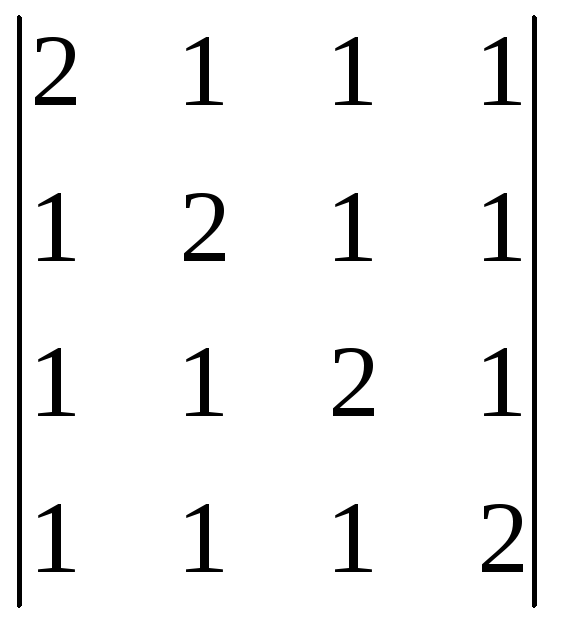 ;
;
-
Вычислить произведение матриц:
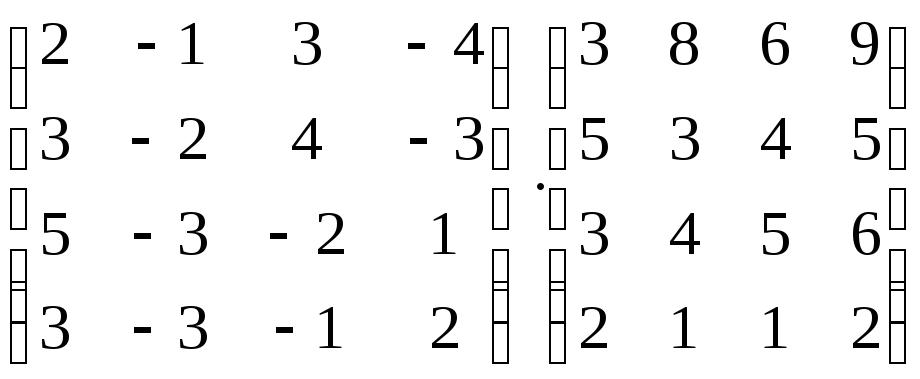 ;
;
-
Решить матричные уравнения:
![]() ;
;
-
Как изменится произведение АВ матриц
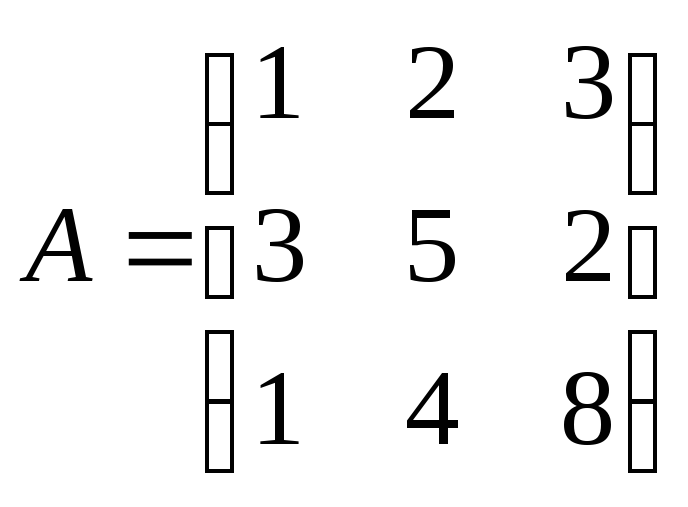 и
и
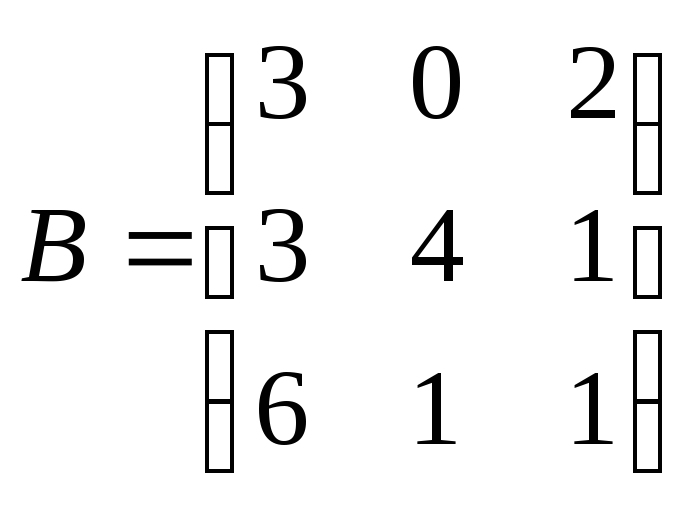 ,
если переставить местами 1-ую и 2-ую
строки матрицы А
?
,
если переставить местами 1-ую и 2-ую
строки матрицы А
?
Вариант 30
-
Вычислить определители:
![]() ;
;
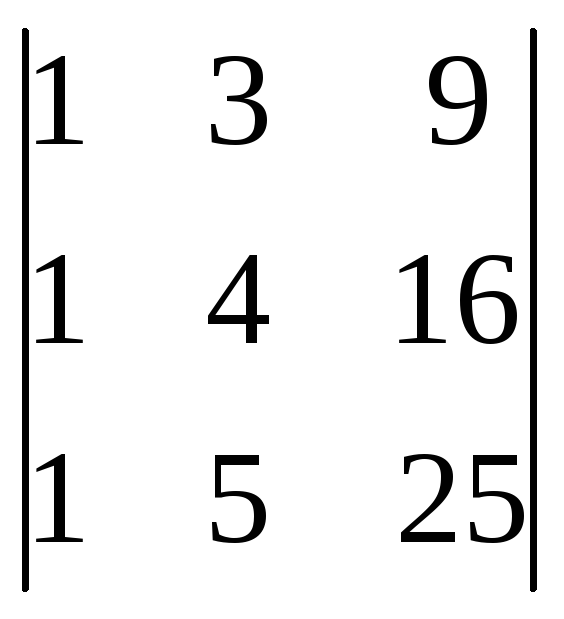
-
Пользуясь свойствами определителей, доказать:
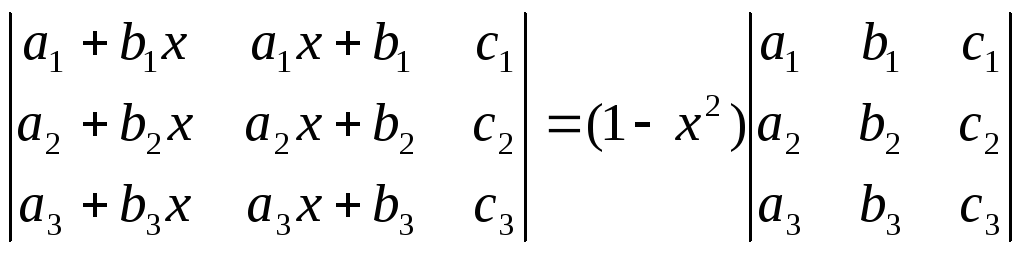 ;
;
-
Пользуясь теоремой Лапласа, вычислить определитель:
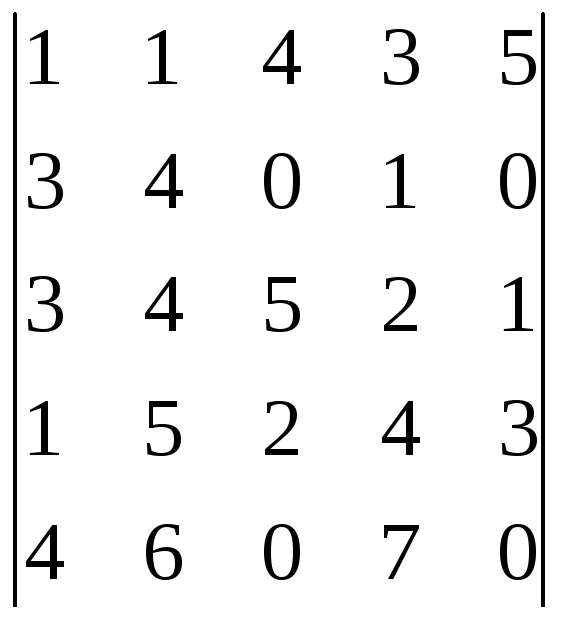 ;
;
-
Найти обратную матрицу для матрицы А:
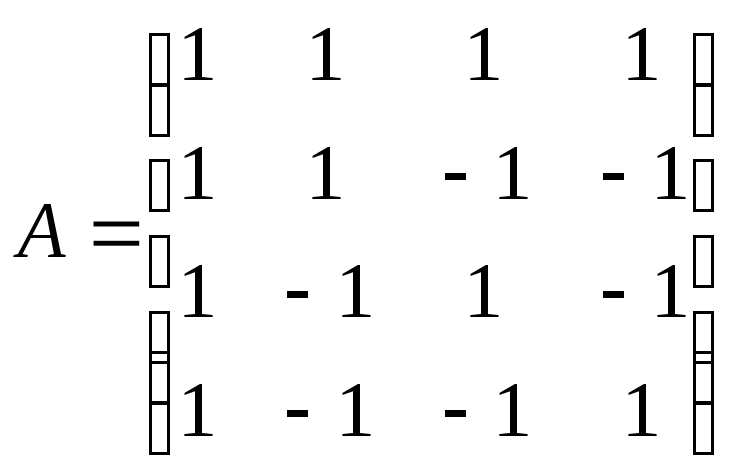 ;
;
-
Вычислить выражение:
![]() ;
;
-
Решить матричные уравнения:
![]() .
.
ЗАДАНИЕ №2
I. Найти решение системы линейных уравнений методом Гаусса.
1) 5х1+3х2+5х3+12х4=10 2) -15х1+2х2 -11х3 -3х4=1
2х1+2х2+3х3+5х4=4 10х1+6х2+7х3 -9х4=3
х1+7х2+9х3+4х4=2 3х1+4х2+2х3 -6х4=2
3) -9х1+6х2+7х3+10х4=3 4) 4х1+7х2+9х3+х4=2
-6х1+4х2+2х3+3х4=2 12х1+3х2+5х3+5х4=10
-3х1+2х2 -11х3 -125х4=1 5х1+2х2+3х3+2х4=4
5) -9х1+10х2+3х3+7х4=7 6) 5х1+6х2+2х3+8х4=7
-4х1+7х2+х3+3х4=5 10х1+9х2+3х3+12х4=13
7х1+5х2 -4х3 -6х4=3 2х1+3х2+х3+4х4=3
7) 12х1+9х2+3х3+10х4=13 8) х1+7х2+3х3 -4х4=5
4х1+3х2+х3+2х4=3 3х1+10х2+7х3 -9х4=7
8х16+6х2+2х3+5х4=7 -4х1+5х2 -6х3+7х4=3
9) -6х1+9х2+3х3+2х4=4 10) 9х1+4х2+х3+7х4=2
-2х1+3х2+5х3+4х4=2 5х1+12х2+5х3+3х4=10
-4х1+6х2+4х3+3х4=3 3х1+5х1+2х3+2х4=4
11) х1 -2х2+х3+х4=1 12) х1+х2 -3х3= -1
х1 -2х2+х3 -х4= -1 2х1+х2 -2х3=1
х1 -2х2+х3+5х4=25 х1+х2 + х3=3
х1+2х2 +3х3=1
13) 2х1 -х2+3х3=3 14) 2х1+х1 -х3+х4=1
3х1+х2 -5х3=0 3х1 -2х2+2х3 -3х4=2
4х1 -х2+х3=3 5х1+х2 -х3+2х4= -1
х1+3х2 -13х3= -6 2х1 -х2+х3 -3х4=4
15) х1 -2х2+3х3 - 4х4=4 16) 2х1+х2 -х3 -х4+х5=1
х2 - х3+х4 = -3 х1 -х2+х3+х4 -2х5=0
х1+3х2 -3х4=1 3х1+3х2 -3х3 -3х4+4х5=2
х1 -7х2+3х3+х4= -3 4х1+5х2 -5х3 -5х4+7х5=3
17) 3х1+х2 -2х3+х4 -х5=1 18) х1+3х2+5х3 -4х4=1
2х1 -х2+7х3 -3х4+5х5=2 х1+3х2+2х3 -2х4= -1
х1+3х2 -2х3+5х4 -7х5=3 х1 -2х2+х3 -х4=3
3х1 -2х2+7х3 -5х4+8х5=3
19) х1 -2х2+3х3 -4х4+2х5= -2 20) х1+2х2+3х3 -х4=1
х1+2х2 -х3 -х5= -3 3х1+2х2+х3 -х4=1
х1 -х2+2х3 -3х4 =10 2х1+3х2+х3+х4=1
х1 -х3+х4 -2х5= -5
21) 2х1+7х2+3х3+х4=6 22) 2х1 -3х2+5х3+7х4=1
3х1+5х2+2х3+2х4=4 4х1 -6х2+2х3+3х4=2
9х1+4х2+х3+7х4=2 2х1 -3х2 -11х3 -15х4=1
23) 3х1+4х2+х3+2х4=3 24) 3х1 -5х2+2х3+4х4=2
6х1+8х2+2х3+5х4=7 7х1 -4х2+х3+3х4=5
9х1+12х2+3х3+10х4=13 5х1+7х2 -4х3 -6х4=3
25) 2х1+5х2 -8х3=8 26) 3х1 -2х2+5х3+4х4=2
4х1+3х2 -9х3=9 6х1 -4х2+4х3+3х4=3
2х1+3х2 -5х3=7 9х1 -6х2+3х3+2х4=4
х1+8х2 -7х3=12
27) 2х1 -х2+3х3 -7х4=5 28) 9х1 -3х2+5х3+6х4=4
6х1 -3х2+х3 -4х4=7 6х1 -2х2+3х3+х4=5
4х1 -2х2+14х3 -31х4=18 3х1 -х2+3х3+14х4= -8
29) 3х1+2х2+2х3+2х4=2 30) х1+х2+х3 -Х4+3х5=1
2х1+3х2+4х3 -х4+3х5=2 2х1+2х2+4х3 -х4+3х5=2
9х1+х2+4х3 -5х4=1 3х1+3х2+5х3 -2х4+3х5=1
2х1+2х2+3х3+4х4=5 2х1+2х2+8х3 -3х4+9х5=2
II. С помощью правила Крамера и матричным методом решить следующие системы уравнений.
1) 2х1 - х2 - х3= 4 2) х1+х1+2х3=-1
3х1+4х2 - 2х3=11 2х1- х2+2х3=-4
3х1 -2х2+4х3=11 4х1+ х2+4х3=-2
3) 3х1+2х2+х3=5 4) х1+2х2+4х3=31
2х1+3х2+х3=1 5х1+х2+2х3=29
2х1+х2+3х3=11 3х1- х2+ х3 =10
5) 5х1 -6х2+4х3=3 6) 4х1 -3х2+2х3= -4
3х1 -3х2+2х3=2 6х1 -2х2+3х3= -1
4х1 -5х2+2х3=1 5х1 -3х2+2х3= -3
7) 5х1+2х2+3х3= -2 8) 2х1+х2+3х3=1
2х1 -2х2+5х3=0 5х1+3х2+2х3=2
3х1+4х2+2х3= -10 х1+4х2+3х3=3
9) 3х1+2х2+х3=1 10) 4х1 -3х2+5х3=2
2х1+5х2+3х3=2 3х1 -2х2+8х3=3
3х1+4х2+2х3=3 х1 -7х2 -5х3=1
11) х1+ х2 -х3=0 12) 2х1 - х2 - х3=3
х1 - х2 +х3=2 -х1+2х2 - х3=-3
-х1+х2 +х3=4 -х1 - х2 +3х3=2
13) 2х1-3х2+3х3=-2 14) х1+х2+-х3=0
2х1 - х2+ х3= 2 х1 - х2+ х3=4
х1 + х2+ х3=6 -х1+ х2+ х3=2
15) 2х1 - х2 - х3=2 16) 2х1-3х2 +3х3=3
-х1+2х2 -х3=3 2х1 - х2 + х3 =5
-х1 - х2+3х3=2 х1 + х2 + х3=6
17) 2х1 - х2 - 2х3=2 18) х1 +2х2 - х3=1
х1+ х2 +2х3=1 2х1 - х2 - х3 =3
х1 + 2х2+3х3=2 х1 - х2 +3х3=5
19) х1 - х2 - х3=0 20) 2х1- х2 +х3=-2
2х1+х2 +3х3=7 -х1 - 2х2 - х3 =-1
-х1 +2х2 - х3=-5 3х1 +4х2 - х3=5
21) 3х1 + х2 - х3=-4 22) 4х1 - х2 +2х3=3
2х1+2х2 +3х3=6 3х1 - 2х2 - х3 =1
х1 + 3х2 - х3=0 2х1 +3х2 +2х3=11
23) 4х1 + х2 - 2х3=-8 24) -2х1+х2 - х3=0
-3х1 -2х2 +х3=5 х1 - 2х2 + х3 =-5
-2х1 -3х2 - х3=0 -3х1 +3х2 +2х3=1
25) -х1 - х2 - х3=-2 26) х1 +х2 +2х3=2
2х1+2х2 +х3=3 2х1 - х2 - 2 х3 =-5
х1 +2х2+3х3=6 х1 +2х2 +3х3=3
27) х1 +2 х2 - х3=4 28) х1- х2 - х3=0
2х1 - х2 -х3=3 2х1 - х2 - х3 =3
х1 - х2+3х3=1 х1 - х2 +3х3=1
29) х1 - х2 - х3=0 30) 2х1 - х2 +х3=-1
2х1+х2 +3х3=6 -х1 - 2х2 - х3 =6
-х1 + 2х2 - х3=2 3х1 + 4х2 - х3=-10
III. Исследовать системы уравнений и решить, если они совместны.
1) 2х1+7х2+3х3+х4=6 2) 2х1 -3х2+5х3+7х4=1
3х1+5х2+2х3+2х4=4 4х1 -6х2+2х3+3х4=2
9х1+4х2+х3+7х4=2 3х1 -3х2 -11х3 -15х4=1
3) 3х1+4х2+х3+2х4=3 4) 3х1 -2х2+5х3+х4=2
6х1+8х2+2х3+5х4=7 6х1 -4х2+4х3+3х4=3
9х2+12х2+3х3+10х4=13 9х1 -6х2+3х3+2х4=4
5) 2х1 -х2+3х3 -7х4=5 6) 9х1 -3х2+5х3+6х4=4
6х1 -3х2+х3 -4х4=7 6х1 -2х2+3х3+х4=5
4х1 -2х2+14х3 -31х4=18 3х1 -х2+3х3+14х4= -8
7) 3х1+2х2+2х3+2х4=2 8) 2х1 -х2+х3+2х4=2
2х1+3х2+2х3+5х4=3 6х1 -3х2+2х3+4х4=3
9х1+х2+4х3 -5х4=1 6х1 -3х2+4х3+8х4=9
2х1+2х2+3х3+4х4=5
7х1+х2+6х3 -х4=7
9) 4х1+5х2+2х3+3х4=1 10) х1+2х2+3х3 -2х4=4
2х1+4х2+х3+2х4=3 3х1+6х2+5х3 -4х4=5
2х1 -2х2+х3 = -7 х1+2х2+7х3 -4х4=11
11) 6х1+3х2+2х3+3х4=5 12) х1+9х2+4х3 -5х4=1
4х1+2х2+х3+2х4=4 3х1+2х2+2х3+5х4=3
4х1+2х2+3х3+2х4=0 2х1+3х2+2х3+2х4=2
х1+7х2+6х3 -х4=7
2х1+2х2+3х3+4х4=5
13) 3х1 -6х2 -х3+4х4= -7 14) 2х1+х2+3х3 -2х4=4
х1 -2х2 -3х3+7х4= -5 6х1+3х2+5х3 -4х4=5
2х1 -4х2 -14х3+31х4= -10 2х1+х2+7х3 -4х4=11
15) х1 -2х2 +2х3 - 4х4= 1 16) 4х1+3х2-3х3 -х4=4
х1 - х2 + х3 - х4= 0 3х1 -х2+3х3 -2х4=1
х1 - х2 - 5х3 - х4= 4 3х1 +х2 - х4 = 0
х1 - х2 + 6х3 - х4= 5 5х1+4х2 - 2х3 +х4=3
17) 2х1 -4х2 +3х3 - 2х4= 3 18) 2х1-3х2-х3 +2х4=3
х1 -2х2 -2х3 - х4= -2 3х1+5х2+9х3 -4х4=-8
3х1 -6х2 +5х3-3х4= 5 4х1-3х2+5х3 +7х4=14
4х1 -8х2 -3х3-4х4=-3
19) 2х1 -х2 +3х3-2х4= 4 20) 2х1 + х3 + 3х4 =-1
4х1 -2х2 +5х3+х4=7 -2х2+5х3 +5х4=-3
2х1 -х2 + х3+8х4= 2 х1+ х2 - х4 =1
2х1 - х2 +2х3+3х4=3 х1 -3х2+2х3 +9х4=-5
21) 2х1 +х2 = 1 22) 2х1+х2+х3 +х4=7
3х1 +х2 = 2 х1 - х3 - х4=2
х1 + х2 +3х3+4х4=0 х1+х2 - х4 =3
2х1 - х2 +2х3 +3х4=0 х1+х2+ х3 =4
23) 2х1 +х2 - 5х3+х4=8 24) 3х1 - 2х1 +5х3 +4х4 =2
х1 -3х2 - 6х4=9 6х1 - 4х2+4х3 +3х4=3
2х2 - х3+2х4= -5 9х1 - 6х2 + 3x3+2х4 =4
х1 +4х2 -7х3+6х4=0 15х1 -10х2+7х3 +5х4=7
25) 2х1 +х2 - 4х3+х4=0 26) 2х1 - 4х2 +3х3 +х4 =0
х1 +2х2 -x3 - 6х4=0 х1 - 2х2 + х3 - 4х4=2
7x1+4х2 +6х3 -5х4=0 х2 - x3+3х4 =1
х1 + 8х3+7х4=1 4х1 -7х2+4х3 - 4х4=5
27) х1 +2х2 +3х3+4х4=1 28) х1 - 2х1 -3х3 -х4 =-2
2х1+3х2 +х3 + х4=2 х1 + 3х2 - 5х3 +2х4=-2
х1+ х2 + х3 - х4= 0 -х1 + 4х2 + x3 - 3х4 =6
х1 - 2х3 - 6х4=-1 3х1 + х2 -13х3 +х4=-7
29) -2х1 +х2 - х3+5х4=- 4 30) х1 + х1 + х3 =3
2х1+3х2 -3х3 + х4=2 х1 + х2 - 3х3=-1
8х1 - х2 + х3 - х4= 1 2х1 + х2 - 2x3 = 1
4х1 -3х2 +3х3+3х4=2 х1 +2х2 -3х3 =7
IV. Найти общее решение и фундаментальную систему решений для систем однородных уравнений.
1) -2х1+3х2+4х3+5х4=0 2) 11х1+4х2 -8х3+17х4=0
6х1 -4х2+3х3+5х4=0 2х1+3х2 -6х3+4х4=0
24х1 -19х2+3х3+3х4=0 3х1+2х2 -4х3+5х4=0
4х1 -3х2+х3+2х4=0
3) 2х1+4х2+3х3+8х4=0 4) 9х1+9х2 -3х3+4х4=0
6х1+7х2+9х3+9х4=0 7х1+6х2 -2х3+2х4=0
4х1+5х2+7х3+6х4=0 х1+6х2 -2х3+6х4=0
5) х1 -х2+х5=0 6) 5х1+6х2 -2х3+7х4+4х5=0
х2 -х4+х6=0 2х1+3х2 -х3+4х4+2х5=0
х1 -х2+х5 -х6=0 7х1+9х2 -3х3+5х4+6х5=0
х2 -х3+х6=0 5х1+9х2 -3х3+х4+6х5=0
х1 -х4+х5=0
7) 3х1+4х2+х3+2х4=0 8) 2х1 -х2+5х3+7х4=0
5х1+7х2+х3+3х4=0 4х1 -2х2+7х3+5х4=0
4х1+5х2+2х3+х4=0 2х1 -х2+х3 -5х4=0
9) 20х1+3х2+6х3 -2х4=0 10) 7х1+5х2+6х3+3х4=0
6х1+3х2+3х3 -х4=0 -3х1 -5х2 -14х3+х4=0
4х1+9х2+6х3 -2х4=0 8х1+5х2+4х3+4х4=0
11) х2+х3+ х4=0 12) 3х1 +х2+х3+4х4=0
х1 - х3 - х4=0 4х2+10х3+х4=0
х1+ х2 -х4=0 х1 +7х2+17х3 +3х4=0
х1+ х2+х3 =0 2х1 +2х2+4х3 3х4=0
13) 2х1 -3х2 +3х3+3х4=0 14) -х1 +х2 -2х3 -3х4 =0
х1+2х2 - 4х3 - 9х4=0 х1 - 2х2+3х3 +5х4=0
- х1+3х2 - х3 +4х4=0 -2х1 +4х2 - 3x3 - х4 =0
-2х1 - х2 - х3 + 3х4=0 2х1 - 5х2 + 3х3 = 0
15) -х1 +х2 - х3 -3х4=0 16) х1 +2х2 +х3 +5х4 =0
2х1-3х2 + х3 +3х4=0 3х1 - х2 - х3 +2х4=0
-4х1-5х2 +3х3 -7х4=0 2х1 + х2 +2x3 +х4 =0
-2х1+3х2+2х3 +3х4=0 -х1 +2х2 +3х3 -х4 = 0
17) -х1 +х2 -х3+2х4=0 18) х1 +2х2 - х3 =0
2х1-3х2 +х3-5х4=0 -3х1 +х2-5х3+10х4=0
-4х1+5х2 -3х3 +9х4=0 х1 +3х2 - 3x3 +4х4 =0
х1 - х2 + х3 -2 х4=0 2х1 - х2 - х3 +7х4 = 0
19) х1 +2х2 +3х3-7х4=0 20) 3х1 +х2 -3х3 -14х4 =0
2х1-3х2 - х3 - 7х4=0 4х2+4х3 +12х4=0
3х1+3х2 - х3 +5х4=0 х1 +7х2 +5x3 +14х4 =0
4х1 +5х2 - х3 + 5х4=0 2х1 +2х2 - х3 - 6х4 = 0
21) х1 -2х2 +5х3+3х4=0 22) 2х1 -х2 +3х3 +3х4 =0
4х1-х2 +6х3 +5х4=0 3х1 - 2х2+х3 +2х4=0
х1-3х2 +7х3 +4х4=0 4х1 -3х2 +x3 +3х4 =0
3х1 -2х2 +7х3 +5х4=0 -3х1 +4х2 -х3 -6х4= 0
23) -х1 +х2 -х3-4х4=0 24) х1 -2х2 -3х3 =0
3х1+х2 - 4х3 +х4=0 2х1 +3х2+х3 -7х4=0
2х1+3х2 -2х3 -х4=0 3х1 +4х2 +x3 -10х4 =0
3х2 +х3 -2х4=0 4х1 +5х2 +х3-13х4= 0
25) 3х1 +2х2 +3х3+2х4=0 26) х1 -2х2 +х3 +7х4 =0
4х1+3х2 - 4х3 - 2х4=0 4х1 - х2+5х3 +6х4=0
-2х1-2х2 +4х3 +2х4=0 х1 -3х2 +4x3 +7х4 =0
-5х1+2х2 -3х3 =0 2х1 - х2 +х3 +6х4 = 0
27) 3х1 +х2 -3х3 =0 28) х1 -2х2 +3х3 -11х4 =0
4х2 +4х3 - 4х4=0 3х1 +х2-4х3 =0
х1+7х2 +5х3 - 6х4=0 -х1 -х2 +2x3 +2х4 =0
2х1 +2х2 - 2х3 =0 2х1 +4х2 -5х3 +8х4= 0
29) х1 +2х2 +4х3-3х4=0 30) 3х1+5х2 +2х3 =0
3х1+5х2 +6х3 - 4х4=0 4х1 +7х2+5х3=0
4х1+5х2 -2х3 +3х4=0 х1 +х2 - 4x3 =0
3х1 +8 х2 -24х3 -19х4=0 2х1+9х2 +6х3= 0
