Молек / 23

ЛАБОРАТОРНАЯ РАБОТА № 23

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ

МЕТОДОМ КЛЕМАНА И ДЕЗОРМА

Общие указания

ТЕПЛОЕМКОСТЬ

а) Теплоемкостью тела называется производная

, (1)

где – подведенное к телу или отведенное от него количество теплоты, – элементарное изменение температуры тела.

Удельная теплоемкость – теплоемкость отнесенная к единице массы тела

(2)

Вводят также теплоемкость молярную, т.е. отнесенную к 1 молю вещества

, (3)

где – число молей вещества, - молярная масса.

Очевидно из (2) и (3) видно, что

(4)

Из (1) также следует, что все три разновидности теплоемкости зависят от способа подвода или отвода теплоты и могут изменяться от 0 до +.

Из (1), (2) и (3) легко получить размерности теплоемкостей в СИ.

, и .

Используя первое начало термодинамики

(5)

подставив в (1) получим:

(6)

б) Применим это уравнение к идеальному газу. Из школьного курса физики известно для 1 моля одноатомного идеального газа:

и тогда (7)

(8)

В случае изохорного процесса (V = const) выраженное (8) равно 0 и для 1 моля можно записать:

(9)

Т.к. по закону Менделеева-Клапейрона для одного моля идеального газа pV = RT дифференцируем последнее для изобарного процесса (p = const), т.е. pdV = RdT уравнение (8) примет вид , а второе слагаемое в (6) будет равно R (для 1 моля).

. (10)

Это уравнение Роберта Майера.

в) Классическая теория теплоемкости.

Т.к. для одного моля одноатомного идеального газа , то на 1 молекулу приходится энергия:

, (11)

где – число Авогадро, – постоянная Больцмана.

Введем простейшее понятие числа степеней свободы молекулы i – это количество независимых координат, однозначно определяющее положение и конфигурацию молекулы в пространстве.

Тогда для одноатомной молекулы (материальная точка) i = 3 - это три координаты (три поступательные степени свободы), т.к. они равноправны, то на каждую степень свободы приходится энергия

(12)

По классической теории все степени свободы равноправны и, например, для двухатомной жесткой молекулы добавится еще 2 вращательных степени свободы, а при упругой связи еще две колебательных (гармонический осциллятор). В общем случае нелинейная N-атомная упругая молекула имеет 3N-6 колебательных связей, а линейная 3N-5. Колебания в молекулах возбуждаются при достаточно высокой температуре.

Величина отношения теплоемкости при постоянном давлении к теплоемкости при постоянном объеме C_P/C_V для газов играет очень большую роль при адиабатических процессах и в процессах, близких к ним. Для примера укажем, что ею, в частности, определяется скорость распространения звука в газах, от нее зависит течение газов по трубам со звуковыми скоростями и достижение сверхзвуковых скоростей в расширяющихся трубах. Всякое быстрое изменение состояния газа можно с достаточной степенью точности рассматривать как адиабатическое. При быстром сжатии газа в каком-либо сосуде наблюдается повышение температуры, при быстром расширении – понижение.

Описываемый ниже способ определения отношения удельных теплоемкостей газов C_P/C_V чрезвычайно прост при его экспериментальном осуществлении.

Пусть мы имеем стеклянный сосуд, соединенный с манометром, посредством крана сосуд может соединяться с атмосферой, и пусть первоначально в нем было атмосферное давление. Если с помощью насоса накачать в сосуд небольшое количество воздуха и закрыть кран, то давление в сосуде, конечно, повысится; но если это повышение было произведено достаточно быстро, манометрический столбик не сразу займет окончательное положение, т.к. сжатие воздуха было адиабатическим, и, следовательно, температура его повысилась. Окончательная разность уровней в манометре установится только тогда, когда температура воздуха внутри сосуда сравняется, благодаря теплопроводности стенок, с температурой окружающего воздуха.

Обозначим через абсолютную температуру окружающего воздуха, через - давление газа внутри сосуда, соответствующее показанию манометра ; совершенно ясно, что , (13)

где - атмосферное давление (конечно при этом и должны быть выражены в одинаковых единицах). Эти два параметра и характеризуют состояние газа, которое мы назовем первым состоянием газа (1 состояние: ).

Если теперь быстро открыть кран, то воздух в сосуде будет расширяться адиабатически, пока давление его не сделается равным P₀, при этом он охладится до температуры T₂ , это будет вторым состоянием газа (2 состояние: T₂, P₀). Если сразу после открытия снова закрыть кран, то давление внутри сосуда начнет возрастать вследствие того, что охладившийся при расширении воздух станет снова нагреваться до температуры окружающей среды. Возрастание давления прекратится, когда температура воздуха в сосуде сравняется с внешней температурой T₁ , это будет третьим состоянием газа (3 состояние: T₁, P₂).

Обозначим давление воздуха в сосуде в этот момент через P₂ и соответствующее показание манометра – через h₂. Ясно, что

. (14)

Т.к. переход от второго состояния к третьему состоянию произошел без изменения объема, то мы вправе применить здесь закон Шарля:

. (15)

К процессу адиабатического расширения, т.е. к переходу из первого состояния во второе может быть применен закон Пуассона, который удобно написать в следующей форме:

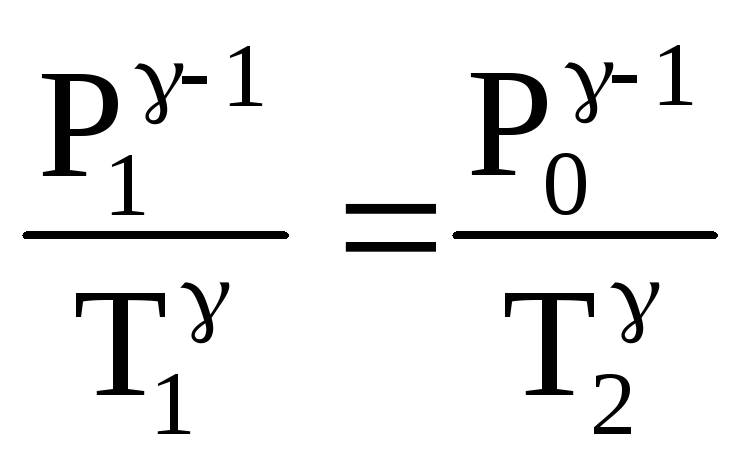, (16)

где - есть отношение удельных теплоемкостей газа при постоянном давлении и при постоянном объеме C_P/C_V (показатель адиабаты). Подставляя сюда значение P₁ из уравнения (13) и, переставляя члены, получим:

или

Т.к. и – величины малые сравнительно с единицей, то, разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получим:

, откуда

Но выражение, стоящее в левой части уравнения, есть не что иное, как . Действительно, подставив в уравнение (15) значение из уравнения (14) и разрешив его относительно , получим:

.

Следовательно, можно написать .

Откуда окончательно находим (17)

Измерения

Стеклянный баллон, герметически закрытый, соединен трубкой с водяным манометром, а другой трубкой – с ручным насосом (см. установку). Кран, вмонтированный в крышку баллона, сообщает баллон с наружным воздухом.

Поворачивают кран так, чтобы прекратить сообщение баллона с наружным воздухом. Осторожно действуя насосом, нагнетают воздух в сосуд (достаточно одного полного качка насоса) и краном перекрывают насос. После того, как давление установится, производят отсчет h₁ (разность уровней воды в обоих коленах манометра). Быстрым поворотом открывают кран, вмонтированный в крышку баллона, соединив воздух внутри баллона с наружным воздухом и тут же его опять перекрывают. При этом слышно характерное кратковременное шипение выходящего из баллона воздуха. Когда давление в манометре окончательно установится, производят второй отсчет h₂. Когда разность уровней в манометре достигнет 6 – 8 см, закрывают кран "F". Опыт следует повторить не менее 10 – 15 раз, меняя всякий раз величину h₁. Подставляя в формулу (17) значения h₁ и h₂, взятые из отдельных наблюдений, находят величину , как среднее значение всех , полученных при наблюдении.

Контрольные вопросы

1. Объясните принцип действия прибора.

2. В чём сущность метода Клемана и Дезорма?

3. Каков физический смысл универсальной газовой постоянной?

4. Как связаны между собой С_P и С_V?

5. Рассчитайте величину  для воздуха теоретически (по формуле).

6. Что называется степенью свободы? Какое число степеней свободы имеют одно-, двух- и многоатомные молекулы?

7. Дайте определение адиабатическому процессу. Какими уравнениями он описывается?

8. Что такое теплоемкость (удельная, молярная)?

9. Почему считается, что при проведении опытов присутствуют адиабатические процессы, ведь установка не теплоизолирована от окружающей среды?

Литература

1. Савельев И.В. Курс общей физики. М. Наука. 1989. §§ 87, 88, 97.

2. Савельев И.В. Курс общей физики. Том 1. М. Наука. 1989. §§ 68, 69, 72.

5