§3. Спектральный признак

Общая идея

Пусть дано однородное конечно-разностное уравнение (линейное с постоянными коэффициентами): L_hu_h=0.

В зависимости от того, является ли случай двумерным или трехмерным, будем обозначать точные и приближенные значения в узлах:

.

Заметим, что частные степенные решения можно определять в следующем виде: .

Для аппроксимации решения требуется уменьшать шаг (диаметр) сетки h. При этом числаm,n,pвозрастают. Решение же должно быть ограниченным. Это приводит к следующему необходимому признаку устойчивости:

| λ|≤1 –спектральный признак устойчивости (признак Неймана).

Пример

Рассмотрим однородное уравнение: .

а)правосторонняя схема

Разностное уравнение примет вид: .

Обозначим .

Рассмотрим частное решение в виде. Подставим его в разностное уравнение:- уравнение относительно λ.

О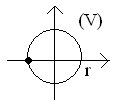бозначимS = e^iα, -∞<α<∞.

Рассмотрим уравнение V=rS(r<1).

Рассмотрим уравнение u = -V.

Таким образом, λ = 1-r+re^iα= 1-r+V. Это означает, что к окружности в плоскости (S) добавлено положительное число (1 –r)>0, что дает сдвиг в плоскости (λ) вправо:

Значит, необходимое условие спектрального признака | λ |<1 выполняется.

Рассмотрим тот же шаблон при. Плоскость (λ) тогда имеет вид:

Значит в данном случае спектральное условие

не выполняется.

б)левосторонняя схема

Разностное уравнение примет вид: .

Обозначим .

Рассмотрим частное решение в виде . Подставим его в разностное уравнение:.

Тогда:

Докажем, что | λ|>1 для любого значенияr. Действительно:

при

Значит для всех остальных значений α | λ |>1. Отсюда спектральный признак никогда не выполняется.

§4. Задача уравнения теплопроводности

Будем рассматривать одно- и двумерное уравнение (по пространственным переменным): .

Применим для решения данных уравнений сеточный метод.

1.Одномерная теплопроводность

Рассмотрим первую краевую задачу:

(10)

Физическая интерпретация:

u(x,t) – температура стержня на [0;1] (или плотность диффундирующего вещества) в точкеxв момент времениt;

φ₀, φ₁– температура стержня на концах (или плотность вещества на границе).

Обозначим область определения функции u(x,t) какD= (0;1)×(0;T).

Соответствующую сеточную область обозначим D_h= {(x_m,t_p)} – прямоугольная сетка с шагами τ иh.

Т.е. x_m=mh, t_p=pτ, m=1,2..M-1, M=1/n, p=1,2..[T/τ] – внутренние узлы.

Обозначим .

Существуют две простейшие схемы решения задачи (10).

Явная разностная схема

Схема имеет вид:

(11)

Аппроксимация

Обозначим разностное уравнение в схеме (11) как .

Рассмотрим выражение вида:

- погрешность первого порядка по τ и второго поh.

Если граничные и начальные условия аппроксимируются точно в узлах, то B_h(u)_h-B_hu_h = 0. А значит РС (11) аппроксимирует задачу (10) с указанной погрешностью.

Спектральный признак

Предполагается, что f(x,t)≡0 и ,соответственно, разностное уравнение однородно:.

Обозначим как .

Запишем разностное уравнение схемы (11) в виде:

.

Будем искать частное решение в виде: .

Подставим, сократим, получим:

.

Спектральный признак требует выполнения условия | λ |<1 или -1< λ<1.

Рассмотрим при каких значениях α выполняется первое условие:

.

Второе же условие выполняется при любых значениях r.

Таким образом, условием спектрального признака для явной РС (11) можно взять .

Устойчивость

Докажем достаточность условия для устойчивости явной РС.

Запишем разностное уравнение схемы (11) в виде:

.

Заметим, что:

При этом:

,

т.к. первый максимум определяется по все внутренним узлам, второй – по сдвинутым влево (первый = 0), четвертый – по сдвинутым вправо узлам (последний = 0).

Получим систему неравенств:

Сложив, получим:

Заметим, что , а значит.

Отсюда: -условие устойчивости.

Таким образом, из аппроксимации и устойчивости, получаем, что РС (11) сходится к решению задачи (10).

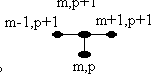
Неявная разностная схема

Схема имеет вид:

(12)

Аппроксимация

Обозначим разностное уравнение в схеме (12) как .

Рассмотрим выражение вида:

- погрешность первого порядка по τ и второго поh.

Если граничные и начальные условия аппроксимируются точно в узлах, то B_h(u)_h-B_hu_h = 0. А значит РС (12) аппроксимирует задачу (10) с указанной погрешностью.

Спектральный признак

Предполагается, что f(x,t)≡0 и ,соответственно, разностное уравнение однородно:.

Обозначим как .

Запишем разностное уравнение схемы (11) в виде:

.

Будем искать частное решение в виде: .

Подставим, сократим, получим:

.

Таким образом в неявной разностной схеме спектральный признак выполняется при любых соотношениях hи τ.