3.Метод Монте-Карло (метод статистических испытаний) для задачи Дирихле

Рассмотрим задачу (18) при f(x,y)=0:

.

Физическая интерпретация:

u(x,y) – установившаяся температура пластины, не зависящая от времени, в точке (x,y);

g(x,y) – температура на границе пластины.

Конечно-разностная схема (19) примет вид:

(23)

Сделаем следующие предположения относительно температуры u_mnв точке (x_m,y_n):

1)в точку (x_m,y_n) приходит столько же тепла, сколько и выходит из нее. Это можно записать уравнением:

2)из граничных точек приходит столько тепла, сколько и уходит в них:

, где- заданная температура в граничной точкеS_i; χ – коэффициент диффузии;p_i– некоторые коэффициенты.

В частном случае следует, что. А значит из предположения 2 получим:p_i– вероятность перехода тепла из внутреннего в граничный узел при случайном равновероятном переходе в соседние точки.

Утверждение В процессе случайных блужданий по сеткеQ_h, точка с вероятностью, равной 1, прийдет в граничную точку.

Если точка (x_m,y_n) есть граничный узелS_i0иp_i0=1, тоp_i=0, а значитu_mn=g_mnнаS_h.

Из первого соотношения следует, что если сократить его на χ и умножить на 1/h, то получим разностное уравнение Лапласа из задачи (23).

Рассмотрим некоторый внутренний узел и соединенные с ним узлы. В процессе блужданий происходит равновероятный переход в 4 соседние точки.

Таким образом, будем использовать генератор последовательностей случайных чисел из (0;1).

Обозначим ξ – равномерно распределенная случайная величина. Разобьем отрезок (0;1) на 4 равные части, с каждой из которых соотнесем свое направление. Получим равновероятный переход точки.

Получив новую точку, берем ξ, определяем переход и т.д.

Пусть M– количество выходов из внутренней точки на границу,M>>1.

Обозначим S_h={S_i}. ЕслиM_i– количество выходов из внутренних точек в граничную точкуS_i, то.

Тогда .

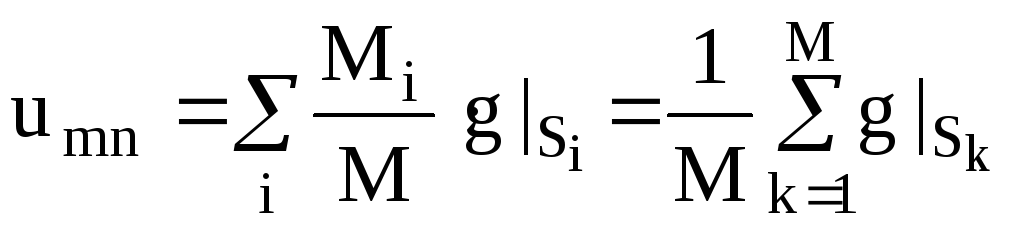Преимущество методав том, что он является простым для областей со сложной границей, его можно применять в многомерном случае, а также существует возможность вычислить значение функции в отдельно взятой точке, не вычисляя его в остальных.

Недостаток метода:рассматриваемая случайная величина не является строго равномерно распределенной с достаточной весовой точностью.

4.Проекционный метод точечных потенциалов

Продолжим рассмотрение задачи в области Q:

.

Обозначим - внешняя область. Обозначимz^m=(ξ^m, η^m) из областиQ⁺.

Последовательность {z^m}^∞- базисная, если она ограничена поверхностьюSвQ⁺, удовлетворяющей условию единственности гармонических функций вR²(т.е. если гармонические функцииu(x,y) иv(x,y) совпадают во всех точках (ξ^m, η^m), то они тождественно совпадают).

Примеры:

1)все рационалные точки некоторой окрестности (еслиuиvсовпадают в рациональных точках, то в силу непрерывности они совпадают во всей окрестности, а значит тождественно равны по теореме единственности гармонических функций)

2)все рациональные точки границы некоторой подобласти (совпадаениеuиvв рациональных точках границы означает их совпадаение на всей границе, а значит и во всей подобласти)

Потенциал простого слоя -потенциал наS, еслиR(x,y)=R₀=constнаS.

Плотность φ(x,y) и потенциал простого слояR(x,y) существуют для всякой поверхностиS, а также единственны с точностью до множителя.

Обозначим

Лемма Система {α_m(x,y)} является замкнутой и линейно независимой в L₂(S).

Доказательство

Докажем в частном случае R₀≠0.