
- •Классическая теория электропроводности металлов.
- •Вывод основных законов электрического тока в классической теории электропроводности металлов. (Закон Ома, Закон Джоуля — Ленца, Закон Видемана — Франца.
- •Самостоятельный газовый разряд и его типы (тлеющий, искровой, дуговой и коронный).
- •33. Вихревые токи. Токи Фуко.
-
Классическая теория электропроводности металлов.
Исходя
из представления о свободных электронах,
П. Друде и Х. Лоренц создали теорию
электропроводности металлов. Согласно
этой теории свободные электроны ведут
себя как молекулы идеального газа. В
промежутках между столкновениями они
движутся свободно, пробегая некоторый
путь
![]() .
Столкновения электронов осуществляется
преимущественно с ионами решетки, и это
приводит к тепловому равновесию между
электронным газом и кристаллической
решеткой. Среднюю скорость теплового
движения электронов можно произвести
по формуле:
.
Столкновения электронов осуществляется
преимущественно с ионами решетки, и это
приводит к тепловому равновесию между
электронным газом и кристаллической
решеткой. Среднюю скорость теплового
движения электронов можно произвести
по формуле:
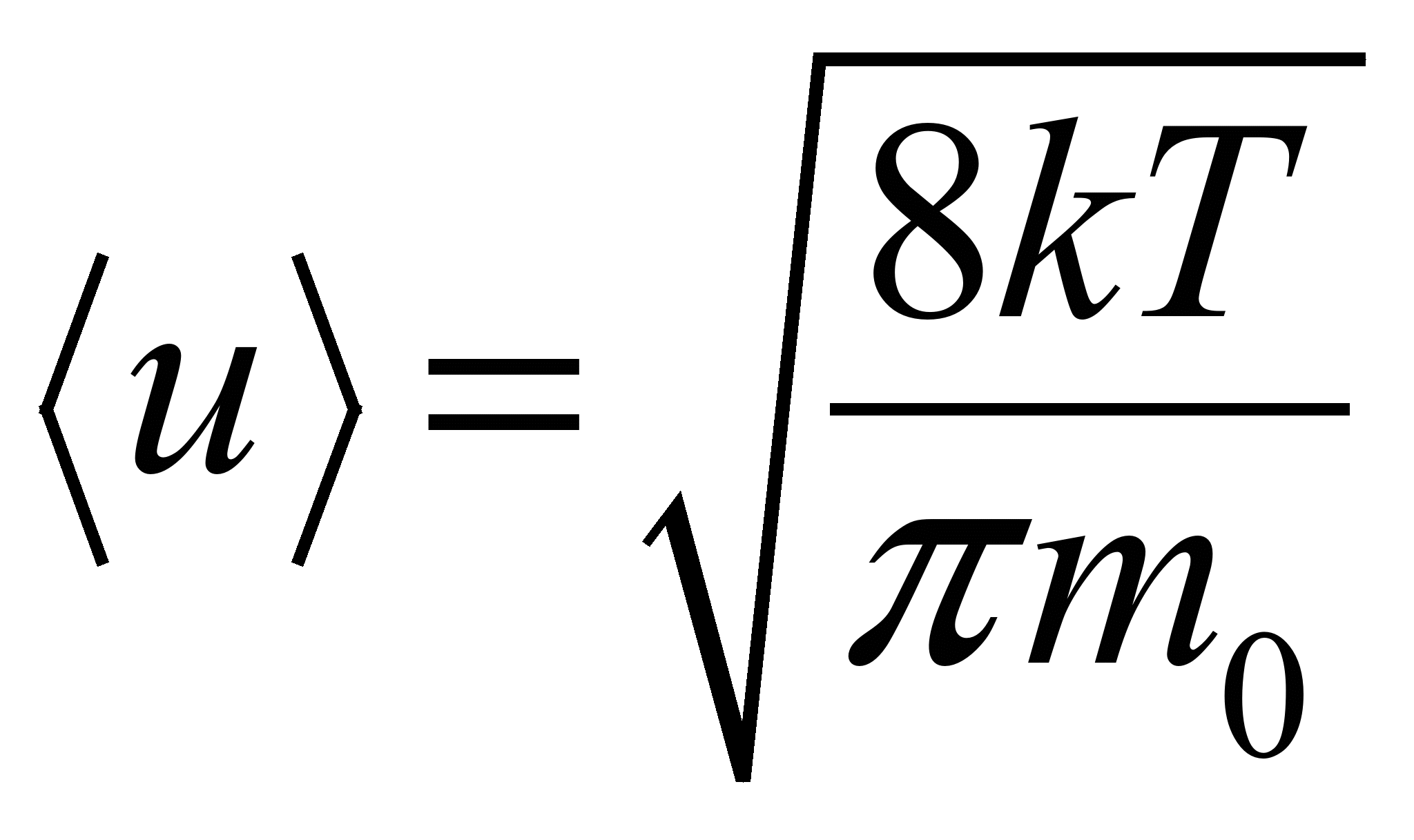 .
.
При
![]() эта
скорость порядка 105
м/с.
При включении поля на хаотическое
движение частиц накладывается
упорядоченное движение с некоторой
средней скоростью
эта
скорость порядка 105
м/с.
При включении поля на хаотическое
движение частиц накладывается
упорядоченное движение с некоторой
средней скоростью
![]() .
Ее можно оценить из выражения
.
Ее можно оценить из выражения
![]() .
(2) Предельно допустимая плотность тока
для медных проводников 107
А/м2,
а концентрация электронов
.
(2) Предельно допустимая плотность тока
для медных проводников 107
А/м2,
а концентрация электронов
![]() .
Заряд электрона равен 1.6·10-19
Кл. Подставляя все эти значения в формулу
(2) получаем, что средняя скорость
направленного движения частиц равна
.
Заряд электрона равен 1.6·10-19
Кл. Подставляя все эти значения в формулу
(2) получаем, что средняя скорость
направленного движения частиц равна
![]() .
Т.е. даже при очень больших плотностях
тока средняя скорость теплового движения
много больше средней скорости направленного
движения, вызванного электрическим
полем.
.
Т.е. даже при очень больших плотностях
тока средняя скорость теплового движения
много больше средней скорости направленного
движения, вызванного электрическим
полем.
-
Вывод основных законов электрического тока в классической теории электропроводности металлов. (Закон Ома, Закон Джоуля — Ленца, Закон Видемана — Франца.
Получим
основные законы электропроводности на
основе теории Друде- Лоренца. Согласно
этой теории при соударении электрона
с ионом кристаллической решетки
приобретенная электроном дополнительная
энергия полностью передается иону, и,
следовательно, скорость электрона
становится равной нулю. Под действием
поля электроны ускоряются и приобретают
ускорение, равное
![]() .
За время свободного пробега
.
За время свободного пробега
![]() скорость
электрона увеличивается до
скорость
электрона увеличивается до
![]() .
Считая, что скорость всех электронов
одинакова, можно записать, что время
свободного пробега электрона равно
.
Считая, что скорость всех электронов
одинакова, можно записать, что время
свободного пробега электрона равно
![]() ,
где u практически равна скорости
хаотического движения электронов.
,
где u практически равна скорости
хаотического движения электронов.
![]() .
Скорость изменяется линейно за время
свободного пробега, поэтому средняя
скорость упорядоченного движения
электронов равна
.
Скорость изменяется линейно за время
свободного пробега, поэтому средняя
скорость упорядоченного движения
электронов равна
![]() .
Плотность тока:
.
Плотность тока:
![]() .
(3) Таким образом, плотность тока
оказалась пропорциональной напряженности.
Выражение (3) можно записать в виде:
.
(3) Таким образом, плотность тока
оказалась пропорциональной напряженности.
Выражение (3) можно записать в виде:
![]() (4)
(4)
Полученная
формула выражает закон Ома в
дифференциальной форме. Здесь
![]() -
коэффициент пропорциональности,
проводимость металла.
Если бы не
было столкновений между электронами и
ионами решетки, то проводимость была
бы бесконечной
-
коэффициент пропорциональности,
проводимость металла.
Если бы не
было столкновений между электронами и
ионами решетки, то проводимость была
бы бесконечной
Получим
закон Джоуля-Ленца на основании
теории Друде-Лоренца. К концу свободного
пробега электрон приобретает кинетическую
энергию:
![]()
![]() ,
(5)
Здесь учтено, что для электрона
иметь скорость v и u статистически
независимые события, а средняя скорость
теплового движения
,
(5)
Здесь учтено, что для электрона
иметь скорость v и u статистически
независимые события, а средняя скорость
теплового движения
![]() .
Последнее слагаемое в формуле (5)
.
Последнее слагаемое в формуле (5)
![]() -
средняя кинетическая энергия теплового
движения. Т.о. в присутствии поля, электрон
приобретает дополнительную энергию
-
средняя кинетическая энергия теплового
движения. Т.о. в присутствии поля, электрон
приобретает дополнительную энергию
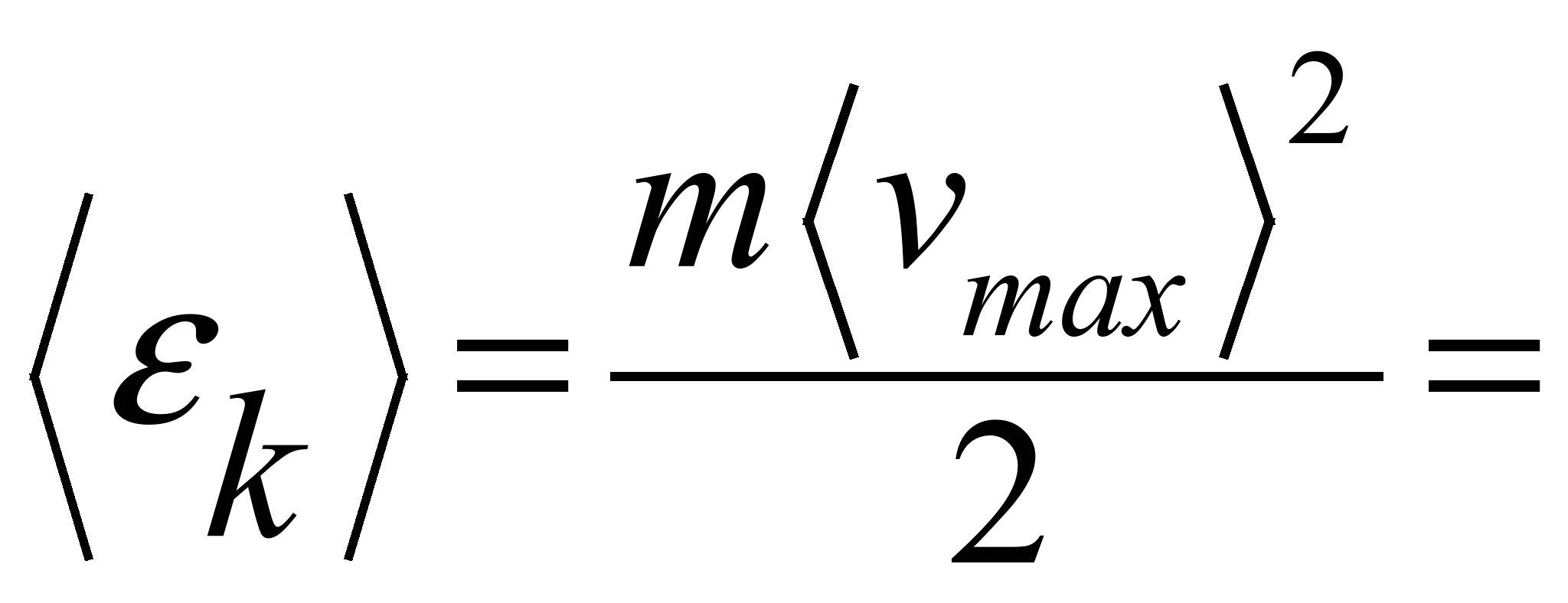
![]() .
Столкнувшись с ионом, электрон полностью
передает эту энергию кристаллической
решетке. Эта энергия идет на увеличение
внутренней энергии решетки, т.е. на
нагревание. Каждый электрон за секунду
претерпевает
.
Столкнувшись с ионом, электрон полностью
передает эту энергию кристаллической
решетке. Эта энергия идет на увеличение
внутренней энергии решетки, т.е. на
нагревание. Каждый электрон за секунду
претерпевает
![]() столкновений.
Следовательно, в единице объема за
единицу времени должно выделится тепло:
столкновений.
Следовательно, в единице объема за
единицу времени должно выделится тепло:
![]() .
Коэффициент при
.
Коэффициент при
![]() совпадает
с
совпадает
с
![]() .
Т.о.
.
Т.о.
![]() -
это и есть закон Джоуля-Ленца.
^
Закон Видемана–Франца. Видеман
и Франц установили связь между
коэффициентом теплопроводности и
электропроводности для всех металлов.
Теплопроводность металлов, как показывает
опыт, значительно выше теплопроводности
диэлектриков. Из этого следует, что
теплопроводность в металлах осуществляется
в основном не кристаллической решеткой,
а свободными электронами. Поэтому,
рассматривая электроны, как одноатомный
газ, используем формулу для коэффициента
теплопроводности газов:
-
это и есть закон Джоуля-Ленца.
^
Закон Видемана–Франца. Видеман
и Франц установили связь между
коэффициентом теплопроводности и
электропроводности для всех металлов.
Теплопроводность металлов, как показывает
опыт, значительно выше теплопроводности
диэлектриков. Из этого следует, что
теплопроводность в металлах осуществляется
в основном не кристаллической решеткой,
а свободными электронами. Поэтому,
рассматривая электроны, как одноатомный
газ, используем формулу для коэффициента
теплопроводности газов:
![]() .
Удельная теплоемкость одноатомного
газа:
.
Удельная теплоемкость одноатомного
газа:
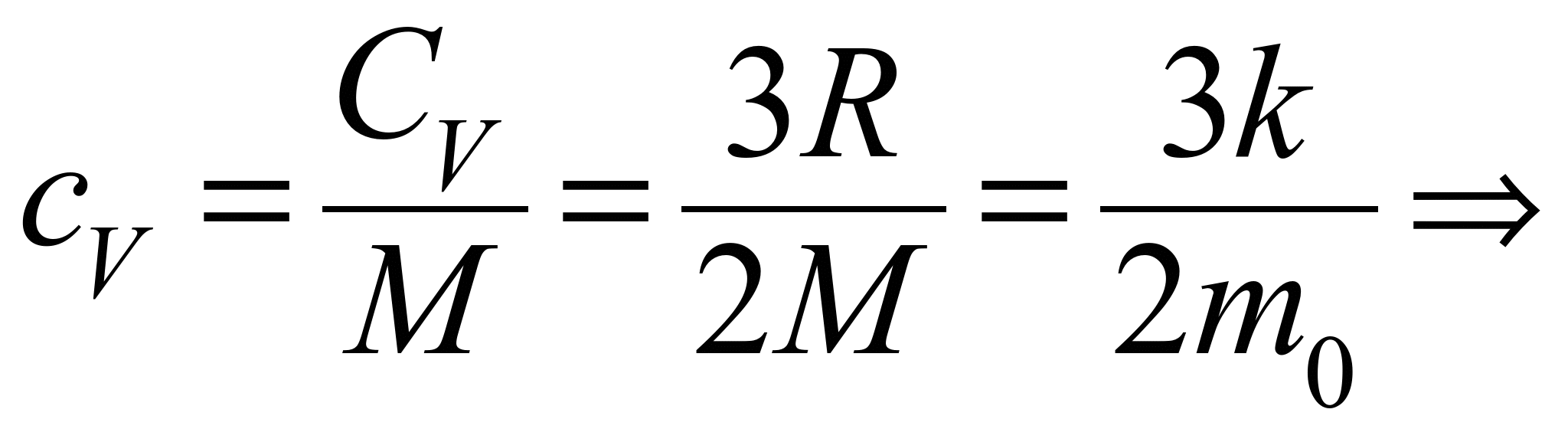
![]() .
Отношение коэффициента теплопроводности
к коэффициенту электропроводности:
.
Отношение коэффициента теплопроводности
к коэффициенту электропроводности:
![]() .
Т.о. отношение коэффициента теплопроводности
к коэффициенту электропроводности
пропорционально температуре. Это
соотношение хорошо согласуется с
экспериментальными данными. Но уточненные
Лоренцем расчеты получили другое
соотношение между
и , которое
хуже согласуется с экспериментальными
данными. Т.е. классическая теория дает
только качественное соответствие закона
Видемана –Франца.
Теплоемкость
металла можно представить как теплоемкость
решетки и теплоемкость электронного
газа. Каждый атом колеблется около
своего положения равновесия и имеет
три степени свободы. Энергия, приходящаяся
на каждую колебательную степень свободы
.
Т.о. отношение коэффициента теплопроводности
к коэффициенту электропроводности
пропорционально температуре. Это
соотношение хорошо согласуется с
экспериментальными данными. Но уточненные
Лоренцем расчеты получили другое
соотношение между
и , которое
хуже согласуется с экспериментальными
данными. Т.е. классическая теория дает
только качественное соответствие закона
Видемана –Франца.
Теплоемкость
металла можно представить как теплоемкость
решетки и теплоемкость электронного
газа. Каждый атом колеблется около
своего положения равновесия и имеет
три степени свободы. Энергия, приходящаяся
на каждую колебательную степень свободы
![]() .
Поэтому молярная теплоемкость решетки:
.
Поэтому молярная теплоемкость решетки:
![]() .
Теплоемкость электронного газа:
.
Теплоемкость электронного газа:
![]() .
Следовательно, полная теплоемкость
металла
.
Следовательно, полная теплоемкость
металла
![]() .
У диэлектриков теплоемкость обусловлена
только решеткой. Т.е. теплоемкость
металла должна быть в 1.5 раза больше
теплоемкости диэлектрика, а эксперимент
показывает, что их теплоемкости почти
одинаковы. Объяснение всех несоответствий
классической теории электропроводности
металлов с экспериментом объясняется
только квантовой теорией металлов.
.
У диэлектриков теплоемкость обусловлена
только решеткой. Т.е. теплоемкость
металла должна быть в 1.5 раза больше
теплоемкости диэлектрика, а эксперимент
показывает, что их теплоемкости почти
одинаковы. Объяснение всех несоответствий
классической теории электропроводности
металлов с экспериментом объясняется
только квантовой теорией металлов.
