54. Частные производные первого порядка.

Определение. Если существует , то он называется частной производной (первого порядка) функциипо переменнойи обозначается

Аналогично определяется частная производная по переменной y:

55. Производные от сложной функции многих переменных

Обобщим понятие сложной функции на случай функции многих переменных. Пусть дана функция 

(1)

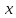аргументы, которой и– функции других переменныхи:

Если в соотношение (1) вместо 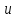иподставить их выражения черези, то в результате получим сложную функцию переменныхи:

В частном случае, если изависят только от одного переменного:то сложная функцияявляется функцией одного переменного.

56. Частные производные второго порядка

Частные производные от частных производных первого порядка называются частными производными второго порядка.

= ,=.

= ,=.

Две последние называют смешанными производными.

Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:

.

57. Теорема о смешанных производных

Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.

.

Пример. .

, ,

, ,,,

.

58. Полный дифференциал первого порядка

Функция называется дифференцируемой в точкеx₀, если ее приращение Δy(x₀,Δx) может быть представлено в виде

.

Главная линейная часть приращения Δy называется дифференциалом этой функции в точке x₀, соответствующим приращению Δx, и обозначается символом dy (x₀,Δx).

Для того, чтобы функция была дифференцируема в точкеx₀,необходимо, чтобы существовала производная , при этом справедливо равенство.

Выражение для дифференциала имеет вид

,

Где .

Свойства дифференциала:

1. , где C− постоянная;

2. ;

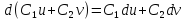3. ;

4. ;

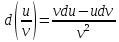59. Уравнения касательной плоскости и нормали к поверхности

Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке и которая проходит через эту точку.

Уравнение нормали к поверхности в точке имеет вид

Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке.

Из этого определения следует, что уравнение касательной плоскости к поверхности в точке имеет вид:

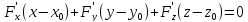
Если поверхность задана уравнением , то его можно представить в вида; тогда имеем, отсюда получаем,и. В этом случае уравнение касательной будет иметь вид

,

а уравнение нормали

Если точка поверхности является особой, то в этой точке нормальный к поверхности вектор может не существовать, и, следовательно, поверхность может не иметь нормали и касательной плоскости.

60. Градиент функции, свойства градиента

Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции и обозначается или (читается «набла у»):

.

При этом говорят, что в области D определено векторное поле градиентов.

Для нахождения градиента функции 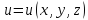в заданной точке 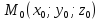используют формулу:

Свойства градиента

1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента. Это наибольшее значение производной равно .

2. Производная по направлению вектора, перпендикулярного к вектору 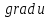, равна нулю.

61. Производная функции по направлению.

Определение. Предел отношения , если он существует, называется Производной функции Z=F(M) в точке M(X; Y) по направлению вектора L .

Обозначение. 

Если функция F(M) дифференцируема в точке М(х; у), то в точке М(х; у) существует производная по любому направлению L, исходящему из М; вычисляется она по следующей формуле:

(8)

Где Cos И Cos - направляющие косинусы вектора L.

62. Дифференциалы второго порядка, матрица Гeccе.

Определение. Пусть функция дважды дифференцируема в точке x. Дифференциалом второго порядка от функции иливторым дифференциалом в точке x называется дифференциал от ее первого дифференциала d(dy). Второй дифференциал обозначается d²y .

Теорема

Если функция у = f(x) дважды дифференцируема и х - независимая переменная, то формула для второго дифференциала имеет вид:

Квадратная симметрическая матрица порядка n, элементами которой являются частные производные целевой функции второго порядка, называется матрицей Гессе и обозначается: