
- •1. Натуральные числа.
- •1. Если функции иявляются бесконечно малыми, то функциятакже есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.
- •2. Произведение ограниченной при функции на бесконечно малую есть функция бесконечно малая.
- •3. Произведение постоянной на бесконечно малую есть бесконечно малая.
- •4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.
- •8. Первый замечательный предел. Второй замечательный предел
- •9. Критерий Коши сходимости последовательности
- •10. Предел функции, два определения.
- •12. Непрерывность функции. Разрывы первого и второго рода
- •13. Теоремы Вейерштрасса о функции непрерывной на отрезке.
- •14. Теорема о свойстве непрерывной на отрезке функции принимающей на концах отрезка значения разных знаков (Больцано-Коши).
- •15. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины.
- •16. Сравнение бесконечно больших величин. Эквивалентные бесконечно большие величины.
- •17.Применение эквивалентных бесконечно малых и бесконечно больших величин для вычисления пределов.
- •18 Производная функции. Механический и геометрический смысл производной.
- •Тангенс угла наклона касательной прямой
- •Скорость изменения функции
- •19 Свойства производных. Правила дифференцирования
- •20 Производные элементарных функций.
- •21 Производная сложной функции. Производная обратной функции
- •22 Дифференциал функции. Геометрический смысл
- •23 Приближенное выражение приращения функции через дифференциал.
- •24 Производная высшего порядка.
- •Формула Тейлора
- •34. Асимптоты
- •35. Выпуклость и вогнутость графика функции. Точки перегиба
- •43.Замена переменной и интегрирование по частям в определенном интеграле.
- •44.Приложение интегралов. Площадь плоской фигуры.
- •45.Несобственные интегралы 1-го и 2-го рода. Сходимость интегралов.
- •51.Предел последовательности n-мерных точек.
- •52. Предел функции многих переменных, два определения.
- •В этом случае пишут илипри.
- •53. Непрерывные функции многих переменных.
- •54. Частные производные первого порядка.
- •60. Градиент функции, свойства градиента
- •63. Необходимые условия локального экстремума дифференцируемой функции многих переменных. Стационарные точки.
- •64. Достаточное условие экстремума функции многих переменных.
- •65. Комплексные числа. Алгебраическая и тригонометрическая формы комплексного числа. Формула Эйлера. Вычисление корней многочленов.
- •66. Дифференциальные уравнения, основные понятия.
- •67. Дифференциальные уравнения с разделяющимися переменными.
- •68. Линейные уравнения первого порядка.
- •69. Линейные дифференциальные уравнения с постоянными коэффициентами второго порядка.
12. Непрерывность функции. Разрывы первого и второго рода
Определение непрерывности функции в точке.
Функция f(x) называется непрерывной
в точке ![]() ,
если предел слева равен пределу справа
и совпадает со значением функции в
точке
,
если предел слева равен пределу справа
и совпадает со значением функции в
точке ![]() ,
то есть
,
то есть ![]() .
.
Следствие.
ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ ТОЧКАХ.
Определение устранимого разрыва первого рода.
В
точке ![]() функция
имеет устранимый разрыв первого
рода, если предел слева равен пределу
справа, но они не равны значению функции
в точке ,то есть
функция
имеет устранимый разрыв первого
рода, если предел слева равен пределу
справа, но они не равны значению функции
в точке ,то есть![]() .
.
Определение неустранимого разрыва первого рода (точка скачка функции).
В
точке ![]() функция
имеет неустранимый разрыв первого
рода, если пределы слева и справа НЕ
равны, то есть
функция
имеет неустранимый разрыв первого
рода, если пределы слева и справа НЕ
равны, то есть![]() .
Точку
.
Точку![]() в
этом случае называют точкой скачка
функции.
в
этом случае называют точкой скачка
функции.
Определение разрыва второго рода (бесконечный разрыв).
В
точке ![]() функция
имеет разрыв второго рода, если либо
предел слева
функция
имеет разрыв второго рода, если либо
предел слева![]() ,
либо предел справа
,
либо предел справа![]() ,
не существует или бесконечен.
,
не существует или бесконечен.
13. Теоремы Вейерштрасса о функции непрерывной на отрезке.
Т1.Если
функция f непрерывна на
отрезке [a,b] , то f ограниченна на отрезке
[a,b], т.е. существует такое число М, что
 ,
при всех
,
при всех
Т2.Если f непрерывна на [a, b], то она достигает на нем своей верхней и нижней грани.
14. Теорема о свойстве непрерывной на отрезке функции принимающей на концах отрезка значения разных знаков (Больцано-Коши).
Теорема
Больцано-Коши. Если
функция ![]() является
непрерывной на отрезке
является
непрерывной на отрезке![]() и
принимает на концах этого отрезка
неравные между собой значения, то
есть
и
принимает на концах этого отрезка
неравные между собой значения, то
есть![]() ,
,![]() ,
то на этом отрезке функция принимает и
все промежуточные значения между
,
то на этом отрезке функция принимает и
все промежуточные значения между![]() и
и![]() .
.
Следствие 1. Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то на этом отрезке есть хотя бы одна точка, в которой функция обращается в нуль.
15. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины.
Определение
1.
Функции ![]() и
и ![]() называются
бесконечно малыми величинами одного
порядка малости, если
называются
бесконечно малыми величинами одного
порядка малости, если .
Определение
2. Функция
.
Определение
2. Функция ![]() называется
бесконечно малой величиной более
высокого порядка малости, чем
называется
бесконечно малой величиной более
высокого порядка малости, чем ![]() ,
если
,
если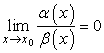 .
Определение
3.
Функция
.
Определение
3.
Функция ![]() называется
бесконечно малой величиной более низкого
порядка малости, чем
называется
бесконечно малой величиной более низкого
порядка малости, чем ![]() ,
если
,
если .
Определение
4.
Функция
.
Определение
4.
Функция ![]() называется
бесконечно малой величиной
называется
бесконечно малой величиной ![]() го
порядка малости относительно
го
порядка малости относительно ![]() ,
если
,
если .
Определение
5.
Функции
.
Определение
5.
Функции ![]() и
и ![]() называются
несравнимыми бесконечно малыми
величинами, если
называются
несравнимыми бесконечно малыми
величинами, если  не
существует и не равен
не
существует и не равен ![]() .
Определение
6.
Две бесконечно малые величины
.
Определение
6.
Две бесконечно малые величины ![]() и
и ![]() называются
эквивалентными, если
называются
эквивалентными, если  .
.
16. Сравнение бесконечно больших величин. Эквивалентные бесконечно большие величины.
17.Применение эквивалентных бесконечно малых и бесконечно больших величин для вычисления пределов.



18 Производная функции. Механический и геометрический смысл производной.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

Геометрический и физический смысл производной
