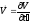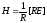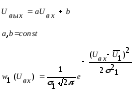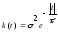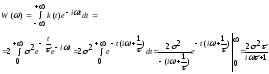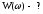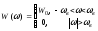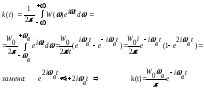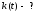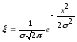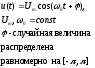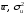Zadachi
.docx№15(9). Дано: a, Р1(t=0)=1, P2(t=0)=0
Найти: Р1(t), P2(t)/
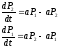
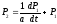
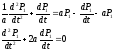
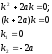
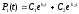
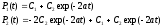
Константы С1 и С2 находим из начальных условий: Р1(t=0)=1, P2(t=0)=0
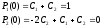
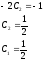
Ответ

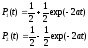
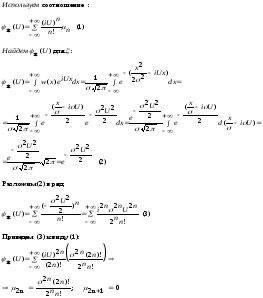
Стат. Радиофизика
|
№11(2) Дано:
|
|
|
|
_________
|
|
____
|
№13(5) Дано:
|
|
|
|
_______
|
№14(6) Дано:
|
|
|
|
|
||
|
№16(10) Дано:
|
|
|
|
Доказать:
|
||
_______
_______
|
№12(3) Дано: Случайный процесс:
|
|
|
Найти:
Доказать:
|
-
Два одинаковых LC контура связаны общей емкостью. Показать, что нормальные моды колебаний описываются формулами
 при
при
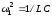 и
и
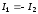 при
при
 .
.
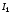 -
ток в первом контуре,
-
ток в первом контуре,
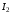 -
ток во втором контуре.
-
ток во втором контуре.
Решение
C
C
i1
i2
i3
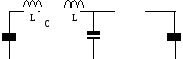
i1=i3+i2, i3=i1-i2 – закон Киргофа
Падение напряжения на катушке
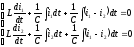
Дифференцируем по t
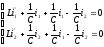
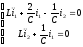
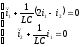
1 случай. I1=I2
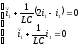
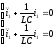
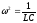 - уравнение
гармонического осциллятора
- уравнение
гармонического осциллятора
1 случай. I1=-I2
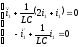
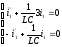
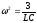 - уравнение
гармонического осциллятора
- уравнение
гармонического осциллятора
-
№1 За сколько времени звуковые колебания пройдут расстояние l между точками 1 и 2, если температура воздуха между ними меняется линейно от Т1 до Т2? Скорость звука в воздухе
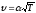 ,
α – постоянная.
,
α – постоянная.
Решение:
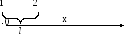
Введём координаты:
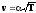 (1)
(1)
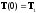 (2)
(2)
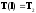 (3)
(3)
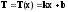 (4)
(4)
Cначала подставим (2), а потом и (3) в выражение (4)
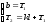 и
и
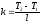
Конкретный вид
Т(х) :
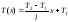 (5)
(5)
Пусть
 (6)
(6)
Подставим (5) в (1)
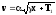 (7)
(7)
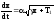 (8)
(8)
Решаем (8)
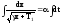
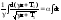
 (9)
Здесь С
обозначает некоторую произвольную
константу.
(9)
Здесь С
обозначает некоторую произвольную
константу.
Начальное условие для t=t(x)
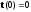 (10)
(10)
Подставим (10) в (9)

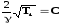 (11)
(11)
Подставим (11) в
(9), получим конкретный вид
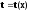
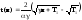
Время прохождения расстояния l
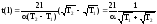
-
№2 Уравнение плоской звуковой волны имеет вид
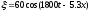 ,
где ξ – в мкм, t – в секундах, х – метрах.
Найти: а) отношение амплитуды смещения
частиц среды к длине волны; б) амплитуду
колебаний скорости частиц и ее отношение
к скорости распространения волны; в)
амлитуду колебаний относительной
деформации среды и ее связь с амплитудой
колебаний относительной скорости
частицы среды.
,
где ξ – в мкм, t – в секундах, х – метрах.
Найти: а) отношение амплитуды смещения
частиц среды к длине волны; б) амплитуду
колебаний скорости частиц и ее отношение
к скорости распространения волны; в)
амлитуду колебаний относительной
деформации среды и ее связь с амплитудой
колебаний относительной скорости
частицы среды.
Решение:
а) В общем виде
уравнение плоской звуковой волны имеет
вид
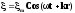 ,откуда находим амплитуду смещения
частиц
,откуда находим амплитуду смещения
частиц
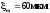
Фаза волны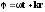 ,
где
,
где
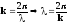
Откуда находим,
что отношение амплитуды смещения частиц
среды к длине волны равно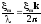 (1)
(1)
Из уравнения плоской звуковой волны k=5.3
Подставляя численные данные в (1), окончательно получим
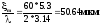
б) Скорость частиц

где -60*1800=108000 мкм/c=108 м/с – амплитуда скорости Um
скорость волны находим из условия φ=const или 1800t-5.3x=const , откуда
x=(1800t-const)/5.3
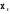 - скорость волны
- скорость волны
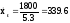 м/с
м/с
Искомое отношение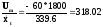
в)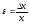 ;
;
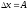 ;
; 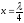 ;
; 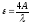 =2*10
-4.
=2*10
-4.

№3
Плоская электромагнитная волна падает
нормально на поверхность плоскопараллельного
слоя толщины l из немагнитного вещества,
диэлектрическая проницаемость которого
экспоненциально падает от значения
 1
на передней поверхности до
1
на передней поверхности до
 2
на задней. Найти время распространения
данной фазы волны через этот слой.
2
на задней. Найти время распространения
данной фазы волны через этот слой.
Решение:
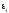 - диэлектрическая
проницаемость вверху пластинки.
- диэлектрическая
проницаемость вверху пластинки.
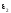 - диэлектрическая
проницаемость внизу пластинки
- диэлектрическая
проницаемость внизу пластинки
Общий вид
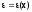
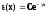 (1)
(1)
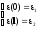 (2)
(2)
Из соотношения (2) определим γ и С
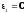
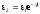

 (3)
(3)
Фазовая скорость электромагнитной волны
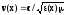 В нашем случае
среда немагнитная, поэтому μ=1
В нашем случае
среда немагнитная, поэтому μ=1
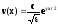 где
с – скорость света в вакууме
где
с – скорость света в вакууме
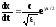 (4)
(4)
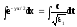
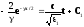 (5)
(5)
Для определения
константы С1
используем начальное условие
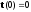 ,
подставив его в (5), получим
,
подставив его в (5), получим
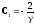 ,
поэтому
,
поэтому
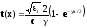 ,
а искомое время
,
а искомое время

-
№4 Линейно поляризованный световой пучок падает на поляризатор, вращающийся вокруг оси пучка с угловой скоростью w = 21 рад/с. Найти световую энергию, проходящую через поляризатор за один оборот, если поток энергии в падающем пучке Ф0 = 4,0 мВт.
Решение:
Согласно закону
Малюса,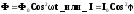
Тогда энергию,
проходящую через поляризатор за один
оборот, т.е. за один период ,
определим следующим выражением
,
определим следующим выражением
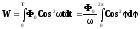
Здесь введено обозначение φ=ωt
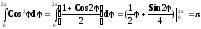
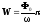
-
№5 При падении естественного света на некоторый поляризатор проходит h1 = 30 % светового потока, а через два таких поляризатора - h2 =13,5 %. Найти угол j между плоскостями пропускания этих поляризаторов.
Если при прохождении через поляризатор свет становится частично поляризованным и частично поглощается, то можно связать входящий и выходящий поток уравнением:
I1 = a I0 || , где а – коэффициент поглощения пластинки поляризатора , а I0 || составляющая входящего светового потока, параллельная оси поляризатора; т.к. свет естественный то
I0 || + I0 ┴ = I0 и I0 || = I0 ┴ ; отсюда I0 || = I0 /2;
I1 = a I0 /2.
h1= I1/ I0 = a/2 ; => a = h1 / 2;
Для второй пластинки, используя закон Малюса:
I2 = a I1 cos2 j = a ∙ a ∙ (I0 / 2) ∙ cos2 j => I2 / I0 = (a2 / 2)∙ cos2 j = h2 = 2 h12 ∙ cos2 j
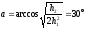
-
№6 На поверхность воды под углом Брюстера падает пучок плоскополяризованного света. Плоскость колебаний светового вектора составляет угол j = 45° с плоскостью падения. Найти коэффициент отражения.

Дано: В общем случае коэффициент отражения равен:

φ=45°
 (1)
(1)
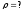
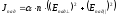
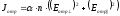
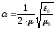
Для естественного
света
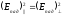 .
.
В данном случае
свет плоскополяризован, разложим его
на составляющие
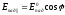 ,
,
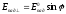 ,
где φ – угол между плоскостью поляризации
падающего плоскополяризованного света
и плоскостью падения,
,
где φ – угол между плоскостью поляризации
падающего плоскополяризованного света
и плоскостью падения,
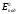 -
модуль вектора электрической напряжённости
падающего света. Если свет падает под
углов Брюстера, то отражённый свет
плоскополяризован в плоскости
перпендикулярной плоскости падения,
т.е.
-
модуль вектора электрической напряжённости
падающего света. Если свет падает под
углов Брюстера, то отражённый свет
плоскополяризован в плоскости
перпендикулярной плоскости падения,
т.е.
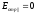 .
.
Формулы Френеля:
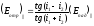
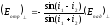 (2)
(2)
Таким образом получаем:
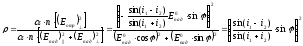 (3)
(3)
Из (3) получаем:
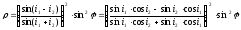
Т.к. свет падает
под углом Брюстера, то
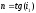 и
и
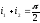 .
Если учесть, что
.
Если учесть, что
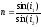 .
Далее, с учётом:
.
Далее, с учётом:
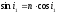 ,
,
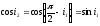 ,
имеем:
,
имеем:
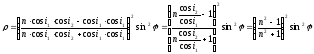
Таким образом, коэффициент отражения плоскополяризованного света при падении под углом Брюстера равен:
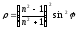
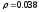
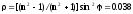
-
№7 Электромагнитная волна с частотой w распространяется в разреженной плазме. Концентрация свободных электронов в плазме равна n0. Пренебрегая взаимодействием волны с ионами плазмы, найти зависимость:
а) диэлектрической проницаемости плазмы от частоты;
б) фазовой скорости от длины волны l в плазме.
Решение:
В изотропной
нелинейной среде
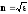 ε=1+χ, где χ – диэлектрическая
восприимчивость, которая является
коэффициентом в соотношении P=χε0Е
, где Р – поляризованность. Т.е. дипольный
момент единицы объёма.
ε=1+χ, где χ – диэлектрическая
восприимчивость, которая является
коэффициентом в соотношении P=χε0Е
, где Р – поляризованность. Т.е. дипольный
момент единицы объёма.
Т.о.,
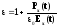 (1)
(1)
Где Рx
–проекция вектора Р на ось x,
вдоль которой совершаются колебания
вектора Е, известно, что
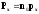 (2)
(2)
где n0 – концентрация диполей.
Рx – проекция дипольного момента отдельного диполя.
Рассмотрим простейшую модель невзаимодействующих друг с другом атомов. При наличии внешнего поля Е электронное облако смещается относительно практически неподвижного ядра, и возникает дипольный момент P=ql l – вектор, проведённый из центра облака к ядру.
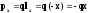 (3)
(3)
Подставим (2) и (3) в (1)
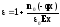 (1.а)
(1.а)
Задача сводится к нахождению x(t). Для этого запишем уравнение движения
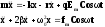 (4)
(4)
Где ω0=k/m 2β=r/m fm=qEm/m
Для теории дисперсии имеет смысл не общее, а частное решение уравнения (4)
X=a Cos(ωt-φ)
Подстановка этого решения в (4) даёт возможность с помощью векторной диаграммы найти значения амплитуды и фазы, а именно:
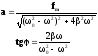
Для анализа решения ограничимся простейшим случаем, когда 2βω<<(ω0 2-ω2), т.е. если ω<ω0, то
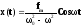 (5)
(5)
Подставляя (5) в (1.а) окончательно получаем
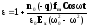
Учтём также, что qEmCosωt= -qEx
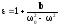 где
где
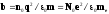
Где N0 - концентрация электронов, здесь учтено, что q=ze , m=zme , N0=zn0
В случае
плазмы(электроны свободные ) собственная
частота колебаний электронов ω0=0,
поэтому диэлектрическая проницаемость
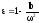 ,
где
,
где

Здесь me – масса электрона.
Фазовая скорость
равна
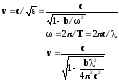
-
№8 Найти концентрацию свободных электронов ионосферы, если для радиоволн с частотой v = 100 МГц ее показатель преломления n = 0,90.
Решение:
Для плазмы ω0=0,
поэтому
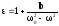 принимает
вид
принимает
вид
 где
где
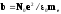
ε=n2
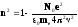
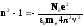

-
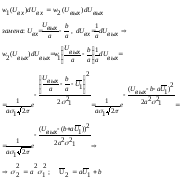
№9 Найти зависимость между групповой u и фазовой v скоростями для следующих законов дисперсии:
a)
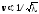
б)
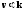
в)

Здесь l, k и w - длина волны, волновое число и круговая частота.
Решение:
А)
Для решения применим формулу Релея
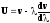
Пусть
 ,
где а – некоторая произвольная константа
,
где а – некоторая произвольная константа
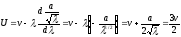
Б) По определению
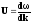 ,
где
,
где
 ,
тогда
,
тогда
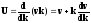
Пусть
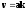 ,
где а- некоторая постоянная , в этом
случае
,
где а- некоторая постоянная , в этом
случае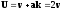
В) Пусть
 ,
где а – постоянная, тогда
,
где а – постоянная, тогда
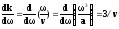
Поэтому
групповая скорость
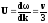
-
№10 В некоторой среде связь между групповой и фазовой скоростями электромагнитной волны имеет вид uv=c2 где с - скорость света в вакууме. Найти зависимость диэлектрической проницаемости этой среды от частоты волны, e(w).
Решение: Исходим
из выражения для групповой скорости
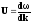 ,
где
,
где
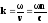 ,
учитывая, что
,
учитывая, что
 ,
перепишем k
в виде
,
перепишем k
в виде
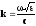
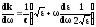 (1)
(1)
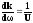
 (2)
(2)
Приравнивая (1) и (2), получаем
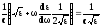
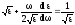 /умножая
полученное выражение на ε, получим
/умножая
полученное выражение на ε, получим
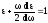
Разделяя переменные ε и ω получаем
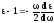
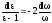
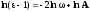 ,
где А-константа.
,
где А-константа.
Потенцируя последнее выражение , получаем
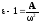
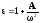
Задачи к государственному экзамену по курсу «Электродинамика»
-
Вычислить напряженности электрического и магнитного полей, создаваемых зарядом q , движущимся в постоянной скоростью v.
Определим потенциалы поля, создаваемого
одним точечным зарядом, совершающим
заданное движение по траектории
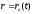 .
.
Согласно формулам запаздывающих
потенциалов поле в точке наблюдения
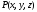 в момент времени t
определяется состоянием движения заряда
в предшествующий момент времени
в момент времени t
определяется состоянием движения заряда
в предшествующий момент времени
 ,
для которого время распространения
светового сигнала из точки нахождения
заряда
,
для которого время распространения
светового сигнала из точки нахождения
заряда
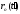 в точку наблюдения Р как раз совпадают
с разностью
в точку наблюдения Р как раз совпадают
с разностью
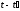 .
.
Пусть
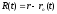 -радиус
вектор от заряда е в точку наблюдения
Р; вместе с
-радиус
вектор от заряда е в точку наблюдения
Р; вместе с
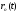 он является заданной функцией времени.
он является заданной функцией времени.
 -
момент времени, предшествующий времени
наблюдения заряда t.
-
момент времени, предшествующий времени
наблюдения заряда t.
Тогда момент
 определяется уравнением.
определяется уравнением.
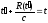 (1)
(1)
Для каждого значения t это уравнение
имеет всего один корень

В системен отсчета, в которой в момент
времени
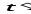 частица покоится, поле в точке наблюдения
в момент t дается просто кулоновским
потенциалом, т.е.
частица покоится, поле в точке наблюдения
в момент t дается просто кулоновским
потенциалом, т.е.
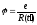 , А
= 0 (2)
, А
= 0 (2)
Выражения для потенциалов в произвольной
системе отсчета мы получим теперь,
написав такой 4-вектор, который бы при
скорости V = 0 давал для
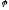 и А значения (2). Замечая, что
скорость согласно (1)
и А значения (2). Замечая, что
скорость согласно (1)
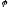 из (2) можно написать также в виде
из (2) можно написать также в виде
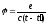
находим, что искомый 4-вектор есть
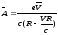 и
и
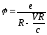 -потенциалы
Лиенара- Вихерта.
-потенциалы
Лиенара- Вихерта.

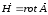
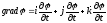
-радиус-вектор
точки наблюдения.
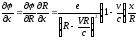
аналогично для y и для z.
В результате:
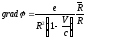
С
помощью этих формул не представляет
труда вычислить поля
 и
и
 :
:
Опуская промежуточные вычисления, приведём получившийся результат:
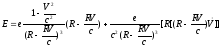 ,
,
где