57. Критерий согласия Пирсона

 Критерий согласия Пирсона (χ²) применяют для проверки гипотезы о соответствии эмпирического распределенияпредполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.

Использование критерия χ² предусматривает разбиение размаха варьированиявыборкина интервалы и определения числа наблюдений (частоты) n_j для каждого из e интервалов. Для удобства оценокпараметров распределения интервалы выбирают одинаковой длины.

Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10 ÷ 15, при n = 200 e = 15 ÷ 20, при n = 400 e = 25 ÷ 30, при n = 1000 e = 35 ÷ 40.

Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалы с частотой n_j ≥ 2.

Статистикой критерия Пирсона служит величина ,   (3.91) где p_j - вероятность попадания изучаемой случайной величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x). При вычислении вероятности p_j нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до -∞, а последний - до +∞.

Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле (3.91) величины с критическим значением χ²_α, найденным по табл. VIприложения для уровня значимости α и числа степеней свободы k =e₁ - m - 1. Здесь e₁ - число интервалов после объединения; m - число параметров, оцениваемых по рассматриваемой выборке. Если выполняется неравенство χ² ≤ χ²_α   (3.92) то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.

Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ² другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).

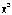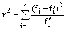Критерий согласия Пирсона – один из основных:где k – число групп, на которые разбито эмпирическое распределение,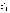– наблюдаемая частота признака в i-й группе,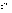– теоретическая частота.

58. Критерий согласия Колмагорова

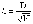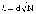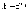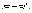Критерий Колмогорова l основан на определении максимального расхождения между накопленными частотами и частостями эмпирических и теоретических распределений: или, где D и d – соответственно максимальная разность между накопленными частотамии накопленными частостямиэмпирического и теоретического рядов распределений; N          – число единиц совокупности. Рассчитав значение l, по таблице Р(l) определяют вероятность, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность Р(l) может изменяться от 0 до 1. При Р(l)=1 происходит полное совпадение частот, Р(l)=0 – полное расхождение. Если l принимает значения до 0,3, то Р(l)=1. Основное условие использования критерия Колмогорова – достаточно большое число наблюдений.

Критерий согласия Колмогорова

Последовательность действий при проверке гипотезы о законе распределения при помощи критерия согласия Колмогорова следующая.

1. Построить вариационный ряд и график эмпирической функции распределения F*(x), где эмпирическая функция распределения определяется формулой

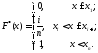
2. По виду графика F*(x) выдвинуть гипотезу:

, ,

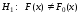где F₀(x) – функция гипотетического закона распределения.

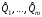
3. Используя метод моментов или максимального правдоподобия, определить оценки неизвестных параметров гипотетического закона распределения.

4. Рассчитать 10−20 значений функции F₀(x) и построить ее график в одной системе координат с функцией F*(x).

5. По графику определить максимальное отклонение по модулю между

функциями F*(x) и F₀(x).

.

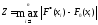6. Вычислить значение критерия Колмогорова

.

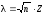7. Из таблицы распределения Колмогорова выбрать критическое значение 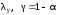, здесь α – заданный уровень значимости (α = 0,05 или 0,01).

8. Если λ > λ_γ , то нулевая гипотеза H₀ отклоняется, в противном случае нет оснований ее отклонить.