Глава1. Проблема аппроксимации

§1. Полиномиальная апппроксимация

Постановка задачи

Из теорем математического анализа известно, что всякая непрерывная на отрезке [a;b] функцияf(x) может быть хорошо приближена полиномомP_n(x).

Теорема Вейерштрасса:

Однако эта теорема не дает ответа на вопрос о существовании хорошего интерполяционного полинома для заданного множества точек {( x_i ,y_i)}.

x	x0	…	xn
y	y0	…	yn

Пусть функцияf(x) известна только в узлах некоторой сеткиx_i, т.е. задана таблицей:  (x_k≤x_k+1)

Задача нахождения значений функции:

a) между узлами () –задача интерполяции

б) вне узлов () –задача экстраполяции

Теорема:

Для всякой дискретной функции f(x), заданной предыдущей таблицей существует многочленP_n(x) степениn, совпадающий в узлах с этой функцией (P_n(x_k)=y_k ) и он единственен.(1)

Доказательство

Будем искать этот полином в виде: P_n(x)=a₀+a₁x+..+a_nxⁿ.

Запишем условие (1) в виде системы:

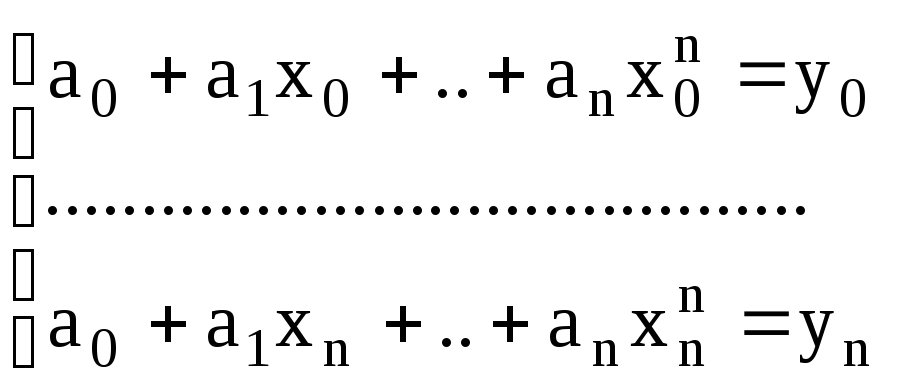(2)

Будем считать, что все узлы – разные, т.е x_k<x_k+1.

В данной системе неизвестные – a_k. Определитель системы – отличный от нуля определитель Вандермонда:

Т.о. решение системы (2) существует, а значит существует многочлен P_n(x).

Докажем его единственность. Предположим противное: существует Q_n(x):

. Тогда полиномP_n(x)-Q_n(x) равен 0 в (n+1) точкеP_n(x)-Q_n(x)≡0P_n(x)≡Q_n(x). Что и требовалось доказать.

Определение ПолиномP_n(x) – интеполяционный полином для функцииf(x).

Пример РунгеРассмотрим функциюf(x)=.

т.е. является аналитической функцией.

Рассмотрим на [-1;1] ее интерполяционный многочлен

(для значений по равномерным узлам): P_n(x_k)=.

Cвозрастаниемnмногочлен также возрастает,

увеличивая аксиляции колебаний.

§2. Интерполяционный полином в форме Лагранжа

Из системы (2) получим систему следующего вида:

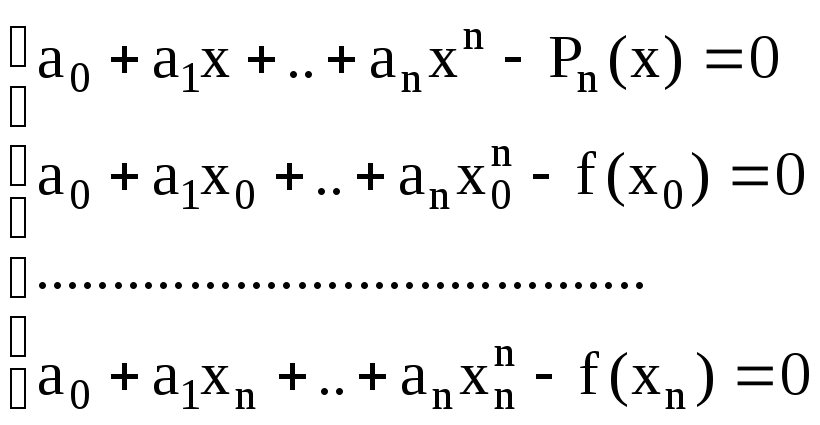(3)

Будем считать неизвестными a₀,a₁..a_n , -1.

Полученная система имеет (n+1) порядок. Ее нетривиальное решение из предыдущей теоремы существует, следовательно, ее определитель равен 0 (иначе решение (3) было бы нулевым).

Разложим этот определитель по последнему столбцу:

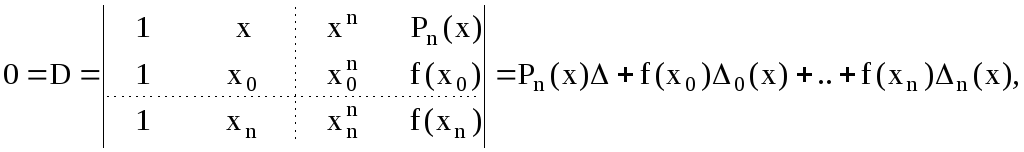
где - многочленыn-ой степени,.

Перпишем последнее равенство в виде:

где.

Заметим, что:

1) - многочленn-ой степени

2)

3)

Следовательно, многочлен определяется единственным образом.

Рассмотрим следующий многочлен (n+1)ой степени:

Обозначим .

Заметим, что:

Т.о. =, т.е. интерполяционный полином имеет вид:

- интерполяционный полином Лагранжа

Погрешность интерполяции

Представим функцию f(x) в виде: f(x)=P_n(x)+R_n(x), где R_n(x) – погрешность интерполяции. Заметим, что R_n(x) зависит от свойств f(x) (так если f(x) линейна, то R_n(x)≡0 при n>2).

Будем считать априорно, что а

Запишем погрешность в виде: R_n(x)=kω_n+1(x)+φ(x).

Тогда φ(x)=f(x)-P_n(x)- kω_n+1(x) и φ(x_k)=0, . (4)

Выберем k из условия φ(x’)=0, где x’ – точка, в которой оценивается погрешность:

Из уравнения φ(x’)=0 получим: .

При таком выборе k φ(x’)и обращается в ноль в (n+2) точках: x₀…x_n,x’.

Тогда по т. Ролля обращается в ноль в по крайней мере (n+1) точке. И т.д.

По т. Ролля имеет хотя бы один нуль. Т.е.

Т.о. из (4) получим:

.

Тогда , а значит, т.к. точкаx’ была выбрана произвольно.