
Билет18
Теорема 2. Пусть Х1, Х2 – независимые дискретные случайные величины,
![]() ,
,
![]() ,
тогда
,
тогда
![]() (4)
(4)
Доказательство. Представим событие Ax = {Х1+Х2 = x} в виде суммы несовместимых событий
Ax = å(Х1 = xi; Х2 = x – xi).
Так как Х1, Х2 – независимые то P(Х1 = xi; Х2 = x – xi) = P(Х1 = xi) P(Х2 = x – xi), тогда
P(Ax) = P(å(Х1 = xi; Х2 = x – xi)) = å(P(Х1 = xi) P(Х2 = x – xi)),
что и требовалось доказать.
Билет 19
Теорема 3. Если независимы случайные величины Х1, ..., Хn, то независимы также функции от этих случайных величин Y1 = f1(Х1), ...,Yn = fn(Хn).
Распределение Пирсона (c2-распределение). Пусть Х1, ..., Хn – независимые нормальные случайные величины с параметрами а = 0, = 1. Составим случайную величину
![]() .
.
Закон распределения
случайной величины
![]() называется
называется
![]() -распределением
(распределением Пирсона) с
степенями свободы.
-распределением
(распределением Пирсона) с
степенями свободы.
Ранее нами была найдена плотность распределения квадрата нормальной случайной

Написанное
выражение соответствует плотности
распределения c2
с числом степеней свободы n
= 1. Получим плотность распределения при
n
= 2. Пусть
![]() –
независимые нормально распределенные
случайные величины: Хi
N(0,1),
i
= 1,2. Так как Х1,
Х2
независимы,
то по теореме, сформулированной ранее
независимы также
–
независимые нормально распределенные
случайные величины: Хi
N(0,1),
i
= 1,2. Так как Х1,
Х2
независимы,
то по теореме, сформулированной ранее
независимы также
![]() .
.
Воспользуемся
теоремой свёртки: n
= 2,
![]() ,
тогда для t
> 0
,
тогда для t
> 0
![]()
Таким образом,
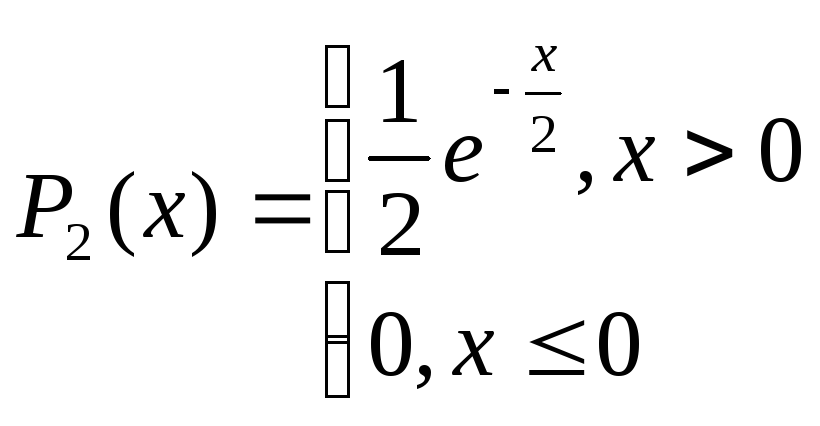
Можно показать,
что плотность
![]() для х > 0 имеет вид
для х > 0 имеет вид
![]() ,
где kn
– некоторый коэффициент для выполнения
условия
,
где kn
– некоторый коэффициент для выполнения
условия![]() .
При n
®
¥
распределение Пирсона стремится к
нормальному распределению.
.
При n
®
¥
распределение Пирсона стремится к
нормальному распределению.
Пусть Х1,
Х2,
…, Хn
N(a,),
тогда случайные величины
![]()
N(0,1).
Следовательно, случайная величина
N(0,1).
Следовательно, случайная величина
![]() имеет
2
распределение с
степенями свободы.
имеет
2
распределение с
степенями свободы.
Распределение Пирсона табулировано и используется в различных приложениях математической статистики (например, при проверке гипотезы о соответствии закона распределения).
Распределение Стьюдента (t-распределение)
Пусть Х0,
Х1,
…,Х
– независимы и Хi
~ ~N(0;σ),
σ>0,
тогда
случайная величина
 имеет по определению t-распределение
c
степенями свободы. Плотность распределения
Стьюдента имеет вид
имеет по определению t-распределение
c
степенями свободы. Плотность распределения
Стьюдента имеет вид
![]() .
.
Если ν → ∞, то распределение Стьюдента стремится к нормальному распределению.
График плотности распределения симметричен относительно прямой х = 0. По виду он напоминает нормальное распределение, но он более «пологий», с утяжеленными хвостами.
Обозначим F(x,
σ)
– функцию распределения случайной
величины t.
Если Хi
~ N(0;σ),
то случайные величины
![]() также независимы и Yi
~ N(0,
1). Тогда
также независимы и Yi
~ N(0,
1). Тогда
 .
.
Таким образом, t-распределение не зависит от параметра σ.
Аналогично
предыдущему можно показать, что если
Xi
– независимы, и Хi
~ N(a;σ),
то распределение Стьюдента имеет также
величина
 .
.
Если
Хi
~ N(0,
1), i
=1, …,,
то получим, что распределение Стьюдента
имеет случайная величина
 ,
где
,
где
![]() имеет
2-распределение.
имеет
2-распределение.
Распределение Стьюдента табулировано и используется в различных приложениях математической статистики (например, при проверке гипотезы о равенстве средних).
Распределение Фишера (F-распределение)
Пусть
Х0,
Х1,
…, Хn1,
Хn1+1,
…, Хn1+n2
– независимые
нормально распределенные случайные
величины Хi
~ N(0;σ),
i
= 1,2, …, n1+n2.
Тогда случайная величина имеет распределение Фишера со степенями
свободы n1,
n2.
Распределение Фишера также не зависит
от параметра ,
т.е.
имеет распределение Фишера со степенями
свободы n1,
n2.
Распределение Фишера также не зависит
от параметра ,
т.е.
![]() .
.
Если Xi – независимые и Хi ~ N(a;σ), то
 имеет распределение
Фишера.
имеет распределение
Фишера.
Положим = 1, получим, что распределение Фишера имеет случайная величина
![]() ,
,
где
![]() –
случайные величины, имеющие распределение
–
случайные величины, имеющие распределение
![]() .
.
При больших n1, n2 распределение Фишера приближается к нормальному.
Распределение Фишера табулировано и используется в различных приложениях математической статистики (например, при проверке гипотезы о равенстве дисперсий).
