Tablichny_protsessor3

Матричные операции

Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы.

1.Дайте новому рабочему листу имя "Матрицы".

2.Введите матрицы М и N в блоки А1 :С2 и Е1 :G2. ,

В блок А4:С5 введите табличную формулу {= А1:С2 + Е1:G2}. Ввод формулы завершите нажатием клавиш <Ctrl>+<Shift>+<Enter>.

3.Дайте диапазонам А1:С2 и Е1:G2 имена М и N. В блок Е4:G5 введите табличную формулу {= М + N }.

4.Вычислите линейную комбинацию матриц 2М- N в блоке А7:С8.

Проверьте результаты: ,

5.Математические функции для работы с матрицами:

МОПРЕД — вычисление определителя матрицы;

МОБР — вычисление обратной матрицы;

МУМНОЖ— перемножение матриц;

ТРАНСП — транспонирование.

Откройте справку Excel, запишите в тетрадь синтаксис этих функций.

!!!Произведение матриц может быть вычислено, если количество столбцов умножаемой матрицы равно количеству строк матрицы множителя. Если матрица А имеет размерность , а матрица В имеет размерность , то матрица С, полученная умножением матрицы А на матрицу В, будет иметь размер .

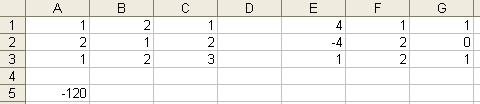
6.Вычислить определитель и обратную матрицу для исходной матрицы

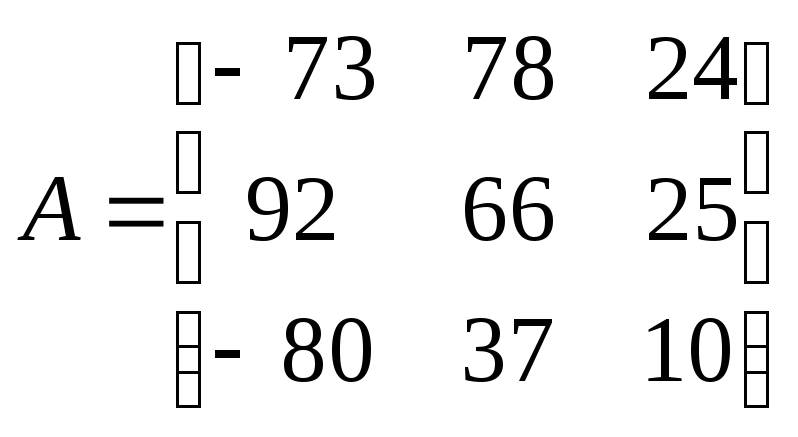
П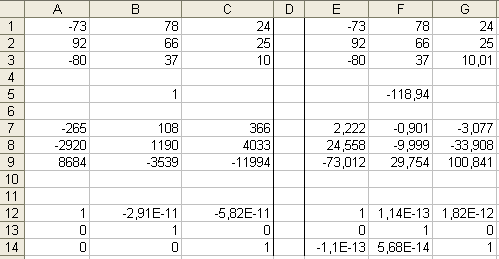роверить правильность вычисления обратной матрицы умножением ее на исходную. Повторить эти действия для той же матрицы, но с элементом

A1:C3 – исходная матрица

В5 – определитель матрицы

А7:С9 – обратная матрица

А12:С14 - проверка

7.Даны матрицы 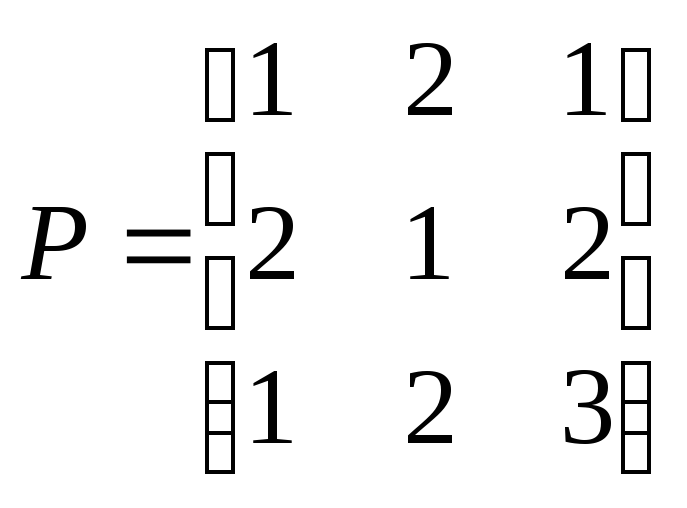и 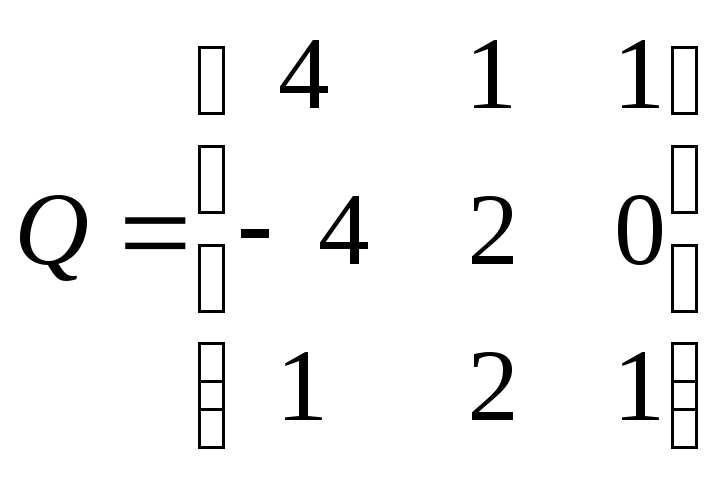. Вычислить определитель коммутатора этих матриц . Все вычисления должны быть записаны в одной ячейке.

8.Дана матрица . Вычислить матрицу , где - операция транспонирования, - единичная матрица.

9.С помощью функций работы с матрицами удобно решать системы линейных уравнений вида :

.

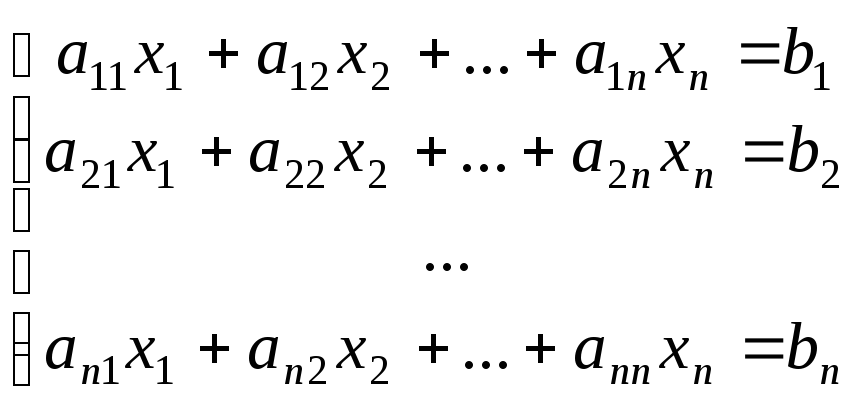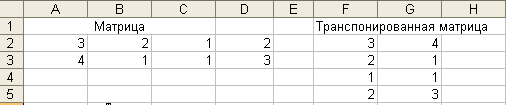
Такую систему в матричном виде можно записать как , где,,.

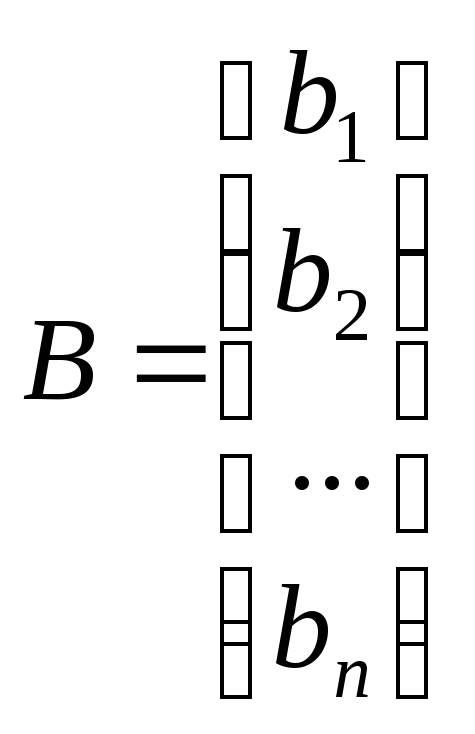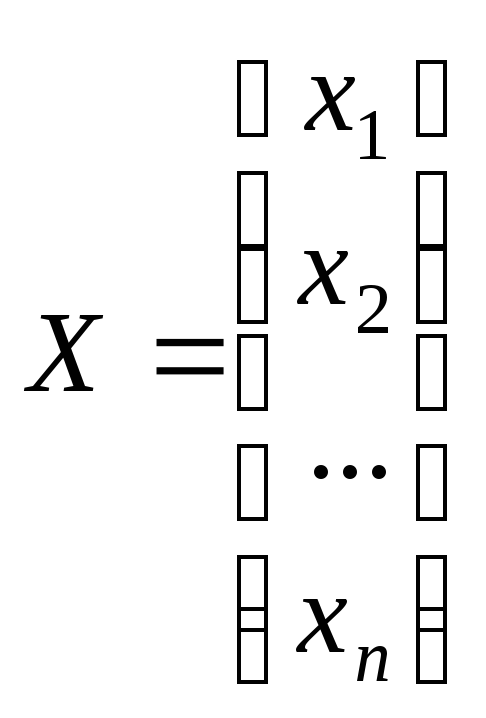Решением этой системы будет , где - обратная матрица.

Решите системы уравнений:

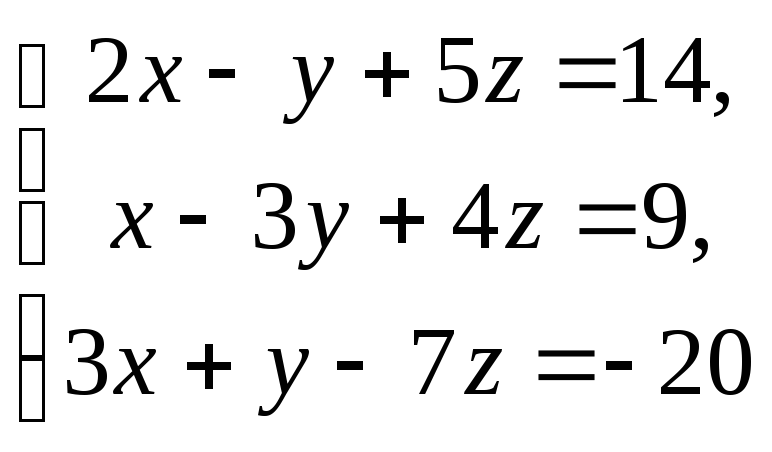
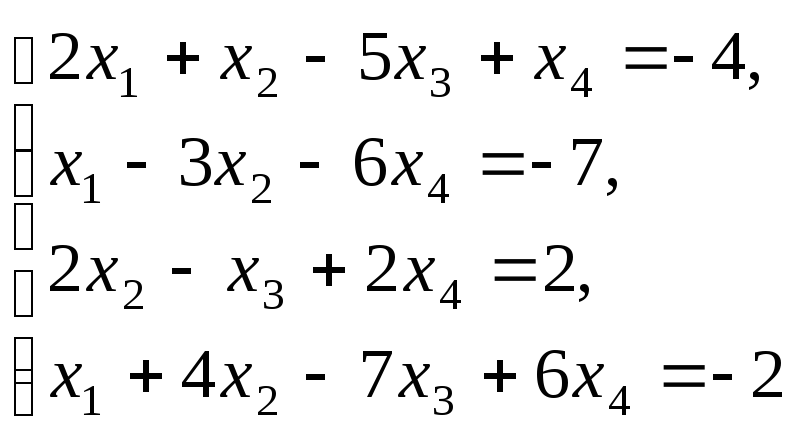
1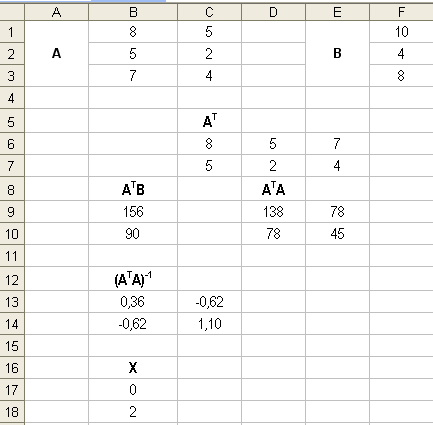0.Для решения системы линейных уравнений с неизвестными используют следующий алгоритм:

1.Найти произведение .

2.Найти произведение .

3.Найти обратную матрицу .

4.Найти вектор Х: .

Решите системы уравнений:

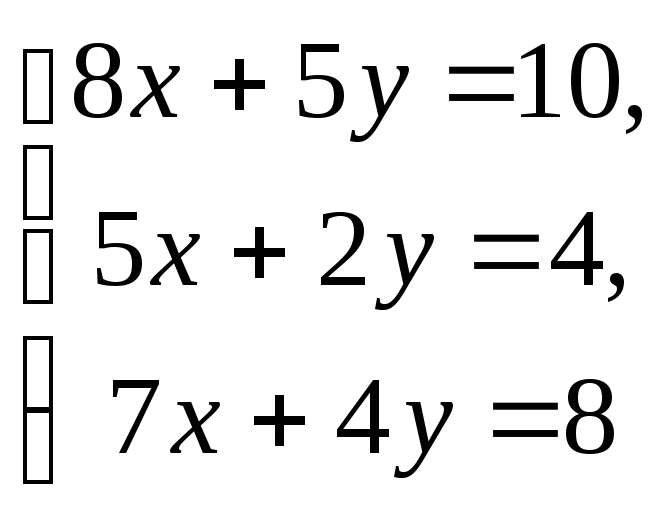
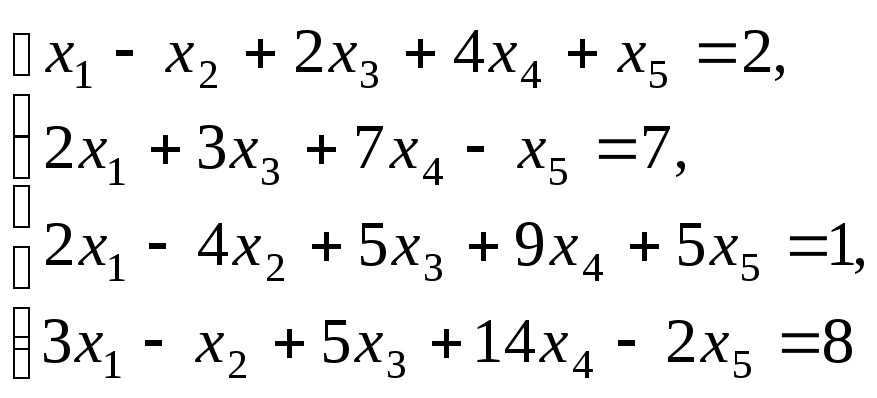
11.Решите задачи:

а) Предприятие ежесуточно выпускает четыре вида изделий, их производственно-экономические показатели приведены в таблице:

Вид изделия, условный номер	Количество выпускаемых изделий, шт.	Расход сырья, кг/изд.	Норма времени изготовления, ч/изд.	Стоимость изделия, ден. ед/изд.
	N	s	t	p
1	20	5	10	30
2	50	2	5	15
3	30	7	15	45
4	40	4	8	40

Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени T и стоимость Р выпускаемой продукции предприятия.

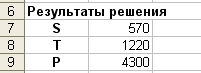
Обратите внимание на то, что требуемые показатели можно определить как скалярные произведения вектора количества выпускаемой продукции на три других вектора, например,

б) Предприятие выпускает три вида продукции из сырья трех типов. Характеристики производства приведены в таблице.

Вид сырья	Расход сырья по видам продукции, вес. ед./изд			Запас сырья вес. ед.
	1	2	3
1	6	4	5	2400
2	4	3	1	1450
3	5	2	3	1550

Требуется определить возможный объем выпуска каждой продукции при заданных запасах сырья.

Указание: Решение задачи сводится к решению системы трех уравнений с тремя неизвестными, которыми и являются возможный объем выпуска каждой продукции.