Потери в диэлектриках. Основные понятия. Диэлектрическими потерями называют электрическую мощность, затрачиваемую на нагрев диэлектрика, находящегося в электрическом поле.

Потери энергии в диэлектриках наблюдаются как при переменном, так и припостоянномнапряжении, поскольку в технических материалах обнаруживается сквознойток утечки, обусловленный электропроводностью. При постоянном напряжении, когда нет периодической поляризации, качество материала характеризуется значениямиудельного объемного и удельного поверхностного сопротивлений, которые определяют значение R_из(сопротивление изоляции).

При воздействии переменного напряжения на диэлектрик в нем кроме сквозной электропроводности могут проявляться другие механизмы превращения электрической энергии в тепловую. Поэтому, качество материала недостаточно характеризовать только сопротивлением изоляции.

В инженерной практике чаще всего для характеристики способности диэлектрика рассеивать энергию в электрическом поле используют угол диэлектрических потерь, а также тангенс этого угла.

Углом диэлектрических потерь δ называют угол, дополняющий до 90⁰угол сдвига фаз φ между током и напряжением в емкостной цепи.

В случае идеального диэлектрика вектор тока в такой цепи опережает вектор напряжения на угол 90⁰, при этом угол δ равен нулю. Чем больше рассеивается в диэлектрике мощность, тем меньше угол сдвига фаз φ и тем больше угол диэлектрических потерь δ и его функция tg δ.

Тангенс угла диэлектрических потерь входит в формулу для рассеиваемой в диэлектрике мощности, поэтому этой характеристикой пользуются чаще.

Эквивалентная схема конденсатора с диэлектриком, обладающим потерями, составляется с таким расчетом, чтобы активная мощность, расходуемая в данной схеме, была равна мощности, рассеиваемой в диэлектрике конденсатора, а ток был бы сдвинут относительно напряжения на тот же угол, что и в рассматриваемом конденсаторе. Обычно конденсатор с потерями заменяют идеальным конденсатором с параллельно включенным активным сопротивлением (параллельная схема) или конденсатором с последовательно включенным сопротивлением (последовательная схема). Эквивалентные схемы не дают объяснения механизма диэлектрических потерь и введены условно для упрощения расчётов.

Параллельная и последовательная эквивалентные схемы представлены на рис. П.1. Там же даны соответствующие диаграммы токов и напряжений. Обе схемы эквивалентны друг другу, если при равенстве полных сопротивлений Z₁= Z₂=Zравны соответственно их активные и реактивные составляющие. Это условие будет соблюдено, если углы сдвига тока относительно напряжения равны и значения активной мощности одинаковы.

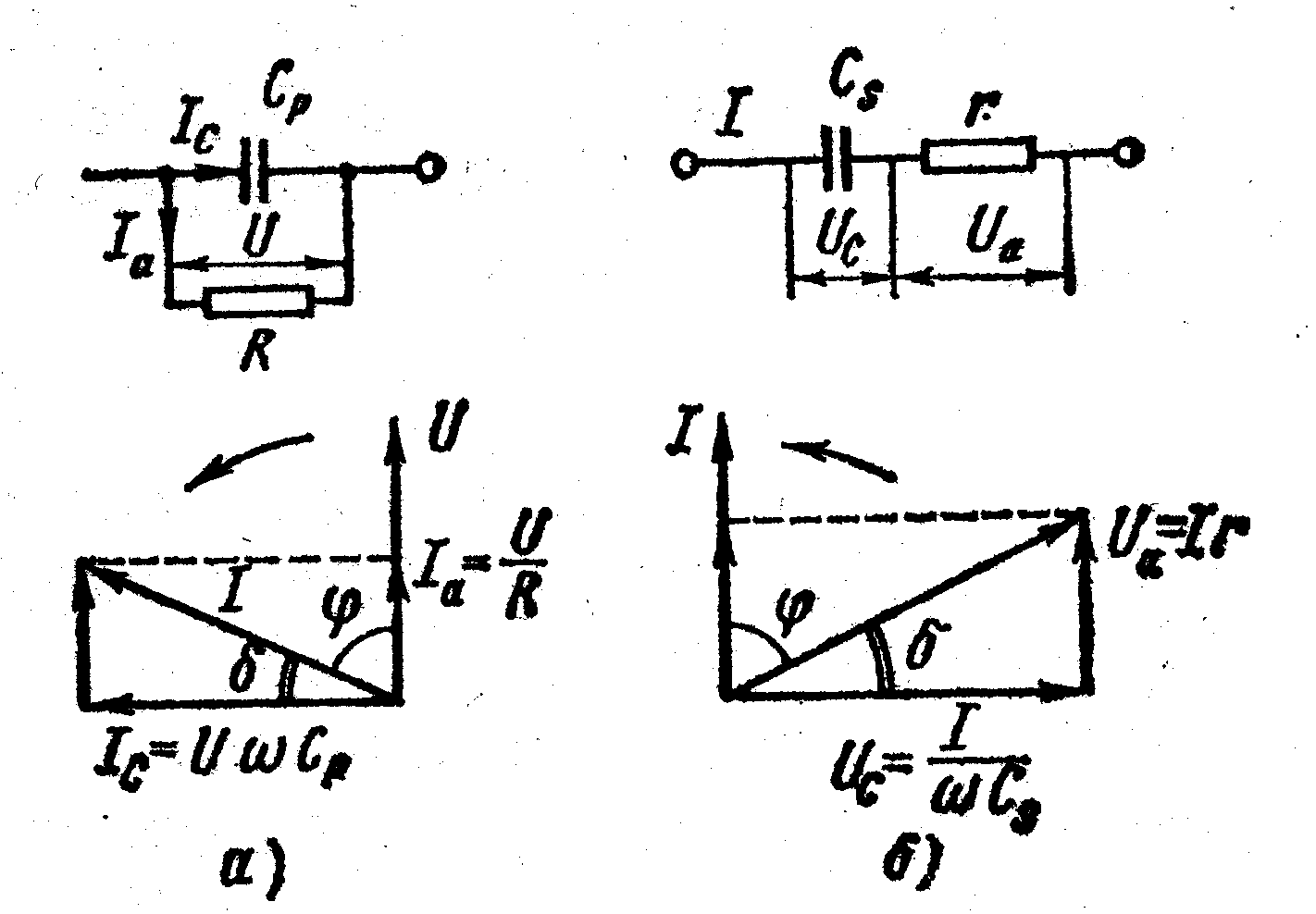
Рис. П.1. Параллельная (а) и последовательная (б) эквивалентные схемы диэлектрика с потерями и векторные диаграммы для них.

Для параллельной схемы из векторной диаграммы

tg δ = I_a / I_c = 1/(ωС_pR); (П.1)

P_a = UI_a = U²ωС_р tg δ; (П.2)

для последовательной схемы

, (П.3)

(П.4)

Приравнивая выражения (П.2) и (П.4), а также (П.1) и (П.3), найдем соотношения между C_pи C_sи между R и r:

(П.5)

(П.6)

Для доброкачественных диэлектриков можно пренебречь значением tg по сравнению с единицей в формуле (П.5) и считать C_pC_s=С. Выражения для мощности, рассеиваемой в диэлектрике, в этом случае будут также одинаковы у обеих схем:

, (П.7)

где Р, выражено в Вт; U - в В; ω - в рад/с; С - в Ф. Следует отметить, что при переменном напряжении в отличие от постоянного емкость диэлектрика с большими потерями становится условной величиной и зависит от выбора той или иной эквивалентной схемы. Отсюда и диэлектрическая проницаемость материала с большими потерями при переменном напряжении также условна.

Для большинства диэлектриков параметры эквивалентной схемы зависят от частоты. Поэтому, определив каким-либо методом значения емкости и эквивалентного сопротивления для данного конденсатора при некоторой частоте, нельзя использовать эти параметры для расчета угла потерь при другой частоте. Такой расчет справедлив только в отдельных случаях, когда эквивалентная схема имеет определенное физическое обоснование. Так, если для данного диэлектрика известно, что потери в нем определяются только потерями от сквозной электропроводности в широком диапазоне частот, то угол потерь конденсатора с таким диэлектриком может быть вычислен для любой частоты, лежащей в этом диапазоне, по формуле (П.1). Потери в таком конденсаторе определяются выражением

(П.8)

Если же потери в конденсаторе обусловлены главным образом сопротивлением подводящих и соединительных проводов, а также сопротивлением самих электродов (обкладок), например, тонким слоем серебра в слюдяном или керамическом конденсаторе, то рассеиваемая мощность в нем возрастет с частотой пропорционально квадрату частоты:

. (П.9)

Из выражения (п.9) можно сделать вывод: конденсаторы, предназначенные для работы на высокой частоте, должны иметь по возможности малое сопротивление как электродов, так и соединительных проводов и переходных контактов.

В большинстве случаев механизм потерь в конденсаторе сложный и его нельзя свести только к потерям от сквозной электропроводности или к потерям в контакте. Поэтому параметры конденсатора необходимо определять при той частоте, при которой он будет использован.

Диэлектрические потери, отнесенные к единице объема диэлектрика, называютудельными потерями. Их можно рассчитать по формуле

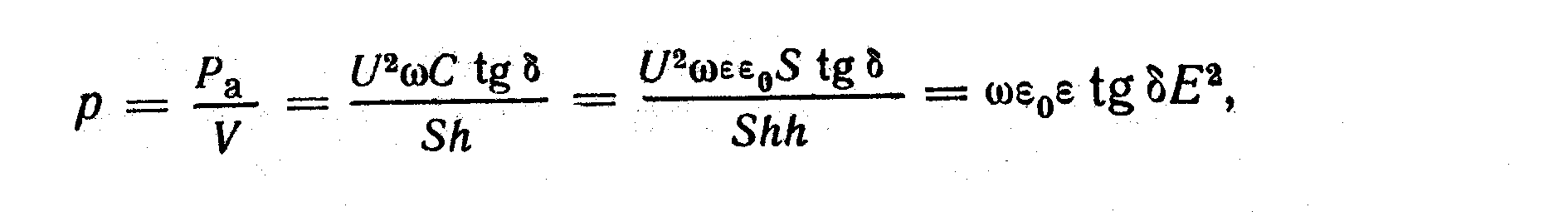
(П.10)

где V — объем диэлектрика между плоскими электродами, м³, Е— напряженность электрического поля, В/м.

Произведение ε tgδ =ε" называют коэффициентом диэлектрических потерь.

Из выражения (П.10) следует, что при заданных частоте и напряженности электрического поля удельные диэлектрические потери в материале пропорциональны коэффициенту потерь.

Приложение 2.

Таблица П.2.1 Обозначение конденсаторов по виду диэлектрика.

Обозначение конденсатора

Тип конденсатора по виду диэлектрика

К10 К15 К20 К21 К22 К23 К31 К32 К40 К41 К42 К50 К51 К52 К53 К54 К60 К61 К71 К72 К73 К75 К76 К77

Керамические на номинальное напряжение ниже 1600 В То же, на номинальное напряжение 1600 В и выше Кварцевые Стеклянные Стеклокерамические Стеклоэмалевые Слюдяные малой мощности Слюдяные большой мощности Бумажные на напряжение до 2 кВ с фольговыми обкладками То же, на напряжение 2 кВ и выше с фольговыми обкладк. Бумажные с металлизированными обкладками Электролитические фольговые алюминиевые Электролитические фольговые танталовые, ниобиевые и др. Электролитические объёмно-пористые Оксидно-полупроводниковые Оксидно-металлические Воздушные Вакуумные Плёночные полистирольные Плёночные фторопластовые Плёночные полиэтилентерефталатные Плёночные комбинированные Лакоплёночные Плёночные поликарбонатные

Таблица П.2.2 Электроизоляционные свойства полярных диэлектриков.

Материал		tg	 Ом*м	Eпр МВ/м	Рабочие температурыС
Поливинилхлорид Оргстекло Лавсан Нейлон, капрон Фторопласт-3 Силиконы	3,5 – 4,5 2,8 – 3,5 3,0 – 3,5 5 – 6 3,5 3,5	0,2 – 0,5 0,02-0,05 0,002 0,06 0,04 0,01-0,003	1012 1011 1012 10 9 1018 1014	10 – 50 18 – 40 100 20 13 – 15 15 - 25	-35 / +80 -80 / +70 -80 / +200 -40 / +200 -195 / +130 -70 / +250

Таблица П2.3. Характеристики плёнок, применяемых в микроэлектронике.

Материал	Применяемая толщина, мкм		tg при f = 1 кГц	Eпр МВ/м
Диоксид кремния (SiO2) Оксид кремния (SiO) Оксид тантала (TaO5) Нитрид кремния (SiN) Оксид алюминия (Al2O3)	0,05 – 1,5 0,3 – 3,0 0,05 – 0,25 0,5 – 1,0 0,04 - 0,3	4 9 – 12 20 - 50 5 - 10 8 - 10	0,001 – 0,04 0,01 – 0,03 0,01 – 0,5 0,003 – 0,01 0,002 – 0,01	300 100 – 300 100 - 200 до 1000 200 - 600

Лабораторная работа № 3.