Московский технический университет связи и информатики

Курсовая работа по

Теоретической механике

Выполнил:

студент группы УИ0301

Гудим А.С.

Преподаватель:

Фирсанов В.В

Москва 2004г.

Задача 4.2.19.: Две пары ступенчатых колес движутся по заданному закону S(t). Радиусы колес заданы. Определить в момент времени t1=2 c угловую скорость и угловое ускорение колеса 2, скорость и ускорение груза Р и точки В.

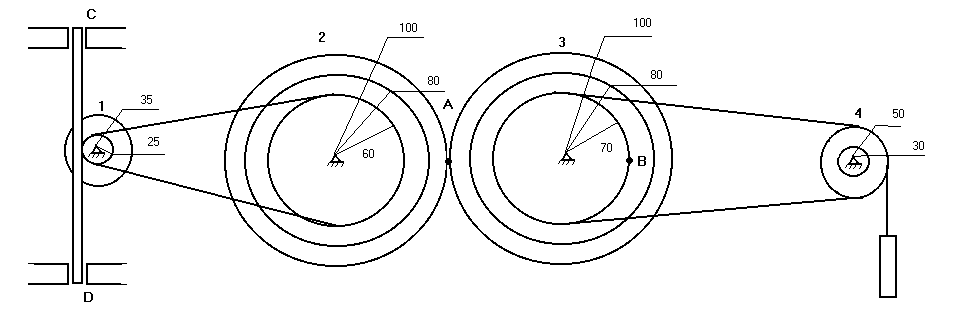
R11=25 мм.

R12=35 мм.

R21=60 мм.

R22=80 мм.

R23=100 мм.

R31=30 мм.

R32=50 мм.

R41=70 мм.

R42=80 мм.

R43=100 мм.

t1=2 c. Решение:

S(t)= ; v=S’(t)= ;a=v’(t)= . v(t1)=19 м/с; a=18 м/.

w2-? e2-?

vP-? aP-? w1= v/R12= 19/0.035=543 рад/с; e1=a/R12=18/0.035=514 рад/.

vB-? aB-? w2= w1R11/R21=543(0.025)/0.06=226 рад/с; е2= e1R11/R21=514(0.025)/0.06=214 рад/.

w4= w2R23/R43=226 0.1/0.1=226 рад/с; e4=e2R23/R43=214 рад/.

vB= w4R41=226 0.07=15.8 м/с; =R41= 3575 м/; =e4R41=15 м/.

aB= =3575 м/.

w3= w4R41/R32=316 рад/с; e3= e4R41/R23=300 рад/.

vP=w3R32=w4R41=15.8 м/c; aP=e3R23=e4R41= 15 м/.

Ответ: w2= 226 рад/с; е2= 214 рад/; vB=15.8 м/с; aB= 3575 м/; vP=15.8 м/c; aP= 15 м/.

Задача 5.7.6.: Пластина вращается вокруг неподвижной оси по закону =f1(t). По пластине вдоль линии движется точка М согласно закону ее относительного движения S= f2(t). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1=0.5 c.

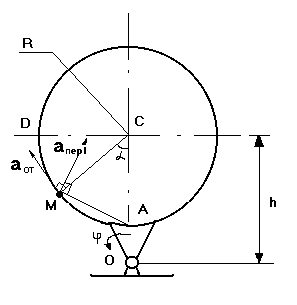
a, R=0.2 м

h=0.2 м

AM=S=

t1=0.5 c

vабс-? aабс-?

Решение:

Точка М совершает сложное движение, включающее в себя движение по окружности( относительное движение) и движение вместе с пластиной вокруг оси( переносное движение).

Рассмотрим относительное движение:

V=S’= (при t=0.5 Vотн= -0.75 м/с);S’’= . аотн= = =

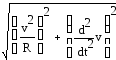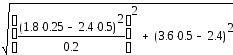= 2.876 м/. Vотн= -0.75 м/с.

Рассмотрим переносное движение:

w=’=4t-2(при t=0.5равно 0); ’’=4. Vпер=wR=(4t-2)R=(4(0.5)-2)0.2=0 м/с.aпер-N=0 м/. aпер-T= eOM= -0.9м/

акор=2|w|| Vотн|sin=0 м/.=2arcsin(AM/2R)= =-1.195 рад.

Исходя из полученных результатов, получаем:

Vабс= Vотн=-0.75 м/с.

aабс= = =3.031 м/.

Ответ: Vабс=-0.75 м/с; aабс=3.031 м/.

З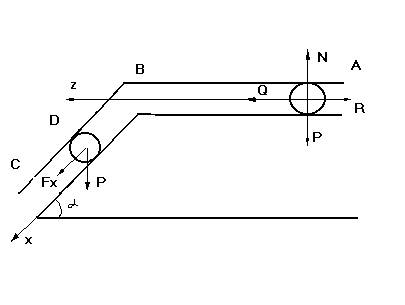адача 1.5.10.: Шар D, имеющий массу m, получив в точке А начальную скорость V0 ,движется по изогнутой трубе. Участки трубы- горизонтальный и наклонный. Угол наклона =30. На участке АВ на шар кроме силы тяжести ,действует постоянная сила Q, направленная вдоль трубы, и сила сопротивления R, зависящая от скорости шара. Не меняя скорости в точке В шар движется по участку ВС. На нем кроме силы тяжести действует переменная сила F, проекция которой на ось х задана. Считая шар материальной точкой, определить закон его движения на ВС, и определить на каком расстоянии от точки В будет находится шар через 1 с. после прохождения точки В.

Fx=-8sin(2wt);

=30

m=2 кг;

V0=0 м/c;

Q=2.4 H;

R=0.4V;

=0.4;

t1=5 c;

w=2 1/c;

f=0 H;

t2=1 c;

x(t)-? x2-? V2-?

Решение:

Рассмотрим участок АВ: mz’’=Fz; mz’’=Q-R=2.4-0.4z’;

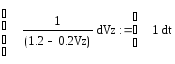уравнение движения: z’’=1.2-0.2z’, z’’=dVz/dt, z'=Vz dVz/dt=1.2-0.2Vz; dVz/(1.2-0.2Vz)=dt;

 ln(1.2-0.2Vz)=-0,2t+C1, где C1-определяется из начальных условий: при t=0

V=0:

ln(1.2-0.2(0))=C1 C1= ln(1.2). Подставляем в уравнение:

ln(1.2-0.2Vz)=-0,2t+ln(1.2)  ln((1.2-0.2Vz)/1.2)=-0.2t(1.2-0.2Vz)/1.2= 1-Vz/6= ;

для t1=5 c в точке В: Vz=6(1- )=3.8 м/c.

Рассмотрим участок ВС:

mx’’=Fx; mx’’=mgsin-ksin(2wt);

уравнение движения: x’’=5-4sin4t;x’’=dVx/dt dVx/dt=5-4sin4t; dVx=(5-4sin4t)dt;

Vx=5t+cos4t+C2, где C2- определяется по начальным условиям: при t=0 V=3.8 м/c. 3.8=1+C2 C2=2.8. Подставим в уравнение: Vx=5t+cos4t+2.8.

Закон движения по ВС: dx/dt=5t+cos4t+2.8dx=(5t+cos4t+2.8)dt;

x=5+(1/4)sin4t+2.8t+C3. По начальным условиям t=0, x=0C3=0.

Уравнение движения: x=5+(1/4)sin4t+2.8t. В момент времени t2=1 c: x2=5+(1/4)sin4+2.8=7.6 м.

V2=5+cos4+2.8=7.1 м/с.

Ответ: x=5+(1/4)sin4t+2.8t; x2=7.6 м; V2=7.1 м/с.

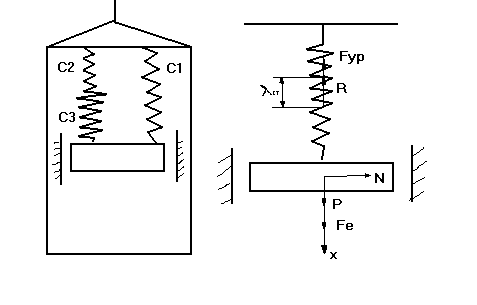
Задача 2.5.7.: Груз m закреплен на пружинной подвеске в лифте. Лифт движется вертикально по закону x1=0.5g .На груз действует сила сопротивления среды R=V. Найти закон движения груза по отношению к лифту.

x1=0.5g

m=0.4 кг;

ст=0.2 м;

a1=g;

a2= a3=0;

=8 Нс/м;

0=0;

V0=2 м/с;

x=f(t)-?

Решение:

Fe=ma=mx’’=m(0.5 g )’’=mg; ma=P-R-Fуп+Fe mx’’=Cст -x’-C(ст+x)+mg;

x’’=Cст/m-x’/m-C(ст+x)/m+g;

x’’+x’/m+Cx/m=g.С=mg/ст.x’’+x’/m+gx=g. Решение данного неодн. диф.уравнения представляет собой сумму общего и частного решения:

xобщ=; +2np+=0, где n=/2m, а =g; p12=-n+-=-0.5;-19.5 xобщ=C1+C2 .

x’=-0.5 C1-19.5C2 . C1 и C2 найдем из начальных условий: при t=0 x0=ст=0.2 м. V0=2 м/с.

C1 + C2=0.2; -0.5C1 –19.5 C2=2 C1=0.3; C2= -0.1.С учетом этого общее решение имеет вид:

xобщ=0.3-0.1C2 .

Частное решение находим в виде xчас=В; xчас’= xчас’’=0 xчас=g/g=1м.

Тогда уравнение движение тела в лифте имеет вид:

x= 0.3-0.1C2 +1(м).

Ответ: x=f(t)= 0.3-0.1C2 +1(м).