
- •Министерство российской федерации
- •Часть 1. Общая теория статистики
- •Раздел 1. Введение в статистику
- •Принципами официального статистического учета и системы государственной статистики являются:
- •Основные задачи статистики мчс
- •Раздел 2. Сбор и обработка статистической информации
- •Средняя хронологическая
- •Средняя гармоническая
- •Структурные средние
- •Расчет медианы интервального ряда
- •Свойство медианы
- •Раздел 3. Статистические распределения и анализ вариационных рядов
- •6. Из величины, выражающей дисперсию, извлекают квадратный корень:
- •Свойства дисперсии:
- •Правило сложения дисперсий
- •Нормальное распределение
- •Распределение Пуассона
- •Раздел 4. Методы изучения статистических связей
- •Раздел 5. Исследование рядов динамики
- •Прогнозирование на основе рядов динамики и регрессионных моделей
- •Особенности прогнозирование на основе рядов динамики
- •Прогнозирование на основе регрессионных моделей
- •Часть 2. Социально-экономическая статистика
- •Раздел 6. Основные направления статистического изучения населения
- •Раздел 7. СтатистиКа социально-трудовых отношений
- •- Коэффициент использования табельного фонда времени:
- •- Коэффициент использования максимально возможного фонда времени:
- •- Средняя продолжительность рабочего дня в часах:
- •- Коэффициент использования полной продолжительности рабочего дня:
- •Раздел 8. Характеристика национального богатства
- •I. Основные показатели движения основных фондов:
- •II. Основные показатели состояния основных фондов:
- •III. Основные показатели использования основных фондов:
- •Раздел 9. Статистический анализ основных макроэкономических показателей
- •Основные макроэкономические показатели снс:
- •Баланс активов и пассивов на начало / конец периода
- •Денежные доходы населения:
- •Денежные расходы и сбережения:
- •Раздел 10. Статистическое исследование благосотояния населения
- •Алгоритм расчета ипц:
- •Раздел 11. Организация статистического учета в мчс России
- •Количественные показатели чрезвычайных ситуаций, происшедших в минувшем году
- •Сведения о массовых инфекционных заболеваниях и отравлениях людей
- •Сравнительная характеристика техногенных чрезвычайных ситуаций, происшедших на территории (наименование субъекта рф) в_______гг.
- •Сравнительная характеристика чрезвычайных ситуаций природного характера, происшедших на территории (наименование субъекта рф) в_______гг.
- •Сведения о массовых инфекционных, паразитарных и зоонозных заболеваниях животных и птицы
- •Сведения о распространении наиболее опасных болезней и вредителей сельскохозяйственных растений
- •Сведения о распространении наиболее опасных болезней и вредителей леса
- •Показатели состояния поисково-спасательных формирований на водных объектах (наименование субъекта Российской Федерации)
- •Состояние профилактики массовых инфекционных заболеваний сельскохозяйственных животных и птицы
- •Сведения о полной или частичной остановке потенциально опасных объектов
- •Состояние предупреждения болезней и вредителей сельскохозяйственных растений и леса
- •Сведения о проведении государственного надзора и контроля в области защиты населения и территорий от чрезвычайных ситуаций
- •Число пострадавших в субъектах Российской Федерации за 200_ год от чс
- •Сведения о применения сил и средств при ликвидации чс
- •Оснащенность потенциально опасных объектов системами предотвращения аварий
- •Глоссарий
- •Литература
Свойства дисперсии:
1. Дисперсия постоянной величины равна нулю.
2. Дисперсия не меняется, если все варианты увеличить или уменьшить на одно и то же число.
3. Постоянный
множитель выносится за знак дисперсии
возведенным в квадрат. Другими словами,
если все варианты умножить на какое-либо
число
![]() ,
то дисперсия увеличиться в
,
то дисперсия увеличиться в![]() раз.
раз.
4. Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и этой произвольной величиной - это свойство носит название свойства минимальности дисперсии от средней.
Использование свойств дисперсии позволяет упрощать ее расчеты, особенно в тех случаях, когда вариационный ряд составляет арифметическую прогрессию или имеет равные интервалы.
Правило сложения дисперсий
Если совокупность
состоит из нескольких частей, то можно
определить в пределах каждой не только
среднюю величину, но и дисперсию
![]() (частную дисперсию). Обозначив через
(частную дисперсию). Обозначив через![]() отклонение простой средней от общей,
получим:
отклонение простой средней от общей,
получим:

Правило сложения дисперсий означает, что общая дисперсия складывается из двух слагаемых, одно из которых измеряет вариацию внутри частей совокупности, а второе — различия (вариацию) между этими частями (представленными средними). Именно поэтому правило сложения дисперсий находит широкое применение в анализе взаимосвязей и зависимостей.
Наглядно представить статистические данные позволяет графический метод, заключающийся в изображении показателей при помощи геометрических фигур и т.д. Передаваемая графически информация воспринимается значительно лучше, чем текстовая запись цифровых данных.
Поле графика — это пространство, в котором располагается графический образ.

Рис. 3.2. Полигон распределения семей по числу их членов
Шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа.
Масштаб — мера перевода числовой величины в графическую. Масштаб графика выражается линейной мерой, т.е. числом миллиметров в отрезке, которому должна соответствовать единица статистического показателя.
В большинстве случаев в статистических графиках применяется система декартовых координат. Графический образ зависит от используемых геометрических знаков и может быть точечным, круговым, столбиковым и др.
Диаграмма — наиболее распространенная форма графических изображений.
Диаграмма столбиковая изображает статистические величины в форме удлиненных прямоугольников (столбиков). Столбиковая диаграмма — диаграмма одномерного измерения, поэтому все столбики по ширине должны быть одинаковыми, так как величина показателя характеризуется высотой столбика, и размещаться на горизонтальной прямой на равном расстоянии друг от друга. Пример столбиковой диаграммы, отражающей динамику застройки одного из районов г. Москва (Северное Бутово) приведен на рис.3.3.

Рис.3.3. Динамика застройки одного из районов г. Москва (Северное Бутово) за 2007-2010 гг. [21]
Разновидностью полосовой диаграммы является скользящая диаграмма. В скользящей полосовой диаграмме направленность полос определяется не их нулевыми точками, а условными значениями, по которым полосы смещаются друг против друга вправо и влево. Полосовой скользящей диаграммой можно графически изобразить данные демографической статистики о вероятной продолжительности жизни людей в зависимости от пола и возраста.
Широкое применение имеют линейные диаграммы, которые иначе называются статистическими кривыми, и отражают изменение явления во времени.
При непрерывной вариации признака строятся интервальные вариационные ряды, графическим изображением которых является гистограмма. Для ее построения по оси абсцисс в соответствии с принятым масштабом откладывают границы интервалов признака. Эти интервалы являются основаниями прямоугольников, площади которых равны произведению величины интервалов на их частоты или частости.
В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята). Для ее построения следует рассчитать накопленные частоты или частости, на оси абсцисс откладываются значения варьирующего признака, а на оси ординат помещаются накопленные частоты или частости. Например, имеются следующие данные о распределении семей по числу детей (цифры условные):
Таблица 3.1
Данные о распределении семей по числу детей (цифры условные)
-
Число детей в семье (х)
Численность семей в процентах к итогу (частость – f),%
Накопленная частость (s),%
0
1
2
3
4
25
45
18
10
2
25
70
88
98
100

Рис. 3.4. Кумулята распределения семей по числу детей, соответствующая данным табл.3.1.
Секторная диаграмма применяется для иллюстрации структуры изучаемой совокупности. Секторные диаграммы строятся по следующему принципу: вся величина явления принимается за 100%, затем считаются доли отдельных частей в процентах. Круг разбивается на секторы пропорционально частям изображаемого целого, т.е. на 1% приходится 3,6 градуса. Чтобы получить центральные углы секторов, отображающие доли частей целого, следует их процентное выражение умножить на 3,6 градуса Например, на рис. 3.5. показан характер возникновения ЧС в 2007 г.[19] (в 2009 г. произошла 270 ЧС техногенного характера, количество ЧС природного характера составило 133, произошла 21 биолого-социальная ЧС).

Рис. 3.5. Характер возникновения ЧС в 2007 г.[19]
Для одновременного изображения трех величин, связанных между собой таким образом, что одна величина является произведением двух других, применяются диаграммы, называемые знак Варзара (по имени русского статистика В.Е. Варзара) и представляет собой прямоугольник, у которого один сомножитель принят за основание, другой – за высоту, а вся площадь равна их произведению (рис.3.6). Например, имеются следующие данные, приведенные в табл. 3.2. (цифры условные):
Таблица 3.2
|
Показатели |
Посевная площадь, млн. га |
Урожайность, ц/га |
Валовой сбор, млн. ц |
|
Пшеница озимая
|
14,9
|
17,9
|
248,8
|
|
Пшеница яровая |
39,4 |
18,2 |
717,1 |

Рис. 3.6. Валовой сбор озимой и яровой пшеницы
Графический метод в статистике является продолжением и дополнением табличного метода. График позволяет сравнительно легко обнаружить на глаз ошибки расчетов, которые в табличной форме не были так заметны. Незамеченными при чтении таблиц могут оставаться не только ошибки, но какие-то тенденции. Все это обнаруживается на графике. Статистические графики отражают целостную картину изучаемого явления, его обобщенное представление.
При графическом изображении статистических данных становится более выразительной сравнительная характеристика изучаемых показателей, отчетливее проявляется тенденция развития изучаемого явления, лучше видны основные взаимосвязи.
Анализ вариационных рядов
Одной из важных задач анализа рядов распределения является выявление закономерности распределения, определения ее характера и количественного выражения. Эта задача решается при помощи показателей, характеризующих форму, тип распределения.
Кроме рассмотренных выше важной характеристикой рядов распределения являются также моменты распределений.
Моментом
распределения
![]() называется средняя арифметическая из
отклонений значений признака
называется средняя арифметическая из
отклонений значений признака
![]() от некоторой постоянной величины
от некоторой постоянной величины
![]() в степени
в степени
![]() .
.
Порядок момента
определяется величиной
![]() .
Эмпирический момент
.
Эмпирический момент
![]() -го
порядка определяется по формуле
-го
порядка определяется по формуле

В зависимости от
постоянной величины
![]() различают:
различают:
- начальные,
- центральные и
- условные моменты.
Если
![]() ,
то моменты называются начальными и
определяются по формуле
,
то моменты называются начальными и
определяются по формуле
 ;
;
В этом случае при
![]() получаем начальный момент нулевого
порядка, который равен
получаем начальный момент нулевого
порядка, который равен
 .
.
При
![]() получаем начальный момент первого
порядка, который равен:
получаем начальный момент первого
порядка, который равен:
 ,
,
при
![]() - начальный момент второго порядка,
равный
- начальный момент второго порядка,
равный
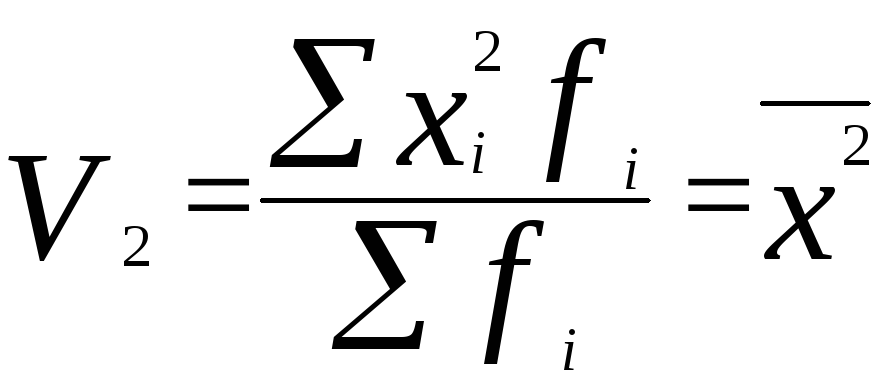 ,
,
и т.д.
Начальные моменты
используются, в частности, при расчете
дисперсии:
![]() .
.
Если постоянная
величина
![]() ,
то получим центральные моменты, которые
определяются по формуле
,
то получим центральные моменты, которые
определяются по формуле
 .
.
В этом случае при
![]() получим центральный момент нулевого
порядка, который равен
получим центральный момент нулевого
порядка, который равен
 ,
,
при
![]() - центральный момент первого порядка,
равный:
- центральный момент первого порядка,
равный:
 ,
,
при
![]() - центральный момент второго порядка,
равный:
- центральный момент второго порядка,
равный:
 ; и
т.д.
; и
т.д.
В формулах для
вычисления условных моментов
![]() представляет
собой определенное значение.
представляет
собой определенное значение.
Анализ вариационных рядов предполагает выявление закономерностей распределения, определение и построение некой теоретической (вероятностной) формы распределения. Графическое изображение эмпирического вариационного ряда принимает вид плавной кривой, именуемой кривой распределения. Характер распределения лучше всего проявляется при большом числе наблюдений и малых интервалах.
Кривая распределения является обобщенной характеристикой особенностей формы распределения и выражает закономерность распределения единиц совокупности по величине варьирующего признака.
Различают кривые распределения эмпирические и теоретические.
Эмпирическая кривая — кривая распределения, полученная по данным наблюдения, которая отражает как общие, так и случайные условия, определяющие распределение.
Теоретическая кривая распределения — кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения.
Анализируя частоты в эмпирическом распределении, можно описать его с помощью математической модели — закона распределения, установить по исходным данным параметры теоретической кривой и проверить правильность выдвинутой гипотезы о типе распределения данного ряда. Нахождение функции кривой распределения называется моделированием.
При исследовании закономерностей распределения очень важно выдвинуть верную гипотезу о типе кривой распределения, так как, если кривая описана математически (с помощью уравнения) верно, она более точно отражает закономерности данного распределения и может быть использована в различных практических расчетах и прогнозах, в этом случае можно сформулировать рекомендации для принятия практических решений.
Для аппроксимации (выравнивания) эмпирических кривых распределения и сопоставления их с теоретическими в практике статистического исследования часто используют различные распределения: нормальное, логарифмически нормальное, биномиальное, Пуассона, Шарлье и др.
Каждое распределение имеет свою специфику и область применения. Далее будут рассмотрены только нормальное распределение и распределение Пуассона.
