7.2. Горение в замкнутом объеме.

При горении газов в открытой трубе и в потоке продукты реакции свободно расширяются, давление остается практически постоянным. Сжигание в замкнутом сосуде связано с ростом давления. Это имеет большое значение для решения задач взрывобезопасности. Повышение давления при сгорании в замкнутых аппаратах, а также в помещениях, может приводить к разрушениям и авариям.

При горении без тепловых потерь (адиабатическом горении) в замкну­-том объеме в результате повышения температуры с Т_о до температуры горе­-ния Т_г и изменения числа грамм-молекул при реакции давление возрастает с Р_о до Р_г:

(7.8)

где: m, n – число молей веществ до и после взрыва стехиометрическо-

го состава смеси.

Однако наибольшее давление развивается не для стехиометрических смесей, хотя они обладают наибольшей теплотой сгорания и создают макси­-мальную Т_г, а смеси, обогащенные горючим веществом, которые имеют мак­-симальную скорость горения. При дефлаграционном горении давление дос­-тигает 7-10 атм., при детонации – намного выше.

Характерной особенностью процесса сгорания в замкнутом объеме является неравномерность распределения температуры продуктов реакции непосредственно после сгорания. Первоначально сгорающая часть горючей смеси, находящаяся в центре сосуда, реагирует при начальном давлении р_о; последний слой, сгорающий у стенки, реагирует при конечном давлении р.

Нагревание каждого слоя газа протекает в две стадии: при химическом превращении и адиабатическом сжатии. Хотя во всех точках объема состав продуктов сгорания и давление одинаковы, конечная температура существенно зависит от последовательности обоих нагревающих процессов. При адиабатическом сжатии от давления р_о до давления р рост температуры от Т_о до Т определяется уравнением Пуассона

, (7.9)

где:  = с_р/с_v.

Конечная температура продуктов сгорания будет выше в том случае, ес-ли газ сначала нагревается при химическом превращении, а затем его темпе- ратура возрастает при сжатии по уравнению (7.9), чем в случае обратной пос-ледовательности обоих процессов.

7.3. Движение газов при горении.

Расширение газов в пламени (по закону Гей-Люссака) приводит к тому, что горение всегда сопровождается движением газов. Обозначим через ρ_г – плотность исходной среды, ρ_пр – плотность продуктов горения, их скорость по отношению к неподвижному фронту пламени равна u_пр. На каждый квад-ратный сантиметр поверхности фронта поток приносит ежесекундно u_н см³ горючей смеси, её масса равна u_н*ρ_г соответственно от этого участка пламени отводится в 1 сек u_пр см³ продуктов реакции с массой u_пр*ρ_пр. Поскольку мас-сы сгорающей смеси и продуктов реакции равны, то

u_н*ρ_г = u_пр*ρ_пр (7.10)

Уравнение (7.10) выражает закон сохранения массы при горении.

Величина u_пр превосходит нормальную скорость пламени во столько раз, во сколько плотность исходной среды больше плотности продуктов сгорания. Увеличение скорости газового потока при сгорании является след-ствием расширения газов.

Абсолютная температура при сгорании повышается в 5–10 раз. Если горение происходит при постоянном давлении, газ расширяется в _о/р_пр раз. Рассмотрим горение стационарного фронта пламени в открытой трубе, изоб-раженной на рисунке 28.

ρ_ПР

Р

ω

ис. 28. Схема пояснения закона площадей:S – сечение трубы, F – поверхность фронта пламени, ω - скорость исходной горючей смеси, Т₀ ,- тем­пература и плотность исходной смеси,U_H – нормальная скорость горения, U_ПЛ – скорость рас­-пространения пламени, U_ПР – скорость продуктов горения, Т_ПР, - температура и плотность про-дук­тов горения.

Так как пламя располагается неподвижно, ω = U_ПР. Тогда, например, на 1 см² поверхности фронта пламени F поток приносит ω см³/с горючей смеси. Её масса равна ω. Соответственно от этого участка отводитсяU_ПР см³/с про­дуктов сгорания с массою U_ПР. Тогда по закону сохранения масс (уравне­ние 7.10) приω = U_ПЛ:

(7.11)

Таким образом, объемная скорость продуктов сгорания превышает ско­-рость горения во столько раз, во сколько плотность исходной среды больше плотности продуктов горения.

С другой стороны, если на 1 см² поверхности фронта пламени сгорает U_Н см³/с смеси, то на всей площади F сгорает U_Н*F см³/с. В то же время объ-ем сгорающего газа равен объемной скорости газового потока ω*S см³/с. То-гда U_H*F = ω*S, или ω = U_H*F / S.

При равенстве ω =U_ПЛ:

U_ПЛ = U_H*F / S. (7.12)

Получаем закон площадей: скорость распространения пламени в трубе будет во столько раз больше нормальной, во сколько поверхность пламени превосходит поперечное сечение трубы.

Если рассматривать неподвижную горючую смесь, то при распростра­-нении фронта пламени резко нагретые газы не успевают расширяться, и в зо-не горения резко повышается давление, которое «распирает» и выталки­вает газы в обе стороны от пламени, причем выталкиваются не только про­дукты горения, но и возникает движение исходной смеси впереди фронта пламени, как на рисунке 29:

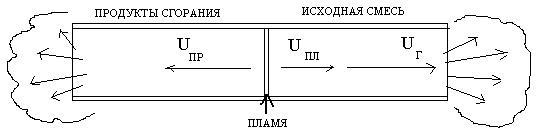
Рис. 29.

Скорость газов возрастает по мере сгорания исходной смеси и соответ­-ственно, давления газов. При этом с одного конца трубы выбрасываются сжа-тые раскаленные сгоревшие газы, а с другого выталкивается сжатая исходная смесь, которая взрывообразно воспламеняется от выброшенного пламени в атмосфере помещения с последующей ударной волной, пожаром и разруше­-нием.