лекции студентов(есть опечатки и замечания) / 1семестр_ответы / экз.ответы 15-24 (1 семестр)

Билет 15

Понятие о линейном векторном пространстве. Понятие n-мерного вектора. Линейная зависимость и независимость векторов.

Билет 16

Базис линейного пространства. Координаты вектора в базисе. Ортонормированный базис. Прямоугольная (декартова) система координат.

n- мерный вектор. Будем называть n-мерным вектором упорядоченную последовательность чисел а₁, а₂, … , а_n. При этом записывают =( а₁, а₂, … , а_n ).

Линейно-независимые вектора. По определению система линейно - независима, если из векторного равенства λ₁а₁ + λ₂а₂ + … + λ_kа_k = 0, где λ₁, λ₂, … , λ_k – числа. Следует, что λ₁= λ₂= … =λ_k=0.

Линейное пространство – (то же, что векторное пространство) – математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число – скаляр.

Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:

1. система линейно независима.

2. Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов ):

Пусть L = Rⁿ

Для каждого вектора существуют числа такие что

Числа называются координатами вектора в базисе () (определяются однозначно), X = (x) - координатный столбец вектора в этом базисе.

Ортонормированный базис

Ортогональные векторы – такие векторы 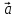и , скалярное произведение которых = 0.

*=0

Базис называется ортонормированным, если его векторы попарно ортогональны и длины их равны единице.

Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.

Билет 17

Евклидово пространство. Норма вектора. Множество. Мера плоского множества.

Скалярное произведение векторов – число, равное произведению модулей этих векторов на косинус угла между ними.

Векторное пространство, в котором определено скалярное произведение, называется евклидовым пространством.

Длина (норма) вектора:

Длиной вектора x в евклидовом пространстве E мы будем называть величину

= +

длина вектора определяется по формуле:

= + .

Мера множества:

Мера множества в R является его длина. Мерой множества в трехмерном пространстве является его объем. Мерой множества на плоскости является его площадь.

Множество называется замкнутым относительно некоторой операции, если результат применения этой операции к любым элементам данного множества является элементом этого же множества.

Пример. Множество натуральных чисел N замкнуто относительно операций сложения и умножения, т.к. сумма и произведение двух натуральных чисел также натуральное число.

Множество Z целых чисел замкнуто относительно операций сложения, вычитания и умножения.

Множество Q рациональных чисел замкнуто относительно операций сложения, вычитания, умножения и деления.

Множество R действительных чисел замкнуто относительно операций сложения, вычитания, умножения, деления и извлечения корня.

Билет 18

Евклидово пространство. Собственные значения и векторы матрицы.

Скалярное произведение векторов – число, равное произведению модулей этих векторов на косинус угла между ними.

Векторное пространство, в котором определено скалярное произведение, называется евклидовым пространством.

18. Собственные векторы и собственные значения

Пусть A — это квадратная матрица. Вектор называется собственным вектором матрицы A, если A = λ, где число λ называется собственным значением матрицы A. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если 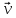— собственный вектор, то и α — тоже собственный вектор.

Собственные значения

У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению det(A − λЕ) = 0, являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

Собственные векторы

У матрицы A, размерностью (N×N) не может быть больше, чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v_n нужно решить систему однородных уравнений

(A – λ _nE) v_n = 0.

Билет 19* Линейная модель обмена Леонтьева.

Билет 19

Квадратичные формы. Приведение к каноническому виду.

Квадратичной формой действительных переменных х₁, х₂,…,х_n называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Примеры квадратичных форм:

(n = 2),

(n = 3).

Приведение квадратичной формы к каноническому виду.

Каноническим видом квадратичной формы называется следующий вид:

Покажем, что в базисе из собственных векторов квадратичная форма примет канонический вид. Пусть

- нормированные собственные векторы, соответствующие собственным числам λ₁,λ₂,λ₃ матрицы в ортонормированном базисе . Тогда матрицей перехода от старого базиса к новому будет матрица

В новом базисе матрица А примет диагональный вид (по свойству собственных векторов). Таким образом, преобразовав координаты по формулам:

получим в новом базисе канонический вид квадратичной формы с коэффициентами, равными собственным числам λ₁, λ₂, λ₃:

Билет 20

Полярная система координат и прямоугольная (декартова).

Определение полярной системы координат

Из элементарной геометрии известно, что единственная плоскость в пространстве может быть задана: двумя прямыми (пересекающимися или параллельными), прямой и точкой или тремя точками.

Плоскость, образованная двумя пересекающимися, взаимно перпендикулярными прямыми представляет собой декартову прямоугольную систему координат, началом которой служит точка пересечения прямых.

Положение некоторой точки A на этой плоскости определяется числами x и y, где x - расстояние от т. A до оси ординат (вертикальной прямой), y - расстояние от т. A до оси абсцисс (горизонтальной прямой). Это записывается в виде: A (x, y).

До сих пор изучалась и пользовалась система координат плоскости, образованной двумя пересекающимися прямыми. Попробуем определить положение некоторой точки B в плоскости, образованной прямой и самой точкой B. Отметим на некоторой физической плоскости (например, на листе бумаги) точку B. Из некоторой точки O на плоскости, которую будем называть полюсом, проведем луч в направлении слева направо и будем называть его полярной осью. Соединим полюс с точкой B и будем называть этот отрезок полярным радиусом. Отметим угол между полярной осью и полярным радиусом Тогда местоположение точки B на плоскости будет определятся полярным радиусом - r, выражающем длину отрезка в заданном масштабе и полярным углом - . За положительное направление полярного угла a будем считать направление против часовой стрелки, а полярный радиус будем считать всегда неотрицательным. Это записывается в виде : B (r, ).

Определение. Полярной системой координат называется такая система, в которой местоположение точки B задается в плоскости, образованной некоторой прямой и точкой B. Началом системы координат служит точка O на прямой, называемая полюсом, а координатами точки B являются: расстояние от полюса до точки B, называемое полярным радиусом и угол , образованный полярной осью и полярным радиусом.

Всякой точке этой системы будет соответствовать единственная пара полярных координат и наоборот: по заданной паре полярных координат определяется местоположение точки в плоскости.

Переход от полярных координат к декартовым и обратно.

Если полярную и декартову прямоугольную системы совместить так, чтобы начала их координат совпадали, а полярная ось совпадала с положительным направлением оси абсцисс прямоугольной системы, то независимо от расположения точки B на плоскости получим формулы перехода от полярных координат r, a к декартовым x, y:

x = r cos ; y = r sin

и от декартовых к полярным:

Билет 21

Определение скалярного произведения двух векторов. Формула для вычисления скалярного произведения векторов в координатной форме. Свойства скалярного произведения.

Билет 22

Понятие правой тройки векторов. Определение векторного произведения двух векторов. Формула для вычисления векторного произведения векторов в координатной форме. Свойства векторного произведения. Геометрический смысл модуля векторного произведения (на примере 6 из т.р.2)

Правая тройка векторов

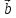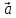Тройка некомпланарных векторов , , называется правой (левой), если после приведения к общему началу нулевой вектор располагается по ту сторону от плоскости, определяемой векторами и , откуда кратчайший поворот от к кажется совершающимся против часовой стрелки (по часовой стрелке).

Векторное произведение векторов.

Вектор называется векторным произведением векторов и , если:

1)|| = ||||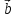sin, где – угол между и .

2), .

3)Тройка векторов , , 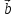является правой.

Обозначения векторного произведения: = [,], = ×

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов и есть вектор , где - координатные векторы.

Свойства векторного произведения.

1) × = - × .

Доказательство. Вектор - удовлетворяет первым двум условиям определения векторного произведения и образует с векторами и правую тройку векторов.

2) × = ║ .

Доказательство. Из первого пункта определения следует, что модуль векторного произведения ненулевых векторов равен нулю только при sin = 0, что соответствует коллинеарности векторов и .

3)Модуль векторного произведения | × | равняется площади S параллелограмма, построенного на приведенных к общему началу векторах векторов и . Доказательство следует из первого пункта определения.

Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах, как на сторонах.

Билет 23

Определение смешанного произведения трех векторов. Выражение смешанного произведения через координаты. Свойства смешанного произведения. Геометрический смысл модуля смешанного произведения (на примере 7 из т.р.2)

модуль смешанного произведения векторов ,, 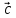равен произведению длин этих векторов, т.е.| |=||||||.

Билет 24

Уравнение линии на плоскости. Точка пересечения двух линий.

Единственная общая точка двух пересекающихся прямых есть точка пересечения этих прямых.

Нахождение координат точки пересечения двух прямых на плоскости

Прежде чем находить координаты точки пересечения двух прямых на плоскости по их известным уравнениям, рассмотрим вспомогательную задачу.

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и заданы две пересекающиеся прямые l₁ и l₂. Будем считать, что прямой l₁ соответствует общее уравнение прямой вида , а прямой l₂ – вида . Пусть – некоторая точка плоскости, и требуется выяснить, является ли точка М₀ точкой пересечения заданных прямых.

Решим поставленную задачу.

Если M₀ является точкой пересечения прямых l₁ и l₂, то по определению она принадлежит и прямой l₁ и прямой l₂, то есть, ее координаты должны удовлетворять одновременно и уравнению и уравнению . Следовательно, нам нужно подставить координаты точки М₀ в уравнения заданных прямых и посмотреть, получаются ли при этом два верных равенства. Если координаты точки М₀ удовлетворяют обоим уравнениям и , то – точка пересечения прямых a и b, в противном случае М₀ не является точкой пересечения прямых.

Нахождение координат точки пересечения двух прямых в пространстве.

Координаты точки пересечения двух прямых в трехмерном пространстве находятся аналогично.

Пусть пересекающиеся прямые l₁ и l₂ заданы в прямоугольной системе координат Oxyz уравнениями двух пересекающихся плоскостей, то есть, прямая l₁ определяется системой вида , а прямая l₂ - . Пусть М₀ – точка пересечения прямых l₁ и l₂. Тогда точка М₀ по определению принадлежит и прямой l₁ и прямой l₂, следовательно, ее координаты удовлетворяют уравнениям обеих прямых. Таким образом, координаты точки пересечения прямых l₁ и l₂ представляют собой решение системы линейных уравнений вида . Здесь нам умение решать системы линейных уравнений, в которых число уравнений не совпадает с числом неизвестных переменных.