37. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых в пространстве.

Под углом между этими прямыми понимают угол между их направляющими векторами S₁=(m₁;n₁;p₁) иS₂=(m₂;n₂;p₂). Тогда, по формуле для косинуса угла между векторами, получаемили.

Пример: Заданы прямые l₁:иl₂: ; S₁=(m₁;n₁;p₁)=(1;-0,5;1) иS₂=(m₂;n₂;p₂)=(1;-9;-6).

Подставляем наши значения в формулу: .

Для нахождения острого угла между прямыми числитель правой части формулы следует взять по модулю.

Если прямые перпендикулярны, то в этом и только в этом случае имеем 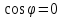. Следовательно, числитель дроби равен нулю, т. е., так как | S₁|и | S₂|.

Если прямые параллельны, то параллельны их направляющие векторы. Следовательно, координаты этих векторов пропорциональны, т. е. .

38.Угол между прямой на плоскости и плоскостью в пространстве. Условия параллельности и перпендикулярности их в пространстве.

Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и её проекцией на плоскость. Обозначим через 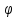угол между плоскостьюQи прямойl, а через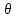- угол между векторами=(A;B;C) и. Тогда. При этом: если, то; если, то.

.

Пример: Даны плоскость Q: x+3y+5z-42=0 и прямаяL: .

.

Острый угол между плоскостью и прямой можно найти, взяв в формуле модуль правой части.

Если прямая l параллельна плоскости Q, то векторыи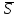перпендикулярны, а потому, т. е.–условие параллельности прямой и плоскости.

Если прямая L перпендикулярна плоскости Q, то векторыипараллельны. Поэтому равенства–условие перпендикулярности прямой и плоскости.

Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости.

Чтобы найти точку пересечения прямой и плоскости нужно решить систему, состоящую из уравнений прямой и плоскости. Проще всего это сделать, записав уравнения прямой в параметрическом виде: l:.

Подставляя эти выражения для x, yи zв уравнение плоскости, получаем уравнениеили;, и приведя подобные, мы получаем значение, но при условии, что прямая не параллельна плоскости, т. е..

Пример: Требуется найти точку пересечения прямой l: с плоскостьюQ: x+3y+5z-42=0.

Подставляя найденное значение параметра в параметрические уравнения прямой, найдем координаты точки пересечения прямой с плоскостью:, т. е. точкаО(4;1;7) – точка пересечения прямойlс плоскостьюQ.

Рассмотрим случай, когда :

А) если , то прямая параллельна плоскости и пересекать ее не будет, т. е. уравнениерешения не имеет.

Б) если , то уравнениюудовлетворяет любое значение, любая точка прямой является точкой пересечения прямой и плоскости. Следовательно, прямая лежит на плоскости.

Таким образом, одновременное выполнение равенств являетсяусловием принадлежности прямой плоскости.