6.4. Эффективное сечение рассеяния частиц с электростатическим взаимодействием. Формула резерфорда

Применим полученные формулы к одному из важных физических примеров - рассеянию электрически заряженных частиц. Положив в (3.6) получим

,

здесь - приведенная масса, - относительная скорость частиц до рассеяния, а является положительным корнем уравнения

.

Вычисляя интеграл, для угла рассеяния в ц-системе получаем

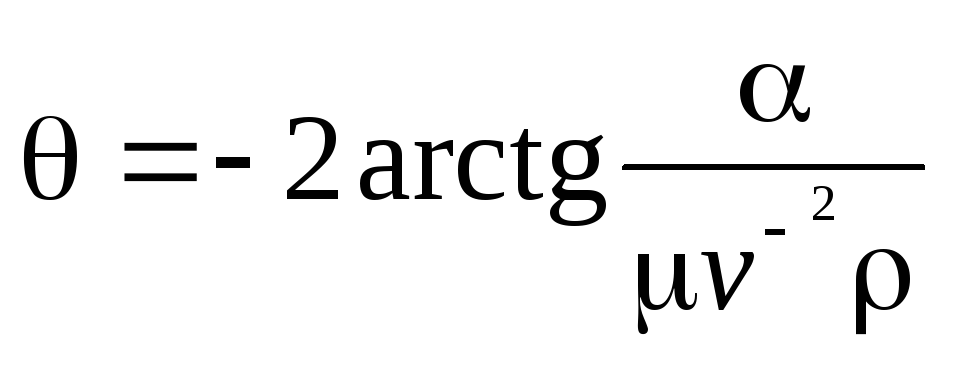. (16.6)

В случае сил притяжения () угол рассеяния отрицательный, а если взаимодействие носит характер отталкивания (), то . Обращая формулу (16.6), получим

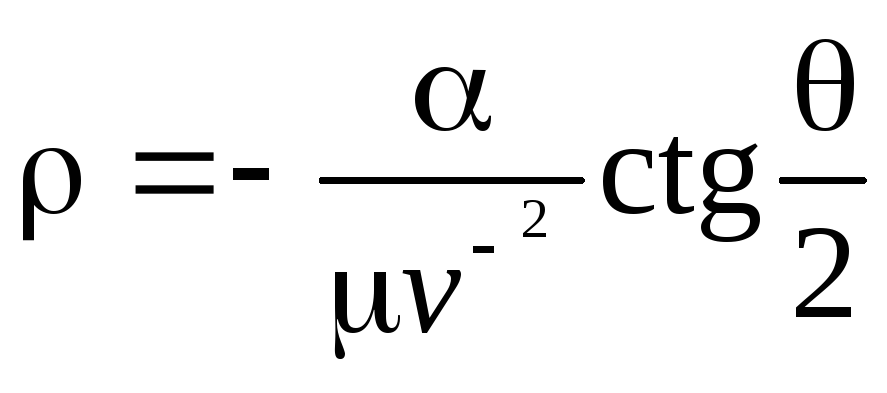. (17.6)

Дифференцируя это выражение по и подставляя результат в (13.6) или (15.6), находим

,

или

. (18.6)

Это формула Резерфорда. Мы видим, что эффективное сечение рассеяния не зависит от знака , так что формулой Резерфорда описывается как случай притяжения, так и случай отталкивания.

В ряде задач теории рассеяния можно ввести понятие полного эффективного сечения рассеяния как величины, равной отношению числа частиц, рассеиваемых за единицу времени под всеми углами , к плотности потока падающих частиц:

. (19.6)

Из этой формулы следует, что если радиус действия сил ограничен, т. е. потенциальная энергия взаимодействия имеет вид при при , то будет равно площади круга радиуса :

. (20.6)

Если ввести полное сечение для процесса рассеяния заряженных частиц, то нетрудно показать, что оно обращается в бесконечность. Говорят в этом случае, что полное сечение расходится. Эта расходимость связана с существованием взаимодействия между частицами при сколь угодно больших прицельных расстояниях, т. е. фактически она возникает из-за бесконечно большого «радиуса действия» кулоновских сил. Дело в том, что при вычислении мы учитываем вклад всех рассеянных частиц, включая частицы с прицельным расстоянием и соответственно . Легко видеть, что при расходится и , так как

.

Следует отметить, что эта расходимость присутствует и в формулах , полученных методами квантовой теории. Ее причина также связана с дальнодействующим характером кулоновских сил.

6.5. Захват частиц. Полное сечение захвата

Рассмотрим графики эффективных энергий, представленные на рис. 7.6, и поставим вопрос: в чем они существенно различны? Ответ, очевидно, заключается в следующем: на рис. 7.6,а изображен случай, когда для всех (любых) In-состояний существуют Out-состояния, в то время как в случае рис. 7.6,б некоторые In-состояния не имеют Out-состояний. Легко видеть, что частицы, находящиеся при в In-coстояниях с энергиями будут падать на центр поля.

Подобно тому как это было сделано для задачи рассеяния, здесь также можно ввести некоторую физическую величину, которой удобно характеризовать процесс. Если речь идет о взаимодействии пучков частиц, то отсутствие Out-состояний в такой задаче, очевидно, означает, что обе частицы при совершают движение в ограниченной области пространства. В таком случае говорят о захвате частиц. Процесс характеризуют полным сечением захвата, которое определяют как отношение числа частиц данного пучка, захваченных за единицу времени, к плотности потока этого пучка до рассеяния. Как и ранее, задача захвата двух частиц приводится к задаче о движении -точки.

Условия падения на центр поля -точки запишем, используя параметры задачи рассеяния и :

(21.6)

и далее

. (22.6)

Этой формулой и определяются условия падения на центр поля.

Поставим вопрос: при каких значениях неравенство удовлетворяется? Очевидно, если , т. е. если взаимодействие носит характер отталкивания, неравенство не удовлетворяется ни при каких значениях . В случае же притяжения, по крайней мере, если силы притяжения быстро убывают при , падение становится возможным хотя бы для некоторых : . Значит, в этом случае при происходит захват частиц. Полное сечение захвата, согласно данному выше определению, вычисляется по формуле

. (23.6)

Рис. 8.6

Пример. Найти полное сечение захвата частиц с энергией в поле

Эффективная потенциальная энергия , где Падение на центр поля возможно, только если , т. е. при . При этом должно выполняться неравенство где (рис. 8.6). Найдем . . Отсюда и .

Из условия получим

и . Значит, . Так как величина должна быть положительной, то окончательно найдем

;

.