Глава 6 упругое рассеяние частиц
6.1. Общая постановка задачи
В теоретической механике в рамках задачи двух тел решают в основном две задачи: задачу определения значений энергии системы, траекторий частиц, движущихся в ограниченной области пространства, и задачу рассеяния частиц, которая включает в себя исследование упругого рассеяния. Рассеяние двух частиц называют упругим, если в этом процессе не происходит изменения внутреннего состояния взаимодействующих частиц.
Постановка
задачи рассеяния состоит в следующем.
Прежде всего удобно считать начальным
моментом времени 
.
При этом предполагается, что при 
частицы не
взаимодействуют между собой (являются
свободными), так как они бесконечно
далеки друг от друга и вследствие этого
энергия их взаимодействия, являющаяся
убывающей функцией расстояния между
ними, равна нулю. Далее частицы
взаимодействуют между собой, однако
при 
они расходятся
на большое расстояние и их энергия
взаимодействия снова обращается в нуль.
Задача
заключается в том, чтобы определить
механическое состояние системы частиц
при 
,
задав их состояние при 
.
В квантовой механике состояния частиц
при 
называют In-состояниями,
а при 
- Out-состояниями. Удобно придерживаться
этой терминологии и в теоретической
механике. Легко видеть, что механическое
состояние системы, состоящей из двух
частиц, при 
и 
определяется их скоростями (или
импульсами), поэтому векторы 
характеризуют
In-состояния,
а векторы
-Out-состояния
системы. Кроме того нужно также задать
массы частиц 
,
энергию их взаимодействия 
и параметр 
,
называемый прицельном расстоянием.
Скорости
частиц задаются относительно некоторой
инерциальной системы отсчета, которую
в теории рассеяния обычно называют
лабораторной системой или л-системой.
Если рассматривается задача о рассеянии
двух пучков частиц (в таком случае
предполагается, что в одном из пучков
все частицы имеют одинаковые массы,
скажем 
,
и скорости
,
а во втором 
и 
то, как будет видно из дальнейшего, нужно
также задать угол 
определяющий ориентацию плоскости
движения каждой из пар относительно
системы отсчёта, связанной с центром
масс какой либо пары (эту систему называют
ц-системой).
Задачу
рассеяния двух частиц можно решать в
общем виде, используя полученное выше
решение задачи двух тел. В самом деле,
задачу двух тел сведём к задаче о движении
-точки
и далее, учитывая сохранение скорости
центра масс рассматриваемой системы в
процессе рассеяния (вследствие того,
что система изолированная), находим
,
(1.6)
где
- скорость центра масс, а 
скорость 
-точки
после рассеяния. Величину 
найдем из закона сохранения энергии
для 
-точки
(закон сохранения энергии в задаче двух
тел относительно ц-системы):
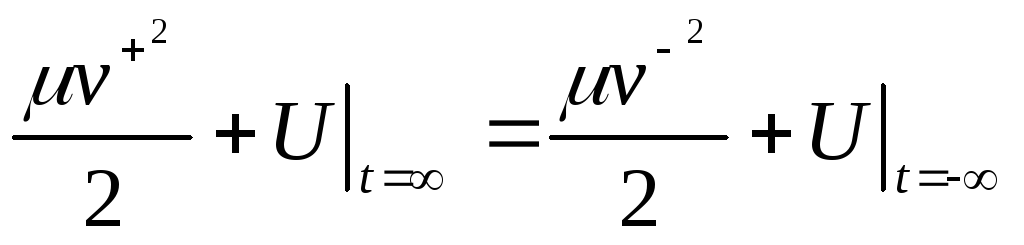. (2.6)
Но
так как 
.
Поэтому 
,
где 
,
а единичный вектор 
направлен по 
или 
.
Процесс
рассеяния в ц-системе
можно изобразить графически (рис. 1.6) на
плоскости 
,
являющейся
плоскостью движения взаимодействующих
частиц. Напомним, что если 
как на рис. 1.6, то согласно (38.5)
,
где
-радиус – вектор 
-точки.
Так
как в ц-системе
в любой момент времени 
(и, значит, 
и 
),
то угол между 
и 
равен углу между 
и 
и, следовательно, скорости частиц в
любой момент 
направлены противоположно. Таким
образом, результат упругого рассеяния
частиц сводится в ц-системе
к повороту скоростей обеих частиц,
остающихся взаимно-противоположными
и неизменными по величине. Но так как
вектор 
параллелен 
,
этот угол равен углу отклонения 
-точки.
Обозначим
угол отклонения буквой 
.
Учтём, что полярный угол 
выражается через определенный интеграл:
,
(3.6)
где
точка поворота 
является корнем уравнения
.
В
подынтегральное выражение (3.6) входят
параметры, характеризующие 
-точку.
Очевидно, что
. (4.6)
Мы
здесь воспользовались общим свойством
симметричности траектории по отношению
к прямой, проведенной в ближайшую к
центру поля точку орбиты. Поэтому обе
асимптоты орбиты скажем,
-точки,
пересекают указанную прямую под
одинаковыми углами. Угол 
называют
углом рассеяния в системе центра масс;
он равен углу между двумя асимптотами
к траектории 
-точки,
а 
- угол между асимптотой траектории и
апсидальным вектором.
Прицельное расстояние - это расстояние между асимптотами траекторий частиц в ц-системе, по которым частицы движутся до рассеяния. Его также можно определить как минимальное расстояние, на котором частицы пролетели бы друг от друга в отсутствие взаимодействия между ними.
В
задаче рассеяния сохраняющиеся величины
и 
принято
записывать через скорость 
и прицельное расстояние 
:
,
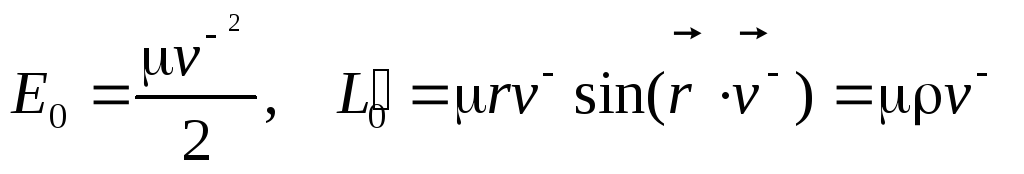так
как 
Отсюда видно, что 
равно длине перпендикуляра, опущенного
из центра поля на асимптоту траектории
-точки,
или, эквивалентно, это минимальное
расстояние, на котором 
-точка
прошла бы от центра если бы взаимодействие
между ней и полем отсутствовало бы
вообще.
Формулами
(1.6), (4.6) дается решение задачи об упругом
рассеянии двух частиц. Мы видим, что эта
задача является лишь частным случаем
задачи двух тел, когда нужно знать лишь
скорости частиц после рассеяния при 
.
Угол рассеяния 
зависит лишь от 
,
,
а так же от вида взаимодействия частиц
и параметров, которые его характеризуют,
т.е. от 
. (5.6)