12.3. Углы эйлера

Теорема Эйлера позволяет представить произвольный поворот твердого тела как последовательность трех поворотов вокруг заданных осей. В кинематике твердого тела распространена система параметров, задающих такие повороты, называемая углами Эйлера. В этом случае матрица произвольного поворота в заданном базисе представляется в виде произведения трех матриц, каждая из которых зависит только от одного параметра.

Пусть - орты лабораторной системы, а- орты системы, связанной с твердым телом, как показано на рис. 1.12. Предполагается, что система ортовпервоначально совпадала с лабораторной системой, а затем была приведена в указанное состояние путем последовательных поворотов, выполненных в следующем порядке.

1. Поворот вокруг оси на угол. При этом ортзаймет положение в плоскостиXY, определяемое на рисунке ортом(пунктир). Этот орт определяет линию узлов, а уголназываетсяуглом прецессии.

2. Поворот твердого тела вокруг орта(оси узлов) на угол. При этом ортзаймет положение, указанное на рисунке, а ортвыйдет из плоскостиOXY. Уголназываетсяуглом нутации.

3. Поворот вокруг орта на уголтак, что ортвыйдет из плоскостиOXY. Уголназываетсяуглом собственного вращения.

Рис. 1.12

Поскольку каждый поворот характеризуется простой матрицей поворота вокруг одной из осей, матрицу полного поворота легко получить как произведение этих матриц.

Первое преобразование определяется матрицей поворота вокруг орта на угол(6.12):

Поворот вокруг линии узлов, оставляющий неподвижным орт , определяется матрицей:

Последнее преобразование - поворот вокруг орта на угол- описывается матрицей, устроенной также, как и матрица:

Результирующий поворот определяется матрицей , равной произведению матриц, взятых в той последовательности, в которой выполнялись повороты:

,

или в тензорных обозначениях

.

Выполняя вычисления, получим выражение для матрицы поворота:

(9.12)

Для выполнения обратного преобразования достаточно взять транспонированную матрицу.

12.4. Угловая скорость твердого тела

Если рассматривать малые повороты, матрица которых близка к единичной

, где,

то матрицу можно считать антисимметричной:

. (10.12)

Это следует из условия ортогональности преобразования (a), которое приводит к уравнению

,

из которого с точностью до линейных по членов и вытекает условие (10.12).

В отличие от конечных поворотов, результат последовательных малых поворотов не зависит от порядка их выполнения. Это вытекает из того, что произведение матриц малых поворотов не зависит от порядка сомножителей с точностью до линейных членов, т. е. эти матрицы с указанной точностью коммутируют.

Как следует из (7.12), координаты точки Mтвердого тела, заданные относительно лабораторной системы, при малых поворотах преобразуются с помощью матрицы:

.

Очевидно, что закон преобразования справедлив для любого вектора, заданного фиксированными координатами в системе, связанной с твердым телом, а не только для радиус-вектора какой-либо точки твердого тела.

Антисимметричный тензор имеет лишь три отличные от нуля компоненты, поэтому ему можно сопоставить вектор, точнее псевдовектор, компоненты которого в лабораторной системе определены соотношениями

.

Их удобно записывать в тензорном виде, вводя единичный антисимметричный псевдотензор третьего ранга , определяемый в любом базисе следующими равенствами:

,

,

а остальные компоненты тензора равны нулю.

Из этого определения вытекают следующие соотношения, полезные для приложений:

(11.12)

.

Используя введенный тензор, псевдовектор можно записать как сверткуи тензора:

. (12.12)

Если твердое тело подвергается двум последовательным малым поворотам, которым сопоставлены векторы исоответственно, то результирующий поворот описывается суммой, которая, в соответствием с правилами сложения векторов, не зависит от порядка выполнения поворотов:

.

Использование тензора упрощает алгебраические операции над векторами. Так, векторное произведение двух векторовис помощью введенного тензора представляется в виде свертки

.

Соответствие между антисимметричным тензором и векторомвзаимно однозначное, так что псевдовекторусоответствует тензор

. (13.12)

Справедливость этого равенства легко доказывается прямой подстановкой, с учетом соотношения (11.12).

Учитывая приведенные выражения, запишем приращения компонент радиус-вектора точки M твердого тела, вызванные его поворотом:

или в векторной форме

.

Приведенные соотношения позволяют ввести вектор угловой скорости,

.

С помощью этого определения вектор скорости точки M твердого тела можно вычислить как векторное произведение:

(14.12)

Угловая скорость является псевдовектором, однако в классической механике принято называть эту величину вектором, так как преобразование инверсии в кинематике твердого тела не рассматривается. Формула, определяющая распределение скоростей точек произвольно движущегося твердого тела, называется формулой Эйлера. Полученная формула (14.12) является частным случаем формулы Эйлера, соответствующим движению тела с одной неподвижной точкой.

Очевидно, что соотношение (14.12) распространяется на любые векторы , проекции которых на ортыостаются постоянными при вращении твердого тела. В частности, это соотношение справедливо и для ортов, связанных с твердым телом:

. (15.12)

С помощью псевдотензора это соотношение может быть записано в форме:

, (16.12)

где - компоненты вектора угловой скорости в системе, связанной с твердым телом.

Отсюда легко определить компоненты вектора угловой скорости, по заданной матрице поворотов .

Действительно, если матрица поворотов зависит от времени, то ориентация ортов изменяется по отношению к лабораторной системе с течением времени по закону:

.

Дифференцируя это выражение по времени (при постоянных ортах ), и переходя с помощью обратной матрицы от ортовк ортам, получим:

.

Сравнивая это выражение с (16.12), придем к соотношению:

.

Умножая его на и проводя суммирование по повторяющимся индексамi, mс помощью соотношения (14.12), найдем явное выражение для компонент вектора угловой скорости (в системе, связанной с твердым телом)

.

Этот же результат можно получить непосредственно из соотношения ортогональности (7.12), дифференцируя его по времени:

.

Отсюда следует, что тензор является антисимметричным:

,

что позволяет ввести вектор , характеризующий скорость изменения ориентации ортов при движении твердого тела, путем свертки этого тензора с псевдотензором:

,

который совпадает с вектором угловой скорости,введенным ранее.

Учитывая связь между компонентами антисимметричного тензора и псевдовектора (13.12), с помощью соотношений (14.12) можно записать выражение для скорости изменения ортов подвижной системы в виде, совпадающем с полученным ранее (+):

.

Если компоненты матрицы поворотов зависят от некторых параметров- обобщенных координат, то компоненты вектора угловой скоростиопределяются выражением:

.

В частности, для углов Эйлера это дает

.

Приведенное выражение, позволяющее вычислить компоненты вектора угловой скорости для произвольной матрицы поворота, довольно громоздко. Если же поворот может быть представлен как последовательность элементарных поворотов вокруг заданных осей, то удобнее вычислять угловую скорость, пользуясь принципом суперпозиции. Так, для углов Эйлера угловую скорость можно представить в виде суммы:

,

где слагаемые равны, соответственно,

,,,

а орт может быть представлен в виде:

.

Таким образом, вектор угловой скорости представляется суммой

. (17.12)

При составлении динамических уравнений удобно использовать вектор угловой скорости, определенный проекциями на орты движущейся системы:

.

Учитывая, что , где матрица поворотов дается выражением (9.12), а, получим явный вид компонент вектора угловой скорости:

,

,

. (18.12)

Аналогичным образом с помощью представления (17.12)) можно вычислить и проекции вектора угловой скорости на орты лабораторной системы. В этом случае они определяются следующим образом:

,

,

. (19.12)

Полученные выражения называются кинематическими уравнениями Эйлера.

12.5. ПОЛЕВОЙ ПОДХОД К ОПИСАНИЮ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Движение твердого тела можно описывать в модели сплошной среды, предполагая, что кинематические характеристики ее являются полевыми переменными. Такой подход позволяет использовать при описании движения твердого тела дифференциальный аппарат теории поля. Воспользуемся для описания сплошной среды методом Эйлера. Предположим, что в окрестности любой точки пространства можно указать такой объем, что физические характеристики среды с заданной точностью либо не зависят от формы, размеров и способа выделения этого объема, либо пропорциональны величине этого объема. Такой объем называется элементарным. Во втором случае вводится коэффициент пропорциональности, не зависящий от элементарного объема, называемый плотностью физической величины. Физические величины или их плотности, относящиеся к данному элементарному объему, зависят лишь от положения точки наблюдения и образуют поля физических величин.

Пусть движение сплошной среды происходит так, что в любой точке пространства в каждый момент времениtсуществует элементарный объем, в котором скорость движущегося вещества с заданной точностью можно считать одинаковой. В таком случае в пространстве можно ввести поле скоростей движущейся среды:

.

Если движущаяся среда является твердым телом, то для любых двух ее точек, принадлежащих элементарным объемам и, для любогоt справедливо равенство (1.12).

Будем считать поле скоростей дифференцируемой функцией своих аргументов. В линейном по приближении это приведет к условию недеформируемости сплошной среды в дифференциальной форме:

.

Выполнение этого условия для любых возможно в двух случаях.

1. Вектор скорости не зависит от координат:

.

В этом случае все точки твердого тела движутся с одинаковыми скоростями. Такое движение называется поступательным.

2. Движение не является поступательным.

Поскольку тензор является симметричным, то в этом случае тензорявляется антисимметричным для любой точки сплошной среды, то есть:

.

Сопоставим антисимметричному тензору псевдовектор, образующий векторное поле:

или в векторных обозначениях

.

Для твердого тела поле вектора не зависит от координат, то есть является глобальной характеристикой движения. Чтобы показать это, вычислим его производную по координатам:

.

Но тензор является антисимметричным в любой точке:

, (20.12)

что удобно представить в явной форме:

.

Выполняя дифференцирование этого тензора с учетом условия (20.12) получим:

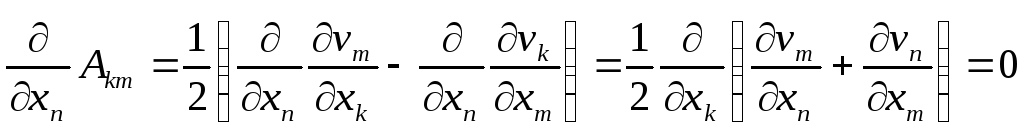
Отсюда следует, что вектор скорости может быть только линейной функцией координат:

.

Учитывая, что , этому соотношению можно придать следующий вид:

.

Векторная форма этого соотношения

известна как формула Эйлера, частный случай которой был получен нами ранее (14.12). Таким образом, введенный нами векторявляется вектором угловой скорости, введенным ранее.

Если движение твердого тела является вращением, при котором скорость одной из его точек остается равной нулю

,

то вектор в любой момент определяет ось вращения, проходящую через начало координат. Такая ось называетсямгновенной осью вращения.

Она описывает в пространстве коническую поверхность, называемую неподвижным аксоидом. Коническая поверхность, которую ось вращения описывает относительно твердого тела, называется подвижным аксоидом. Эти поверхности в любой момент времени касаются друг друга по образующей, которая совпадает с мгновенной осью вращения.

Если при произвольном движении твердого тела известны скорость и его угловая скорость, то для случаяформула Эйлера позволяет определить положения точек твердого тела, скорость которых в данный момент времени равна нулю, то естьмгновенных центров вращения :

.

Рассмотренный случай реализуется, в частности, при плоском движении твердого тела, когда вектор любой точки в любой момент времени лежит в плоскости, неподвижной относительно лабораторной системы.