14.1. Элементы теории возмущений

Рассмотрим консервативные одномерные системы. Динамические уравнения для этих систем имеют первый интеграл — интеграл энергии, что позволяет провести качественный анализ характера движения и записать формальное выражение для закона движения точки в виде

(1.14)

Здесь —начальная координата, а параметр —энергия, определяемая начальными условиями.

Аналитическое представление закона движения связано с возможностью выполнить интегрирование, т. е. представить решение в виде элементарных или специальных функций, свойства которых хорошо известны. Представление закона движения в явном виде связано с дополнительной возможностью обращения полученных функций.

Ясно, что это возможно лишь в исключительных случаях для ограниченного класса функций и, как правило, при некоторых определенных значениях энергии,т. е. лишь при определенных значениях начальных условий. Будем называть задачу, допускающую представление решения в таком виде, невозмущенной, а соответствующее решение — невозмущенным решением:

.

Практический интерес представляет построение решения в виде «простых» комбинаций невозмущенных решений при некотором «малом» изменении потенциальной энергии. Будем считать, что потенциальная энергия может быть представлена в виде

(2.14)

где параметр — «малый» параметр, который может быть связан с некоторым «малым» параметром, характеризующим отклонение от невозмущенного решения.

Назовем такую систему возмущенной, а слагаемое — возмущением. В частности, возмущение может иметь вид, что соответствует изменению только начальных условий задачи без изменения сил, действующих на точку.

Теория возмущений изучает методы построения решений возмущенной задачи с заданной точностью в некоторой области изменения времени в виде простых комбинаций определенных функций.

Предположим, что возмущенное решение

при стремится всюду в области изменения переменнойк невозмущенному решению ,т. e. выполняется условие

при

для всех из указанной области.

Возмущенные решения, обладающие такими свойствами, называются регулярными. Возмущения, не обладающие этим свойством, называют сингулярными.

Возмущенное решение мы будем представлять с помощью удобных для анализа «простых» функций

,

которые при могут отличаться от возмущенного решенияна некоторую величину.

Если при отличие исчезает, т. e.

при,

то функции называют асимптотическим приближением возмущенного решения, а соответствующая теория является асимптотической теорией возмущений. Для оценки отклонения возмущенного решения от невозмущенного удобно представить решение в виде функционального ряда по параметру возмущения:

.

Функции могут быть любыми ограниченными функциями (кроме ,но обычно в качестве таких функций выбирают решение невозмущенной задачи или функции, получаемые из этих решений с помощью последовательного интегрирования или дифференцирования. Конкретные методы построения таких функций определяют ту или иную теорию возмущений.

Мы будем рассматривать такие ряды, что N-я частичная сумма ряда

является асимптотическим приближением возмущенного решения, причем приближением с точностью порядка , т. е.

Если ряд является сходящимся при рассматриваемых значениях параметра возмущения в некоторой области изменения, то увеличениеNприводит к увеличению точности представления возмущенного решения.

Асимптотическое представление возмущенного решения возможно и с помощью расходящегося ряда. Если ряд расходится при выбранном значении возмущения , то частичные суммы могут быть устроены так, что при точность представления возмущенного решения возрастает, и лишь начиная с некоторого номера точность падает.

Асимптотические ряды могут быть использованы для оценки или вычисления квадратур вида (1.14), возникающих при интегрировании уравнений движения консервативных систем. рассмотрим один из методов построения асимптотического ряда для такой задачи и обсудим условия сходимости. Пусть решение возмущенной задачи представлено в виде квадратуры:

. (3.14)

Предположим, что в рассматриваемой области изменения переменных подынтегральное выражение определено в каждой точке, т. e. всюду в этой области выполняется условие

.

Предположим, что в этой области существует невозмущенное решение, удовлетворяющее аналогичным условиям.

Представим подынтегральное выражение в виде произведения

.

Второй сомножитель этого произведения может быть представлен в виде формального ряда, так что подынтегральное выражение имеет вид

, (4.14)

что приводит к выражению

.

Если закон движения в отсутствие возмущения ,то учет поправки дает неявное выражение для возмущенного движения

.

Неявное уравнение можно решить методом итераций, если мало Первая итерация дает

так что

Замечательно, что эта формула может быть использована и вблизи от точки остановки, хотя интеграл в этой точке расходится, так что разложение (4 14) оказывается неприменимо

Конечно, представление решения в виде ряда целесообразно лишь в тех случаях, когда вычисление членов этого ряда проще, чем интеграла (3.14).

В системах, совершающих колебания, часть времени частица проводит вблизи точек остановки , где подынтегральное выражение имеет особенность, так как

.

Мы будем считать, что и в возмущенной и в невозмущенной задачах точки остановки находятся вдали от точек равновесия, так что .Соответственно для возмущенной задачи точки остановки определяются уравнением

,

и мы предположим, что

.

Рассмотрим возможность применения теории возмущений вблизи особых точек для определения периода колебаний возмущенной системы. Период колебаний невозмущенной системы определяется выражением

.

Для определения периода колебаний возмущенной системы не обходимо вычислить интеграл

Предположим, что возмущение достаточно мало, так что всюду в области интегрирования выполняется условие равномерной сходимости ряда

которое нарушается лишь в граничных точках, где

.

Подынтегральное выражение может быть разложено в ряд, однако условия теоремы о дифференцируемости интеграла по параметру в особых точках нарушаются. Это приводит к нарушению условий сходимости ряда в точках ,поскольку прив случае

.

Биномиальный ряд, представляющий второй сомножитель в выражении (4 14), имеет радиус сходимости ,так что при выполнении условия

(5.14)

подынтегральное выражение представлено равномерно сходящимся рядом. Неравенство позволяет в заданной области изменения координаты определить величину параметра возмущения, обеспечивающего равномерную сходимость Если возмущение задано, то это неравенство определяет область изменения координат, где ряд сходится равномерно.

Равномерно сходящийся ряд можно интегрировать почленно, поэтому при выполнении условия (5.14) решение возмущенной задачи может быть представлено в виде

.

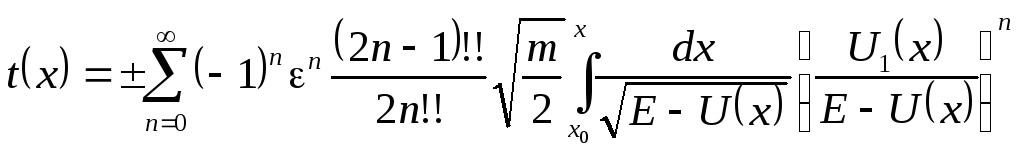Мы предполагаем, что функции, представляющие закон движения невозмущенной задачи ,позволяют представить с помощью простых функций В этом случае решение представляется сходящимся рядом

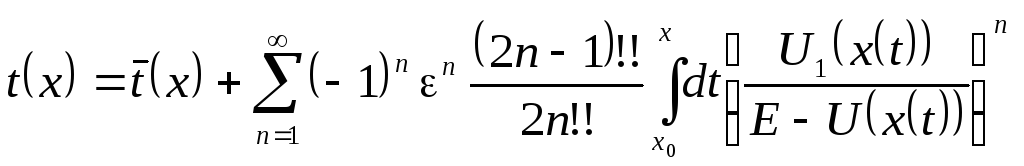(6.14)

Здесь проведена замена переменной

.

Для оценки получающихся интегралов удобно использовать тождество

.

При дифференцировании верхнего и нижнего пределов мы учли, что

.

С помощью этого тождества период возмущенного движения может быть представлен в виде

Предполагая, что всюду в области выполнено условие разложимости в ряд, получим для оценки периода выражение

Пустьдля определенности всюду в области Тогда, a ,т е точки лежат за границами области возможного движения возмущенной задачи Поскольку мы предполагаем, что , при вычислении интегралов от первой суммыпределы интегрированияможно заменить на, причем ошибка вычисления интеграла при такой замене будет порядка.'

Аналогичная оценка может быть получена для любой функции ,достаточно гладкой и удовлетворяющей условию.

При интегрировании второй суммы нельзя изменить пределы интегрирования для каждого слагаемого, однако эта сумма при сделанных предположениях не превышает слагаемого при . Таким образом, с помощью полученного выражения мы имеем асимптотическое представление периода

Переходя к пределу , имеем

.

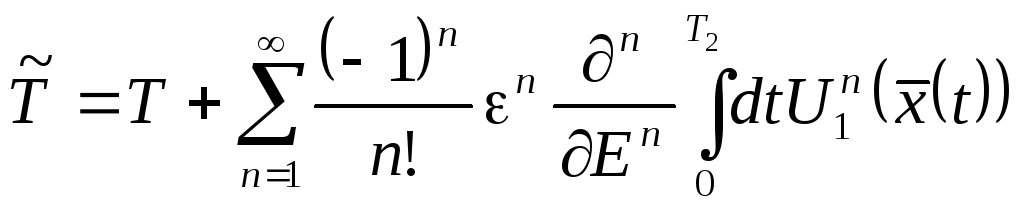Здесь Т —период невозмущенного движения, —закон движения точки в невозмущенной задаче.

Вообще говоря, условие равномерной сходимости существенно, но не является необходимым для почленного интегрирования ряда, так что при указанных условиях ряд теории возмущений будет сходящимся

В практически важном случае, когда

,

уравнение движения оказывается линейным, а закон невозмущенного движения представляется элементарной функцией

, где .

В этом случае изменение периода вычисляется особенно просто:

. (7.14)

В качестве примера применения изложенного метода вычислим период колебаний системы, полагая

,

Невозмущенное движение — гармонические колебания, период которых , а закон движения

где .

Выражение для периода колебаний в этом случае представляется рядом

.

Интеграл легко берется

,

так что выражение для периода приводится к виду

. (8.14)

При выполнении условия полученный ряд сходится и сумма его вычисляется:

Отсюда следует, что период возмущенного движения при условии выражается формулой

,

т. е. совпадает с точным выражением.

При полученный ряд расходится, однако в областион может быть использован для оценки периода колебаний, поскольку остаточный член ряда сначала убывает с ростом.

|

Остаточный член ряда может быть представлен в виде

,

где,.Таким образом, хотя ряд расходится, при любомвыполняется условие

,

т. е. ряд является асимптотическим представлением функции

.

При ряд является знакопеременным, так что остаточный член ряда не превышает первого отброшенного члена. Это приводит к тому, что увеличение точности представления функции в области, где ряд расходится, происходит с ростомлишь до тех пор, пока члены ряда удовлетворяют условию

.

Это отношение убывает для всех целых ,удовлетворяющих неравенству

,

где —целая часть числа.

Поведение суммы первых членов ряда для случая иллюстрирует рис. 1.14.

Рассматриваемые свойства асимптотического ряда вызваны тем, что ряд, заданный своими коэффициентами, определяет функцию неоднозначно. Можно показать, что две функции, представляющиеся асимптотическими рядами, коэффициенты которых одинаковы, могут отличаться на экспоненциально малую величину. Такая погрешность, не представимая степенными рядами, может существенно менять характер поведения решения динамических уравнений.

Вернемся к ряду (8.14), представляющему поведение периода колебаний осциллятора. Поскольку в области асимптотический ряд может быть использован лишь для определения границ области, в которой находится решение, выберем для каждогооптимальное значение членов ряда, чтобы минимизировать ошибку

,

и построим границы области, внутри которой может находиться функция, представляемая этим рядом. Это построение иллюстрирует рис. 2.14. В области сходимости ряда теории возмущений определена функция .За пределами этой области ряд не представляет определенной функции. Решение исходной задачи в этой области может оказаться достаточно «простым», а может быть и таким, что представление его с помощью элементарных функций и их комбинаций невозможно. Эти выводы полностью переносятся на асимптотические ряды, коэффициенты которых являются функциями времени и представляют закон движения точки. Очень сложное поведение решений динамических уравнений в области неустойчивости и явления динамического хаоса как раз и дают примеры явлений, не описываемых в рамках такого подхода.

Во многих случаях ряды теории возмущений используются лишь для оценки характера решения и его зависимости от параметров, поэтому часто достаточно ограничиться лишь первыми членами разложения асимптотического ряда. Такой подход можно проиллюстрировать на примере математического маятника. Определим в первом порядке теории возмущений поправку к периоду колебаний математического маятника. Интеграл энергии для маятника

(9.14)

приводит к формальному выражению для закона движения

. (10.14)

Будем рассматривать такие значения энергии

, где(11.14)

что в области возможных движений можно ограничиться лишь первыми членами разложения потенциальной энергии, полагая

.

Остаточный член знакопеременного ряда удовлетворяет условию , что дает при.Поправка к потенциальной энергии

,

что приводит к выражению для периода в первом порядке по :

.

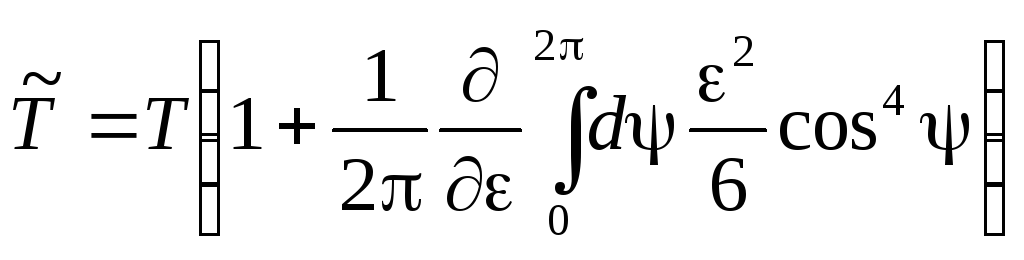Вычисляя интеграл и выполняя дифференцирование по , Имеем

.

Отметим еще раз, что рассматриваемая теория возмущений неприменима вблизи точек локального максимума потенциальной энергии.

Пользуясь полученными результатами, можно вычислить не только поправку к периоду колебаний, но и поправку к закону движения. Подставляя в формулу (10.14) выражение (11.14) ;ля потенциальной энергии возмущений, в первом порядке малости получим искомое выражение

.

Здесь мы предполагаем, что начальные условия выбраны в виде

,.

Учитывая, что невозмущенное движение — гармонические колебания

, где,

проведем замену переменных в интеграле, полагая .

.

Интеграл легко вычисляется, так что поправка к закону движения имеет вид

.

Учитывая сделанную замену переменной, мы имеем зависимость

.

Закон движения с учетом поправки можно получить в явном виде, используя итерацию:

что приводит к окончательному результату

. (12.14)

При формула (12.14) неприменима.

Обобщение можно получить, полагая, что движение периодическое, как это следует из теории качественного исследования, а непериодические «секулярные» члены возникли в результате разложения периодических функций. Это позволяет предполагать, что возмущенное движение описывается выражением

, (13.14)

где .

Таким образом, применение теории возмущений позволяет сделать вывод, что появление высших членов разложения потенциальной энергии вблизи точки локального минимума приводит к изменению периода колебаний и, значит, изменению основной частоты. Вторым эффектом является возникновение гармоник этой новой частоты.