Адиабатические инварианты
Важным
свойством переменных действия является
свойство адиабатической инвариантности,
которое заключается в том, что переменные
действия сохраняют свои постоянные
значения и в тех случаях, когда гамильтониан
системы зависит от времени через
некоторые параметры 
,
которые, как говорят, адиабатически
меняются со временем, т. е. очень медленно.
Под медленными подразумеваются такие
изменения, при которых 
мало меняются за отрезки времени, равные
по порядку величины периодам 
,
т. е.
(61.11)
Ясно, что такие механические системы не являются строго изолированными. Покажем, что переменные действия в таких системах являются адиабатическими инвариантами.
Рассмотрим
систему, совпадающую в каждый момент
времени с изученной выше консервативной
системой, которая допускает полное
разделение переменных. Предполагаем
также, что движение системы финитно.
Гамильтониан такой системы явно зависит
от параметров 
,
которые удовлетворяют условиям (61.11);
его можно представить в виде
(62.11)
При
постоянном 
являются периодическими функциями
соответствующих координат 
;
в данном
случае являются периодическими функциями
времени.
Если
параметры 
меняются со временем медленно, то,
несмотря на то что система, описываемая
гамильтонианом (62.11) не консервативна,
решение уравнения Гамильтона-Якоби
можно искать в виде, близком к (24.11):
(63.11)
где,
однако, параметры 
,
а поэтому и величины 
и 
медленно меняются со временем. Подставляя
(63.11) в уравнение Гамильтона-Якоби и
пренебрегая в нем членами, пропорциональными
,
получим уравнение «нулевого приближения»
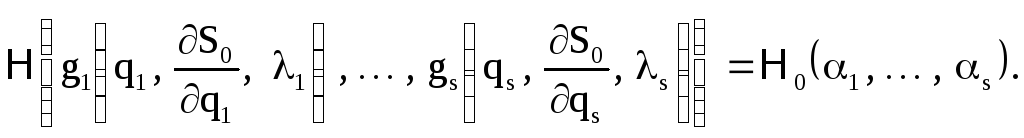(64.11)
В
силу (61.11) это уравнение можно решать,
полагая все 
постоянными, и лишь в построенных
решениях считать их заданными функциями
времени. Поэтому все формулы, полученные
выше для консервативной системы остаются
справедливыми, но во все соотношения
теперь войдут зависящие от времени
параметры 
.
Производящая
функция канонического преобразования
от переменных 
к переменным 
определяется функцией 
,
которая теперь, однако, будет зависеть
и от 
:
(65.11)
Заметим,
что 
также зависят от 
.
Напишем формулы канонического преобразования, генерируемого функцией (65.11):
(66.11)
(67.11)
(68.11)
Новые уравнения движения имеют вид
(69.11)
(70.11)
Во
всех формулах дифференцирование по 
должно производиться при постоянных 
и 
;
после дифференцирования в формулах
(69.11), (70.11) выполняется подстановка
(67.11) и
производные
выражаются через 
.
Для
доказательства свойства адиабатической
инвариантности переменных 
усредним
уравнения (70.11) по интервалу времени,
малому по сравнению со временем заметного
изменения параметров 
и достаточно большому по сравнению с
периодами системы. При таком выборе
интервала времени величины 
(в силу
медленного изменения 
)
можно выносить из-под знака среднего.
Следовательно,
(71.11)
Покажем
теперь, что производные 
являются однозначными периодическими
функциями 
.
Если это так, то тогда их можно будет
разложить в ряды Фурье, коэффициенты
которых будут зависеть от 
и 
.
В свою очередь ряды Фурье для производных
не будут содержать постоянных членов,
и поэтому при усреднении по достаточно
большому интервалу времени все производные
обратятся в нуль и адиабатическая
инвариантность всех 
будет
доказана.
Заметим,
что 
- неоднозначная функция координат 
,
так как
согласно (66.11) ее можно представить в
виде
(72.11)
За
полный период изменения координаты 
(при остальных фиксированных) 
получает приращение
(73.11)
Функции
- однозначные функции координат, так
как при дифференцировании по 
добавки, кратные 
,
которые
приводят к неоднозначности 
,
исчезнут. Так как 
- однозначные функции координат 
,
то они
являются периодическими функциями
угловых переменных 
;
эти функции не будут менять свои значения
при изменении 
на
(при заданных значениях
).
Иными словами,
любая однозначная функция
,
выраженная через канонические переменные
является периодической функцией каждой
с периодом,
равным 
.
Итак все 
являются однозначными периодическими
функциями 
.
Выше мы показали, что в этом случае все
и, значит,
все
Свойство адиабатической инвариантности всех переменных действия доказано.
Пример. Как изменится энергия заряженной частицы е массы т в центральном поле U(r) при медленном включении слабого однородного магнитного поля напряженности Н?
Запишем функцию Гамильтона заряда в сферической системе координат (ось Oz декартовой системы координат параллельна H):
Здесь
-
скорость света. По условию задачи
магнитное поле слабое, поэтому последним
членом (квадратичным по H)
пренебрегаем.
Уравнение Гамильтона-Якоби с учетом этого приобретает вид
(74.11)
где
- энергия частицы, 
-циклотронная частота.
Решение ищем в виде
Здесь
в качестве постоянной 
мы выбрали 
.
Подставляя 
в (74.11),
получаем
(75.11)
(76.11)
Уравнение
(75.11) определяет функцию 
которая нужна для вычисления переменной
действия 
:
Очевидно,
будет совпадать с 
,
вычисленным для случая 
,
если в последнем выражении вместо 
подставить комбинацию 
Значит, величина 
остается постоянной при медленном
включении однородного магнитного поля.
Кроме нее постоянной будет величина 
- компонента обобщенного импульса
заряда. По физическому смыслу 
- сохраняющаяся проекция момента импульса
заряда на вектор H.