11.6. Переменные «действие - угол»

Рассмотрим консервативную механическую систему и предположим, что существует хотя бы один набор канонических переменных, в котором все переменные разделя­ются. Это нужно понимать так: можно отыскать канонические переменные, в которых решение уравнения Гамильтона-Якоби примет вид (24.11). Далее предположим, что исследуемые нами механические системы могут совершать движения, близкие к периодическим: мы рассматриваем такие движения, в которых либо каждая из переменных является периодической функцией времени с одинаковым периодом, либо каждый импульс является периодической функцией координаты , в то время как сама координата не является периодической функцией времени. В первом случае движение называют либрацией, во втором - вращением. Нелишне также подчеркнуть, что здесь и есть тот самый набор канонических переменных, в котором переменные в уравнении Гамильтона-Якоби полностью разделяются.

Заметим, что механические системы, в которых реализуются вышеупомянутые движения, не столь редки. Есть системы, в которых возможны оба движения – либрация и вращение – в зависимости от того, какая область значений параметров и начальных значений реализуется. Проекция фазовой траектории такой системы на соответствующую плоскость качественно изображена на рис. 2.11.

Уравнение Гамильтона-Якоби для рассматриваемых нами систем имеет вид

(37.11)

причем

(38.11)

(39.11)

(40.11)

Канонические импульсы , определяемые соотношениями

(41.11)

зависят только от и являются периодическими функциями этой же координаты. Весьма плодотворной является идея перехода к таким «новым» каноническим переменным, в которых «новые» импульсы были бы постоянными движения , зависящими от постоянных :

(42.11)

а все «новые» координаты были бы циклическими, т. е. «новый» гамильтониан зависел бы только от импульсов

(43.11)

Из (41.11) видно, что в качестве можно выбрать

(44.11)

где интегралы берутся по полным периодам изменения импульсов как функций соответствующих координат.

«Новые» переменные являются независимыми функциями , что следует из (42.11):

(45.11)

Их называют переменными действия. Разрешая последние соотношения относительно , получим

(46.11)

Подставляя (46.11) в (40.11), найдем

(47.11)

Укороченное действие после подстановки в него из (46.11) приобретает вид

Но по установленному выше смыслу как функцию можно рассматривать как производящую функцию канонического преобразования к переменным, в которых играют роль импульсов. «Новые» координаты при таком преобразовании можно получить из соотношений

(48.11)

«Новые» координаты мы обозначили буквой ; они называются угловыми переменными.

Канонические переменные называются переменными «действие-угол». Уравнения Гамильтона в этих переменных очень просты:

(49.11)

(50.11)

Из (49.11) с учетом (47.11) получим

(51.11)

Каждая из угловых переменных, как видно, является линейной функцией времени.

Покажем теперь, что величина есть частота изменения импульса . Для этого найдем приращение за полный период изменения при условии постоянства всех других (кроме ) координат:

(52.11)

где - символ Кронекера со значениями С другой стороны,

(53.11)

где - полный период изменения импульса . Сравнивая (52.11) с (53.11), видим, что

(54.11)

откуда следует, что

(55.11)

есть частота изменения импульса.

Фактически мы показали, что для нахождения частот нет необходимости решать динамическую задачу, т. е. отыскивать . Для определения нужно:

1. определить функции

2. найти переменные действия как функции

3. определить гамильтониан как функцию

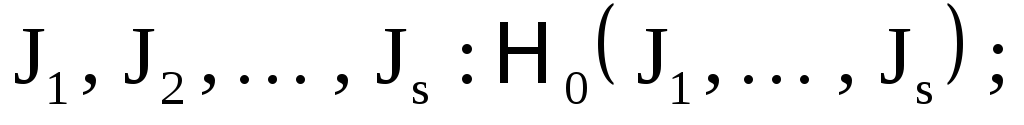
4. найти частные производные

Подчеркнем, что это утверждение относится лишь к системам, которые могут совершать движения, близкие к периодическим в указанном в начале п. 11.6 смысле слова. Движение произвольной механической системы со многими степенями свободы в общем случае не является периодическим ни в целом, ни по каждой из ее координат в отдельности, несмотря на то, что задача о движении этой системы допускает полное разделение переменных в методе Гамильтона-Якоби. Можно показать, однако, что любая однозначная функция механического состояния системы , выраженная через переменные «действие - угол», является периодической функциейс периодом. Поэтому ее можно представить в виде разложения в кратный ряд Фурье вида

Каждый из членов этого ряда является периодической функцией времени с частотой

Весь ряд, однако, не будет представлять собой в целом строго периодическую функцию, если все частоты не кратны какой-либо одной из них. Полагаяили, видим, что последнее замечание относится и ки.

П р и м е р. Определить частоты трехмерного не изотропного осциллятора.

Гамильтониан системы

Уравнение Гамильтона-Якоби для укороченного действия

(56.11)

сводится к трем обыкновенным дифференциальным уравнениям:

(57.11)

(58.11)

(59.11)

При этом

а переменные действия - «новые импульсы» -

(60.11)

Видно, что в соответствующих плоскостях фазовые траектории представляют собой эллипсы с полуосями в плоскости в плоскости в плоскости соответственно. Величины представляют собой площади этих эллипсов, деленные на . Поэтому

и

Следовательно, частоты изменения импульсов равны