15.3. Понятие о структурной устойчивости

Динамические системы, описываемые в рамках метода Лагранжа, испытывают воздействие со стороны внешних тел, задаваемых как силами, так и связями. В ряде случаев зависимость удобно задавать с помощью параметров, входящих в уравнение движения наряду с обобщенными координатами. Зависимость от дополнительных параметров по существу означает, что при описании динамики мы используем различные модели, определяемые выбором соответствующих параметров. Аналогичная ситуация имеет место и при решении задач, когда модель уже выбрана. Как правило, в процессе решения уравнений движения приходится делать некоторые приближения, меняющие исходные уравнения. Эти изменения, приводящие к изменению исходной модели, также могут быть описаны как переход к уравнениям, зависящим от параметров. Наконец, и выбор исходной модели также обусловлен некоторыми приближениями, и при анализе необходимо оценивать последствия неточности модели. Понятно, что физически содержательные результаты при исследовании динамики таких систем будут получены, если некоторые небольшие изменения параметров задачи не приведут к качественным изменениям в поведении системы, т. е. если модель оказывается достаточно «грубой».

Если перейти к описанию движения системы с помощью дифференциальных уравнений вида

,

где — параметры, характеризующие систему, то при изменении параметров возможное изменение характера движения может повлечь изменение структуры фазового пространства рассматриваемой системы.

Как мы отмечали ранее, система динамических уравнений порождает определенную структуру фазовой плоскости, характеризуемую количеством и взаимным расположением особых точек и особых кривых, как содержащих особые точки, так и не содержащих их. Особые кривые определяют топологическую структуру фазового пространства.

Пространство параметров, таким образом, может быть разбито на области, в которых изменение этих параметров не меняет топологической структуры фазового пространства, сохраняя количество и тип особых точек и их взаимное расположение. Изменение топологии, происходящее при некоторых значениях, называют бифуркацией.

Исследование в этом направлении, выполненное в работах А. А. Андронова и Л. С. Понтрягина, привело к уточнению введенных понятий и положило начало математической теории бифуркаций.

Понятие бифуркации системы и грубости опирается на понятие топологической эквивалентности фазового пространства различных динамических уравнений или уравнений при различных значениях параметров.

Системы называют топологически эквивалентными, если существует гомеоморфизм, связывающий две системы: и, т. е.

,

где осуществляет взаимно однозначное соответствие, причем

для любого .

Система является структурно устойчивой, если она порождает в фазовом пространстве топологически эквивалентную систему особых точек и кривых, причем ориентированные фазовые кривые системы топологически эквивалентны в некоторой области изменения параметров.

Структурно устойчивые системы называют грубыми. Системы, не являющиеся грубыми, называют негрубыми. Значения параметров, при которых происходит перестройка структуры фазового пространства, называют критическими.

В общем случае характер изменения фазового пространства чрезвычайно сложен и недостаточно изучен, поэтому мы ограничимся лишь простейшим случаем — рассмотрим фазовую, плоскость.

Рассмотрим автономные системы. В этом случае число особых фазовых траекторий ограничено. Это состояния равновесия, сепаратрисные кривые седловых состояний равновесия и '•замкнутые фазовые траектории. Поскольку рассматриваются лишь грубые системы, то такие кривые, как сепаратрисы, идущие из одной седловой точки в другую, отсутствуют.

Назовем негрубые системы, которые возникают в момент (перехода от одного состояния к другому, системами первой степени негрубости, если в результате изменения параметров появляется только одна особая траектория.

Пусть уравнения движения соответствующим выбором переменных приведены к виду

,.

Рассмотрим простейшие случаи.

Пусть ,.Тогда при уравнения не содержат особых точек, а приимеются две особые точки:

,.

Точка — устойчивый узел, а точка —седло, поскольку оба корня характеристического уравнения в точке 1 отрицательны, а в точке 2 имеют разные знаки. Изменения структуры фазовой плоскости показаны на рис. 6.15.

Бифуркация рождения пары особых точек, одна из которых является седлом, а другая — узлом, называется седло—узел и является примером системы первой степени негрубости.

Другой типичный пример может быть получен, если рассмотреть систему

,.

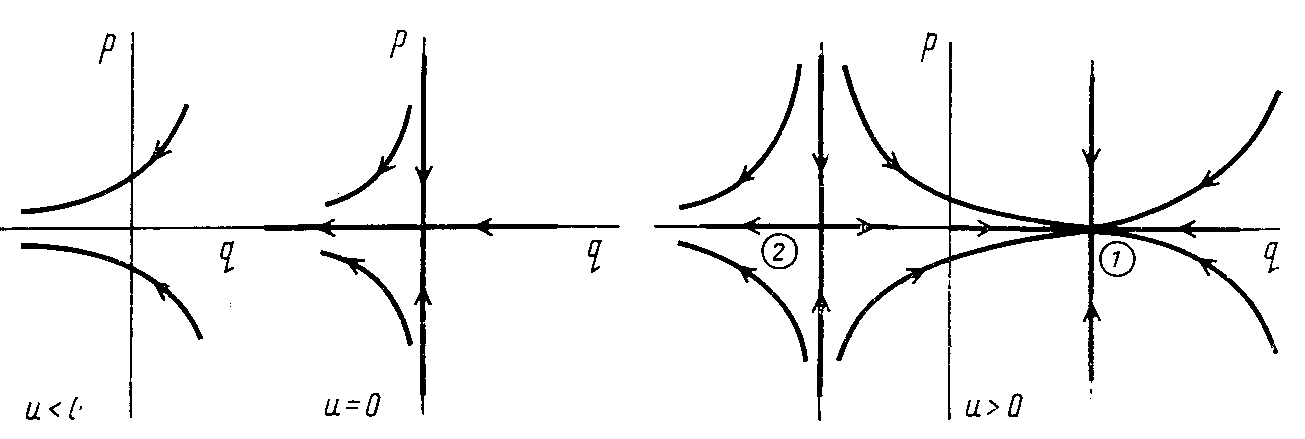
Рис. 6.15

При особая точкаявляется устойчивой особой точкой — это устойчивый узел. Прина фазовой плоскости появляются три особые точки:

,

причем обе точки 1 и 2 являются устойчивыми точками — устойчивыми узлами. Точка пристановится неустойчивой точкой — седлом. Изменение фазовой плоскости в этом случае иллюстрирует рис. 7.15.

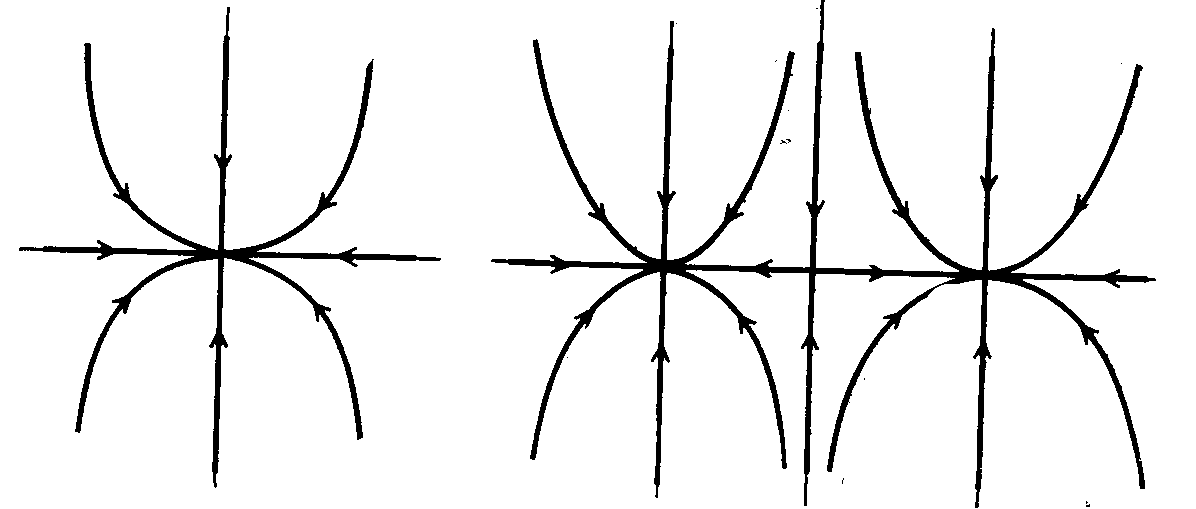
Рис. 7.15

Рассмотрим пример. Пусть центробежный регулятор массы вращается на невесомом стержне длины вокруг вертикальной оси с постоянной угловой скоростью в поле тяжести. Ускорение свободного падения равно .

Введем обобщенную координату — отклонение от положения равновесия (рис. 8.15). Поскольку функция Лагранжа

Рис. 8.15 Рис. 9.15

явно не зависит от времени, сохраняется обобщенная энергия

.

Вводя эффективную потенциальную энергию

,

найдем закон движения

.

Поведение функции существенно зависит от величины угловой скорости. Точки равновесия определяются условием, что приводит к уравнению

,

где .

При всех значениях параметра точкаявляется неустойчивой точкой, где функцияимеет максимум. В точкефункцияимеет либо минимум, если, либо локальный максимум, если. Во втором случае появляется пара локальных минимумов в точках . Вид функцииприведен на рис. 9.15.

При значении всистеме возможны колебания. Прималые колебания происходят около положения, а прималые колебания возможны лишь вблизи точек.Положение равновесияв этом случае становится неустойчивым.

Для анализа структуры фазовой плоскости системы перейдем к каноническим уравнениям, введя импульс . Система канонических уравнений имеет вид

,.

Особые точки фазовой плоскости определяются соотношением между и. Приимеются особые точки,и. Точка,— центр, а точки—седловые. При появляются дополнительные точки покоя, где .

Линеаризуя уравнения в окрестности особых точек, построим матрицу коэффициентов характеристического уравнения

.

Из условия определим собственные значенияи соответствующие им собственные векторы

.

В точке

и при эта точка являются центром. При, так что особая точка — седло. Собственные векторы определяются из условия

,

.

При , так что седловые точки имеют здесь сепаратрисы, определяемые векторами .Структура фазовой плоскости системы до и после бифуркации изображена на рис. 10.15.

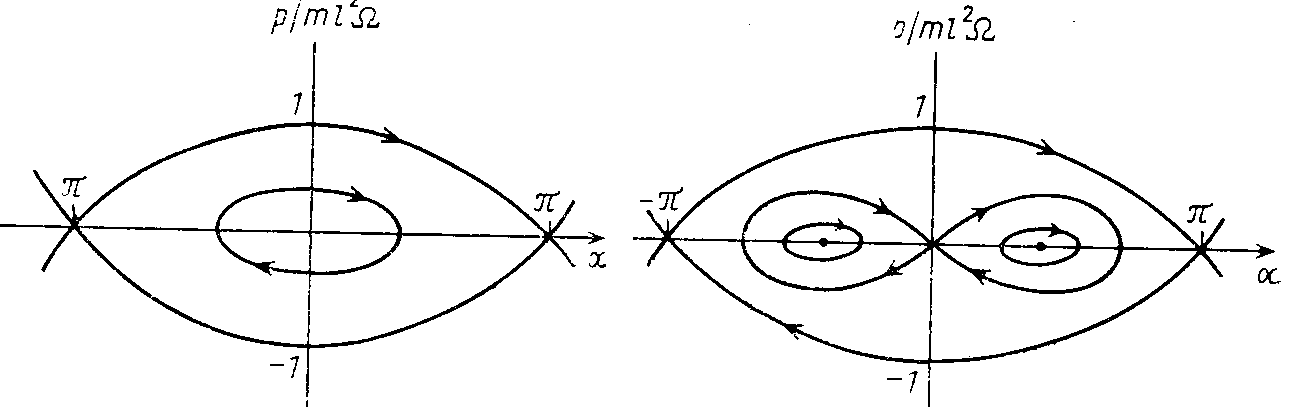
Рис. 10.15

Исследование рассматриваемой динамической системы с трением, пропорциональным скорости, с помощью квадратичного интеграла энергии представляет трудности, так что для анализа этой системы метод фазовой плоскости представляется наиболее удобным. Пусть в системе действует диссипативная сила, пропорциональная скорости .В этом случае обобщенная энергия системы уменьшается:

.

Уравнения движения системы с диссипацией имеют вид

.

Положение особых точек на фазовой плоскости остается неизменным, однако их характер существенно другой. Введение затухания можно рассматривать как некоторый дополнительный параметр. При система является грубой по параметру всюду, за исключением точек бифуркации по, а—критический параметр. При этом значении фокусы переходят в центры. Для определения структуры фазовой плоскости припостроим матрицу линеаризованной системы и характеристическое уравнение

.

Здесь введены параметр () и функция,определенная для особых точек уравнения

.

Корни характеристического уравнения

при определяют устойчивые фокусы.

При особые точки будут или устойчивыми узлами, если оба корня отрицательные, либо седлами в случае . В системе возможны два типа бифуркаций. Во-первых, переход фокус — узел прии, во-вторых, переход узел — седло при .Рассмотрим эти возможности. Для точки, так что для любыхвыполняется условие,и точки являются седлами.

Для точки . При , так что особая точка — устойчивый фокус, так как .При ,и точка превращается в устойчивый узел. При, так что , и устойчивый узел переходит в седло.

Таким образом, по мере увеличения угловой скорости вращения затухающие малые колебания в окрестности точки переходят в апериодические, а затем точка становится неустойчивой. Бифуркация присопровождается появлением пары устойчивых точек при, как было показано ранее для случая:

.

При

,,,

т. е. появившиеся особые точки — устойчивые узлы, движение вблизи которых—апериодические колебания. При и происходит бифуркация, превращающая эти точки в устойчивые фокусы. Процесс перестройки фазовой плоскости можно изобразить на диаграмме, показывающей характер и положение особых точек в зависимости от параметра (рис. 11.15). Здесь сплошной толстой линией отмечены устойчивые фокусы, точками — устойчивые узлы, а сплошной тонкой линией — седловые точки. Характер бифуркации на фазовой плоскости вблизи точкиизображен на рис. 12.15. В этом случае из устойчивого узла припоявляется седло прии пара устойчивых узлов в точках.На рисунке изображена окрестность точки. Общая структура фазовой плоскости и характер кривых в случаеиизображены на рис. 13.15.

Характер бифуркаций, рассмотренных выше, весьма разнообразен, однако существуют некоторые правила, запрещающие произвольное рождение или уничтожение особых точек. Отбор возможных бифуркаций можно провести, вводя индекс Пуанкаре. Пусть на фазовой плоскости имеется произвольный замкнутый контур Г без самопересечений, не проходящий через особые точки, и в некоторой его точкеопределен вектор фазовой скорости. При обходе контура векторы фазовой скорости, определенные на этом контуре, будут поворачиваться и, совершив некоторое целое число оборотов ,вернутся в исходное положение в точке.Если определить угол между векторами фазовой скорости и каким-либо постоянным направлением, например осью, то угол изменится на величину. Число оборотов, совершенных вектором при обходе контура, называется индексом замкнутого контура Г.

Если система динамических уравнений исследуемой задачи имеет вид

,

то, поскольку , индекс контура определяется интегралом:

.

Очевидно, что если всюду в области, охватываемой контуром, подынтегральная функция и ее производные непрерывны, то .В особых точках ,так что знаменатель дроби обращается в нуль, что может вести к нарушениям непрерывности. Для того чтобы исключить особые точки, необходимо рассматривать многосвязную область (рис. 14.15).

Таким образом, для определения индекса кривой необходимо выписать сумму индексов кривых ,охватывающих особые точки. Поскольку кривую можно расположить в непосредственной близости от особой точки, то при вычислении интеграла можно ограничиться линейным приближением для функций и. Полагая

где ,—координаты особой точки, выберем в качестве контура интегрирования эллипс

.

Тогда знаменатель подынтегрального выражения обращается в единицу, и интеграл имеет вид

,

но , где —площадь эллипса;, а коэффициенты разложения определяют знаки корней характеристического уравнения

,

так что

.

Это приводит к выражению для индекса Пуанкаре

.

Отсюда получаем индексы кривых, охватывающих особые точки. Для центра и фокуса , так что и . Для узлаи оба корня отрицательны, так что, т. е. .Для седловой точки ,а, что приводит к значению . Обход регулярной точки не поворачивает вектор фазовой скорости.

Таблица индексов Пуанкаре
Тип особенности	Центр	Фокус	Узел	Седло	Регулярная точка
Индекс Пуанкаре	-1	+1	-1	-1	0

Если на фазовой плоскости имеется замкнутая интегральная кривая, например предельный цикл, то, поскольку вектор фазовой скорости на такой кривой касателен к ней, он поворачивается на угол при полном обходе контура. Таким образом, внутри замкнутой интегральной кривой должна находиться хотя бы одна особая точка, имеющая индекс .Если в контуре имеется несколько особых точек, то количество седел на единицу меньше, чем других особых точек.

Более подробно изложение этого вопроса см. в книге Боголюбов Н. Н., Митропольский Ю. А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974.