15.2. Автономные системы

Качественное исследование динамической системы в общем случае очень сложно, поэтому мы рассмотрим некоторые частные случаи, часто встречающиеся в задачах механики. Если правые части дифференциальных уравнений 1(1.15) не зависят явно от времени, то система называется автономной. Векторное поле автономной системы является стационарным. Фазовые траектории системы касаются соответствующих векторов и, следовательно, также являются стационарными. Поскольку фазовые траектории не меняются с речением времени, для решения этих уравнений справедливо следующее утверждение.

Если —решение автономной системы, удовлетворяющее начальным условиям ,то также является решением автономной системы, проходящим через оказанную точку. Таким образом, две различные фазовые траектории автономной системы не пересекаются. Действительно, если предположить, что два различных решения и проходят через одну точку , то в силу сделанного утверждения эти решения совпадают при всех. Фазовая траектория автономной системы, имеющая точку самопересечения, или состоит из одной точки, или является периодической с некоторым периодом. Действительно, если при некотором

,

то решения совпадают при всех t.В этом случае имеются лишь две возможности выбора:

если равенство справедливо при любых , то, полагая, получим , т. е. траектория системы — точка;

если равенство выполняется не при любых , то существует минимальное значение(—период), такое, что .

Таким образом, мы приходим к выводу, что любая траектория автономной системы принадлежит к одному из трех типов:

траектория без самопересечений;

замкнутая траектория, называемая циклом;

траектория, состоящая из одной точки.

Траектории, состоящие из одной точки, называют точками покоя. Эти траектории определяют положения равновесия системы. Необходимым и достаточным условием того, что точка фазового пространства является точкой покоя, будет выполнение условия ,т. е. фазовая скорость системы в точке покоя равна нулю.

Исследование движения автономной системы вблизи точки покоя во многих случаях можно провести в линейном приближении, разложив в ряд функции в окрестности рассматриваемой точки и ограничиваясь линейными членами

.

В этом случае система динамических уравнений в окрестности точки покоя заменяется линейной однородной системой с постоянными коэффициентами

.

Предположим, что

.

Для пространства с одной степенью свободы фазовое пространство двумерно и в окрестности изолированных точек покоя является плоскостью.

Если матрица диагонализована, то уравнение (1.15) можно привести к виду

,.

Решения уравнений имеют вид

,.

Если при этом окажется, что ,то при фазовые траектории стремятся к точке покоя. Система фазовых траекторий, подходя к точке покоя, образует «устойчивый узел», изображенный на рис. 1.15,а.

Если выполнены неравенства ,то форма траекторий остается такой же, но движение точки в этом случае происходит от точки покоя. Такая система траекторий образует неустойчивый узел.

Пусть иимеют противоположные знаки:,. возникающая картина фазовых траекторий — «седло» — имеет две траектории, асимптотически приближающиеся к точке покоя, — «устойчивые усы», и две траектории, выходящие из этой очки, — «неустойчивые усы». Остальные траектории асимптотически приближаются к осям координат, как показано на рис. 1.15,б.

1 Если матрица не приведена к диагональному виду, то апологическая структура фазовых кривых в окрестности точек покоя не меняется. Положение «усов» в этом случае определяется собственными векторами, для которых найдены собственные значения матрицы.

В случае, когда собственные значения комплексны, имеются следующие возможности:

| 1) .Решение системы имеет вид

,.

Фазовые траектории для этого случая — эллипсы. Такая система называется центром (рис. 1.15, в).

2) .В этом случае система фазовых кривых называется устойчивым фокусом. Закон движения в этом случае имеет вид

,

Логарифмические спирали фазовых траекторий в этом случае асимптотически приближаются к точке покоя.

3) .Такая система называется неустойчивым фокусом. Вид кривых на фазовой плоскости такой же, как в предыдущем случае, но точки удаляются от положения равновесия. Отметим, что для всех рассмотренных случаев, кроме случая ,малое изменение параметров системы, а следовательно, и матрицы не меняет качественного характера движения вблизи точки покоя. Небольшие изменения параметров системы для случая превращают центр в устойчивый или неустойчивый фокус.

В случае кратных корней возможны следующие ситуации. Если матрица диагонализуема и, то решение уравнений имеет вид ,, так что.Фазовые траектории такой системы — прямые, проходящие через точку покоя. Такая система фазовых траекторий называется устойчивым дикритическим узлом. Если в этом случае, то получается система, называемая неустойчивым дикритическим узлом, изображенным на рис. 1.15,д. Если матрица имеет вид

,

то решение системы в этом случае представляется в виде

,.

При уравнения определяют системы фазовых траектории, стремящихся к точке покоя — вырожденный устойчивый узел (рис. 1.15,е). Прифазовые траектории выходят из точки покоя. Такая система называется неустойчивым вырожденным узлом.

Если ,то возможна ситуация, когда.В этом случае фазовые траектории — прямые, параллельные оси ординат. При траектории параллельны оси абсцисс.

Мы привели классификацию точек равновесия и рассмотрели характер движения системы в окрестности этих точек в линейном приближении. Очевидно, что этим не исчерпываются все возможные случаи. Детальный анализ различных случаев приведен в математической литературе^.

Для физических приложений наибольший интерес представляют точки устойчивого равновесия, поскольку фазовые траектории «притягиваются» к этим точкам. Множества, к которым притягиваются фазовые траектории динамической системы, называются аттракторами. Области фазового пространства, через которые проходят фазовые траектории, притягивающиеся к аттракторам, называются бассейном аттрактора.

Для изучения свойств предельных множеств, к которым стремятся фазовые траектории, удобно использовать понятие об инвариантных множествах операторов. Назовем инвариантным множеством оператора такое подмножество точек фазовой плоскости, которое переходит в себя под действием этого оператора. Если оператор— оператор эволюции динамической системы, то неподвижные точки этого оператора представляют пример инвариантного множества.

Другим примером инвариантных множеств оператора эволюции автономной области являются сепаратрисные кривые, начинающиеся или заканчивающиеся в седловых точках. Эти кривые разделяют фазовую плоскость на области, движение в которых имеет качественно различный характер.

Существует еще один тип инвариантного множества оператора эволюции автономной системы — изолированный предельный цикл, введенный А. Пуанкаре. Если динамическая система Описывается дифференциальными уравнениями, то предельным циклом называют изолированное периодическое решение. Решение уравнений называют изолированным периодическим решением, если решения, проходящие через любую сколь угодно близкую к предельному циклу точку, не является периодическими. Иными словами, в любой -окрестности предельного цикла нет других замкнутых траекторий. Предельный цикл разбивает фазовую траекторию на две области: внешнюю и внутреннюю. Поскольку фазовые траектории автономной системы не могут пересекаться, любая траектория, отличная от предельного цикла, является либо внешней, либо внутренней. Предельный Цикл называется устойчивым, если все траектории, и внешние И внутренние, начинающиеся в е-окрестности цикла, приближаются к нему. Если все траектории из рассматриваемой области удаляются от предельного цикла, то он называется неустойчивым. Если некоторые траектории, например внешние, приближаются к предельному циклу, а другие, например внутренние, удаляются от этого цикла, то цикл называется полуустойчивым. Кроме рассмотренных фазовых траекторий, в-окрестности предельного цикла других траекторий не существует. Покажем это, используя метод, разработанный и использованный для анализа динамических систем А. Пуанкаре, — метод точечных отображений.

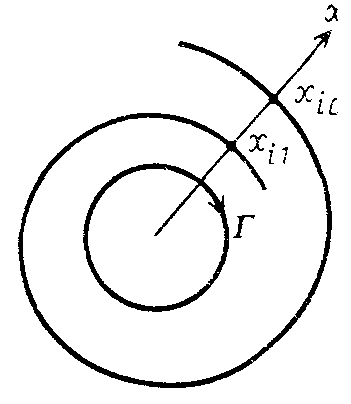
Пусть Г — замкнутая траектория предельного цикла, a G — некоторая траектория, порождаемая уравнениями движения вблизи предельного цикла. Пусть в некоторый момент движение по кривой начинается из точкина рис. 2.15. Проведем отрезокАВ,пересекающий кривую Г. Поскольку точкумы выбираем близкой к предельному циклу, то в течение некоторого времени траектория будет оставаться в окрестности цикла. Предположим, что траектория приближается к Г. Тогда в некоторой точкеона пересечет отрезокАВ.Введем координатувдоль отрезка с началом в точке.Функция, сопоставляющая каждой точке отрезкакоординату точки пересечения траектории после одного оборота, называется функцией последования

.

Рис. 2.15

Отметим некоторые важнейшие свойства этой функции для автономных систем.

Так как через каждую точку фазовой плоскости автономной системы проходит лишь одна фазовая кривая, функция исследования имеет обратную, причем обе функции являются непрерывными.

Покажем, что функция последования является монотонной Пусть координата неподвижной точки на осиравна. Очевидно, что—корень уравнения.Так как мы рассматриваем изолированное решение, в рассматриваемой окрестности других корней нет, поэтому для всех точек выполняется только неравенство или только неравенство, что и доказывает наше утверждение.

Любая траектория, проходящая через некоторую точку , образует последовательность, где, которая является монотонной и ограниченной. Следовательно, она имеет предел, единственный и совпадающий с.Поскольку для достижения предельного цикла необходимо совершить бесконечно много оборотов, время достижения предельного цикла бесконечно.

Поведение точечного отображения, порождаемого функцией последования, удобно исследовать графически. Для рассмотренного нами случая монотонная функция последования, удовлетворяющая условию изображена на рис. 3.15,а.

Рис 3.15.

Для .быстрого определения характера отображения удобно провести биссектрису .Тогда последовательность отображений образует «лестницу» — лестницу Ламерея. Очевидно, что последовательность сходится к точке:

.

Если выполняется неравенство, то последовательность является расходящейся, как на рис. 3.15,б.

Если графики функций и пересекаются в точке, то малое изменение динамических уравнений, описываемое изменением некоторого параметра системы,мало меняет траектории. В этом случае точкаостается единственным корнем, т. е. предельная точка существует и устойчива относительно малых возмущений системы. Если же функция последования касается биссектрисы угла при некотором значении параметра уравнений, то цикл будет полуустойчивым. В этом случае при точка приближается к,а при удаляется от нее.При изменении параметракривая может пересечь биссектрису, например при.В первом случае мы будем иметь два корня в некоторой области, т. е. два предельных цикла, а во втором случае предельный цикл отсутствует вовсе. Возмущение системы в этом случае может привести к рождению предельных циклов, причем, как следует из приведенных рассуждений, предельные циклы рождаются парами.

Рассмотрим в качестве примера систему особых точек и особых кривых фазовой плоскости математического маятника. Пусть — угол отклонения маятника от вертикали,— параметр затухания, а—параметр осцилляций. Пусть для простоты. Уравнение движения имеет вид

(2.15)

Введем фазовое пространство с помощью переменных ,. Движение в этих переменных описывается системой

(3.15)

Точки равновесия системы определяются условием

,,

откуда ,…

Для определения характера точек линеаризуем систему (3.15)в окрестности точек покоя:

а) в окрестности точек ,;

б) вблизи .

В переменных — отклонения от положения равновесия — система (3.15) имеет вид

где знаки «±» относятся к первому и второму случаям соответственно. Характеристическое уравнение дает для первого случая

,

так что точка покоя здесь — устойчивый фокус, поскольку мы ограничились случаем . Приэти точки — центры. Во втором случае

,

так что ,и точка покоя — седло. Решение уравнений (4.15) в окрестности особых точек имеет вид

.

Собственные векторы, соответствующие значениям , определяют положение сепаратрис: .

При в отсутствие затухания сепаратрисы начинаются в одном седле, а заканчиваются в другом, соседнем, так что плоскость вблизи оси абсцисс оказывается разделенной на ряд изолированных областей, внутри каждой из которых находится особая точка — центр. Поскольку фазовые кривые не могут пересекаться, любая точка внутри ограниченной области никогда не сможет ее покинуть. Так как в центре области находится точка покоя, движение может быть циклом, заключающим эту точку. Этот случай описывает свободные колебания маятника без трения. Если начальные условия выбраны так, что изображающая точка попадает в область, внешнюю по отношению к сепаратрисе, то фазовые кривые здесь начинаются и заканчиваются на бесконечности, так как точек покоя в этой области нет. Этот случай соответствует вращению маятника. Структура плоскости изображена на рис. 4.15.

В случае затухающего маятника картина резко меняется. Вместо центра возникает устойчивый фокус. Сепаратрисы седел идут в фокусы или фазовые траектории из бесконечности попадают в седло. Траектории, начавшиеся вдали от фокусов, обязательно попадут в окрестности этих точек, и маятник будет совершать затухающие колебания через некоторое достаточно большое время при любом выборе начальных параметров. Структура плоскости представлена рис. 5.15.

Рис. 5.15