, . Мы воспользовались очевидным соотношением
.
Учитывая,
что 
,
найдем
,
откуда следует, что если
,
то и
.
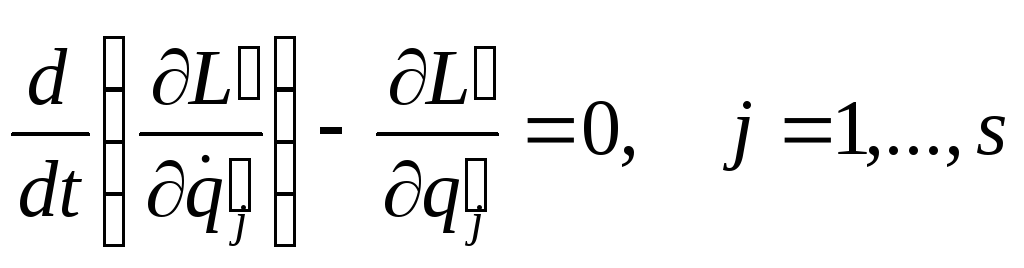Ранее
уравнения Лагранжа в обобщенных
координатах были выведены из принципа
Д’Аламбера
или, как его также называют, динамического
принципа виртуальных перемещений,
который является дифференциальным
принципом в том смысле, что в нем
представлено суждение о движении системы
в каждый момент времени 
.
Можно
показать, что между принципом Д’Аламбера
и принципом наименьшего действия,
который является интегральным принципом,
существует однозначная связь.
Покажем
это на примере консервативных систем.
Динамический принцип виртуальных
перемещений утверждает, что в каждый
момент времени 
должно выполняться равенство
.
Умножим
его на 
и проинтегрируем по 
от 
до 
.
Тогда, если 
,
мы получим
.
А это и есть принцип наименьшего действия.
1Заданные силы
,
часто называют активным силами; силы
же реакции связей
называют пассивными силами.
2Буква, взятая в круглые скобки, обозначает
всю совокупность соответствующих
переменных, например
.
Иногда с целью упрощения записи, там,
где это понятно, круглые скобки не
ставятся.
3См., например:ОльховскийИ. И. Курс теоретической механики, для физиков. Изд-во МГУ, 1974.
4Заметим, что точечные преобразования независимых координат, в формулы которых явно входит время, можно рассматривать как преобразования между координатами в различных системах отсчета: в том числе и неинерциальных. Поэтому уравнения движения материальной точки относительно неинерциальной системы отсчета можно записать в форме уравнений Лагранжа.