7.8. Обобщенный импульс, обобщенная энергия

При наличии обобщенно-потенциальных и диссипативных сил уравнения Лагранжа можно записать в виде

, (52.7)

где - обобщенно - диссипативные силы.

Рассмотрим систему из точек, находящуюся в поле потенциальных сил. Функцию Лагранжа этой системы запишем, выбирая в качестве обобщенных координат декартовы координаты

.

Вычислим частные производные

и т. д.

Здесь x-, y-, z- компоненты импульса -й частицы соответственно. Основываясь на этих соотношениях, можно ввести понятие обобщенного импульса как величины, равной . Каждой обобщенной координате соответствует обобщённый импульс также называют каноническим импульсом. Запишем (52.7) в форме

. (53.7)

Из (53.7) следует

Теорема. Если от какой-либо обобщенной координаты функция Лагранжа механической системы не зависит, а обобщённая сила , то обобщенный импульс является интегралом движения (т. е. сохраняется). Координата в этом случае называется циклической.

Доказательство теоремы тривиально. В самом деле, если условия теоремы выполнены, то

и .

Обобщенный импульс является, очевидно, линейной неоднородной формой обобщенных скоростей. Действительно,

.

Динамические уравнения (52.7) позволяют ввести понятие ещё одной важной физической величины - обобщенную энергию механической системы. Умножим обе части каждого из уравнений (52.7) на соответствующую скорость и после этого сложим все уравнения:

. (54.7)

Представим в виде

и подставим результат в (54.7)

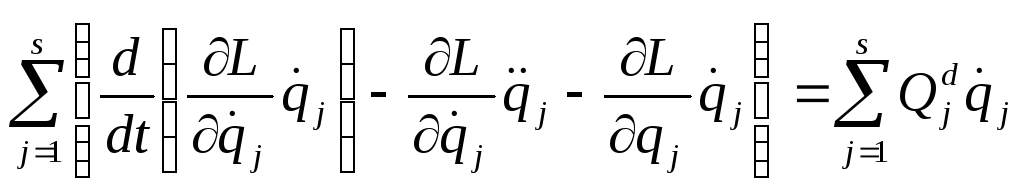. (55.7)

Далее, используя

,

запишем (62.7) в виде

. (56.7)

Функция

(57.7)

является функцией обобщенных координат, обобщенных скоростей и, вообще говоря, времени. Она называется обобщенной энергией механической системы. Из (56.7) следует

Теорема. Если функция Лагранжа механической системы явно от времени не зависит, а диссипативные силы, отсутствуют то обобщенная энергия является интегралом движения.

Действительно, при этих условиях из (56.7) получаем

. (58.7)

Заметим, что условия существования законов сохранения механической и обобщенной энергии в общем случае не совпадают. Так, для сохранения необходимо, чтобы связи были бы стационарными: . Условия сохранения менее жесткие. Таким образом, обобщенная энергия является фактически еще одним интегралом движения (при выполнении условий теоремы), который может быть использован при решении конкретных задач.

Чтобы лучше понять различие между и , установим структуру . Согласно (51.7) и (59.7) имеем

(59.7)

Сравнивая (51.7) с (59.7), видим, что и совпадают только в том случае, если , т. е. при условии, что все . Эти условия выполняются, если все связи, наложенные на систему, стационарны.

Пример. Функция Лагранжа вращающейся рамки. Система, изображенная на рис. 1.7, вращается с постоянной угловой скоростью вокруг вертикальной оси; нижняя точка рамки может двигаться только вдоль вертикальной оси Напряженность поля тяжести равна .ее стержни жесткие и невесомые, Уравнения связей:

Рис. 1.7

Число независимых координат равно единице, так как при равно 1. В качестве независимой (обобщенном) координаты выберем угол . Нетрудно проверить, что тогда

и уравнения связей удовлетворяются тождественно. Выразим через обобщенную координату и обобщенную скорость

.

Найдем функцию Лагранжа

Так как , сохраняется обобщенная энергия

.

Функцию получим из формулы

Равенство представляет собой первый интеграл движения.

В данном примере имеет смысл механической энергии точек в системе отсчета , жестко связанной с рамкой. Чтобы показать это, помимо системы отсчета с неподвижными ортами введем систему отсчета , орт которой направим по оси вращения, орт - в плоскости, а орт - перпендикулярно плоскости рамки. Часть потенциальной энергии систем точек, которая связана с силами инерции, в неинерциальной системе отсчета , движение которой относительно инерциальной системы отсчета задано с помощью функций времени - - ускорения начала системы и -угловой скорости вращения определяется формулой³

.

Здесь - радиус-вектор центра масс в -радиус-вектор -й точки в . В рассматриваемом нами случае

,

поэтому . Эта часть потенциальной энергии определяет центробежные силы, действующие на точки в . Заметим, что добавляется к потенциальной энергии частиц, обусловленной действием внешних сил и силами взаимодействия точек системы.

Пример. Заряженная частица в электромагнитном поле. Построить лагранжиан заряда массы в электромагнитном поле, описываемом скалярным и векторным потенциалами. Найти обобщенную энергию. Показать, что уравнения Лагранжа имеют вид

,

где - напряженности электрического и магнитного полей соответственно.

В качестве обобщенных координат будем использовать декартовы координаты . Тогда

,

а функция Лагранжа

.

Из (66.7) следует, что обобщенная энергия заряда в данном случае

имеет смысл механической энергии заряда. Очевидно, можно также записать в виде

.

Уравнение Лагранжа в векторной форме

,

или

.

Здесь учтено, что . Выше было показано, что (см. (40.7) - (44.7))

,

и, значит, уравнения Лагранжа приобретают вид

.

В частности, если поля однородны и постоянны, то векторный и скалярный потенциалы можно, например, задать как

,

где и - постоянные векторы, не зависящие от координат.