2.3. Прямая и обратная (основная) задачи механики

Второй закон Ньютона (2.2), или, что то же самое, векторное уравнение движения, представляет собой три дифференциальных уравнения второго порядка по времени. Например, проектируя обе части (2.2) на оси декартовой системы координат, получим

(9.2)

Различают две задачи динамики: 1) по заданному закону движения точки, т. е. по известному как функция векторному соотношению находят силу , действующую на точку; это прямая задача динамики

2) по заданной силе находят закон движения точки ; это обратная (основная) задача динамики. Поговорим об основной задаче динамики более подробно. Для ее решения недостаточно знать только силу. Следует задать также механическое состояние в некоторый момент времени , т. е. начальные условия . Механическое состояние точки в момент , т. е. однозначно определяется ее начальным механическим состоянием и условиями ее движения (уравнениями движения). Это следует из однозначности и единственности решения дифференциальных уравнений (2.2), удовлетворяющих данным начальным условиям. Сформулированное предложение о предсказуемости эволюции механической системы во времени при заданных начальном состоянии и условиях движения называется принципом механической причинности, или принципом механического детерминизма. Его суть наиболее точно и полно выразил Лаплас: «Разумное существо, которое в каждый момент знало бы все движущие силы природы и имело бы полную картину состояния, в котором природа находится, могло бы (если бы только его ум был в состоянии проанализировать эти данные) выразить одним уравнением как движение мельчайших атомов, так и движение самых больших тел мира. Ничто не осталось бы для него неизвестным, и оно могло бы обозреть одним взглядом как будущее, так и прошлое», т. е. по начальным состояниям и взаимодействиям состояние системы в любой момент времени в будущем определялось бы однозначно. Со времен Лапласа появились новые важные идеи. Вот одна из них.

Хотя уравнения, описывающие эволюцию механической системы во времени, вполне детерминированы, ее развитие во времени может различаться своими маршрутами. Это связано с чувствительностью некоторых систем к начальным условиям, а точнее, к даже малому изменению начального состояния. В классической динамике в качестве примера можно привести шарик, падающий на острие лезвия бритвы, траектория которого после соприкосновения существенно зависит от положения шарика относительно острия в момент времени перед тем, как он касается лезвия.

Решение уравнения (2.2), которое удовлетворяет какому-либо конкретному начальному условию, называют частным решением. Более важно найти решение, удовлетворяющее произвольным условиям, это так называемое общее решение.

2.4. Интегралы движения

В теории дифференциальных уравнений есть понятие первых интегралов. Первыми интегралами уравнений движения (9.2) будем называть такие функции координат, скоростей и времени, которые обращаются в постоянные в силу этой системы дифференциальных уравнений

. (10.2)

Это означает, что система (9.2) может быть сведена к эквивалентной

. (11.2)

Условие функциональной независимости трех первых интегралов (рассматриваемых как функции скоростей) записывается виде неравенства нулю (функционального) определителя Якоби

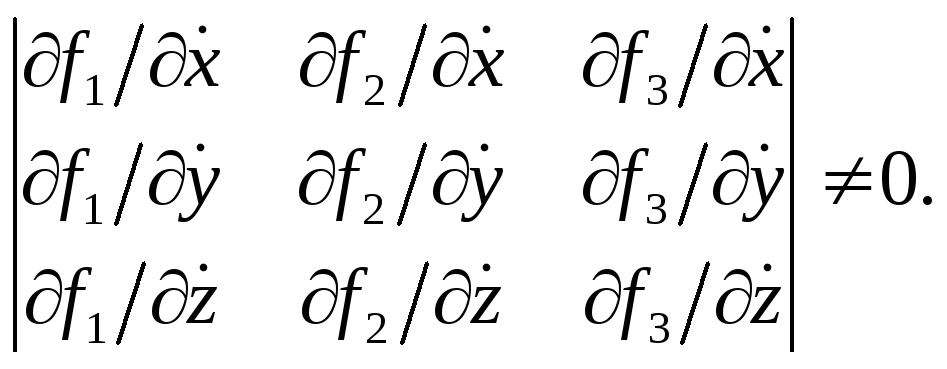(12.2)

Если (12.2) выполнено, то три первых интеграла движения будут независимыми в смысле разрешимости системы конечных уравнений (10.2) относительно . Условие (12.2) является необходимым и достаточным условием независимости первых интегралов движения. Далее, система (10.2) представляет собой систему дифференциальных уравнений 1-го порядка. Предположим, что мы свели ее к эквивалентной системе уравнений

, (13.2)

т. е. мы нашли такие, что

. (14.2)

называют вторыми интегралами движения. Они являются независимыми, если уравнения (14.2) разрешимы относительно координат. Условие независимости - неравенство нулю функционального определителя

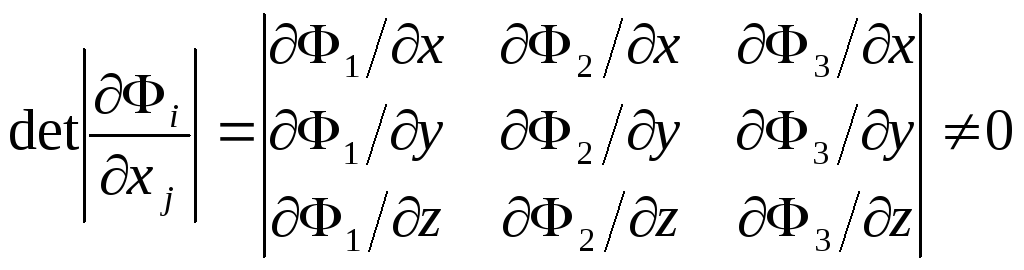. (15.2)

Решение системы (14.2) представляется в виде

(16.2)

Найденные таким образом функции (16.2), являющиеся решением системы уравнений (9.2) и содержащие шесть произвольных постоянных интегрирования, называют общим решением, так как, придавая определенные значения постоянным можно получить функции (10.2) при любых начальных условиях. Выражение постоянных через начальные значения проводится элементарно в два приема.

1. Из системы (10.2) при имеем

(17.2)

2. Подставляя в систему (14.2), взятую при , из (17.2), находим

(18.2)

Найти общее решение уравнений движения - это значит полностью решить обратную задачу динамики.

Пример. Найти общее решение векторного уравнения движения (1.2), если сила зависит только от времени .

Интегрируя (1.2) один раз, получаем три первых независимых интеграла движения

,

где постоянный вектор - это начальная скорость . Интегрируя последнее уравнение, получаем три независимых вторых интеграла движения

.

Здесь . Общее решение имеет вид

.

Пример. Пусть проекции силы в уравнениях (9.2) зависят только от соответствующих координат. Найти все первые интегралы движения в этом случае и общее решение (в квадратурах).

Введем обозначения . Тогда (9.2) можно переписать в виде . Последние уравнения, очевидно, имеют три первых интеграла

.

Откуда находим

.

Знак перед корнем нужно выбирать в соответствии с начальным состоянием. Разделяя переменные и интегрируя, найдем

.