13.5. Геометрическая интерпретация пуансо

Представление о движении вектора угловой скорости твердого тела в случае Эйлера может быть сделано наглядным, если учесть, что в этом случае вектор кинетического момента сохраняется Сохранение направления вектора в пространстве фиксирует плоскость движения Выберем систему координат некоторой инерциальной системы отсчета так, чтобы ортбыл направлен вдоль вектора

.

Проекции вектора на орты системы, связанной с твердым телом, изменяются .Учитывая, что компоненты этого вектора выражаются через компоненты вектора угловой скорости :

,

вычислим скалярное произведение

..

Поскольку энергия в рассматриваемом случае является интегралом, то полученное соотношение означает, что сохраняется проекция вектора угловой скорости на ось

.

Таким образом, концы вектора угловой скорости при движении будут лежать в некоторой плоскости , перпендикулярной вектору кинетического момента, а в нашем случае — оси С другой стороны, сохранение кинетической энергии приводит к тому, что величина вектораменяется, так как геометриче­ское место концов вектора определяет эллипсоид инерции

.

Таким образом, движение вектора угловой скорости при вращении твердого тела происходит так, как будто эллипсоид инерции «катится» без проскальзывания по плоскости .

Совместное выполнение условий движения эллипсоида инерции по плоскости

определяет кривые - точки касания плоскости и эллипсоида инерции. В координатах, связанных с твердым телом, где тензор инерции диагонален (орты), эти уравнения определяют поверхности сферыи эллипсоида инерции:

Пересечение этих поверхностей определяет геометрическое место точек полюсов вектора угловой скорости — полодии. Вводя константы вместоис помощью соотношений

,,

нетрудно показать, что на плоскостях ипроекции линий пересечения образуют семейство эллипсов:

,

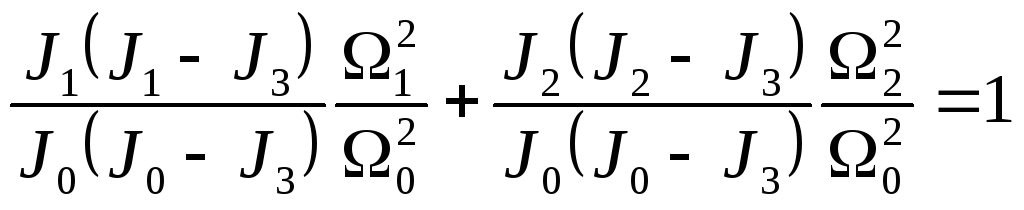а проекция на плоскость определяет семейство гипербол:

.

13.6. Твердое тело во внешнем поле. Случай лагранжа

В случае твердого тела, движущегося в за­данном внешнем поле, переменные разделяются, и решение может быть получено в виде квадратур только в некоторых спе­циальных случаях В случае Лагранжа движение происходит в однородном поле тяжести и предполагается, что вращающееся тело обладает симметрией, так что .Предположим, что в этом случае орты, выбраны так, чтобы они совпадали с главными осями тензора инерции, а лабораторная система ориентирована так, что сила тяжести направлена вдоль осиМы будем предполагать, что твердое тело имеет неподвижную точку, которая находится на расстоянииот центра масс, и выберем начало лабораторной системыО,совпадающим с неподвижной точкой. Положение твердого тела относительно инерциальной лабораторной системымы будем задавать углами Эйлера, как показано на рис 1 13

Для составления уравнений движения твердого тела в этих переменных может быть использован лагранжев подход. Кинетическую энергию вращающегося тела удобно вычислять, используя теорему Кенига. В этом случае функция Лагранжа легко вычисляется:

..

Поскольку функция Лагранжа не зависит явно от углов прецессии и собственного вращения,в системе сохраняются соответствующие обобщенные импульсы:

.

Кроме того, функция Лагранжа не зависит явно от времени, что приводит к сохранению обобщенной энергии, которая в данном случае совпадает с полной:

(41.13)

Поскольку число первых интегралов задачи равно числу независимых координат, возможно провести разделение переменных и получить решение в виде квадратур. Подставляя выражения для обобщенных скоростей в интеграл энергии (41.13), мы приходим к уравнению с разделяющимися переменными

, (42.13)

где —эффективная энергия, определяемая выражением

.

Решение уравнения (42.13) в виде квадратуры получается элементарно:

.

Область возможных значений угла нутации определяется условием. При функцияобращается в бесконечность при, а в интервале между этими значениями имеет минимум. Таким образом, при любыхдвижение происходит в области ,где определяется условием.

В общем случае решение уравнения (42 13) будет весьма громоздким, однако в некоторых частных случаях решение может быть получено в элементарных функциях. В частности, тело может вращаться вокруг вертикальной оси Найдем условия, при которых это вращение существует и устойчиво.

Пусть .При этом ортыисовпадают, так что. Поскольку,

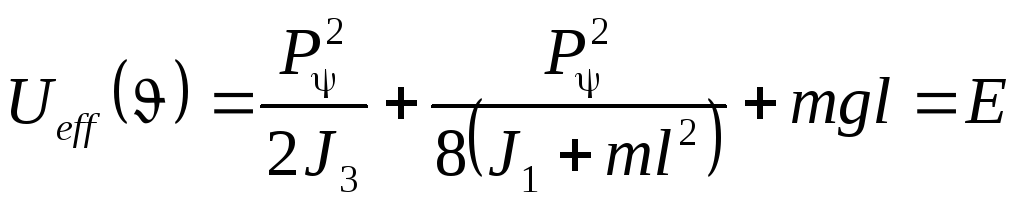. (43.13)

В окрестности точки покоя эффективная потенциальная энергия может быть разложена в ряд по:

.

Функция имеет минимум при в случае

, (44.13)

поэтому при выполнении условия (44.13) движение тела вокруг вертикальной оси устойчиво.

Другой случай — псевдорегулярная прецессия при осуществляется также при достаточно большой скорости вращения тела вокруг оси симметрии Пусть параметры задачи выбраны так, что, а. В этом случае интегралы движения выражаются через заданные значения углов и угловых скоростей:

,.

Эффективная энергия для заданных условий имеет вид

(45.13)

Значение полной энергии, при котором ,

.

Для исследования движения вблизи точки разложимпо степеням, ограничиваясь степенямине выше второй Интеграл энергии имеет вид

Дифференцируя это уравнение по времени, получим линейное уравнение для отклонения от точки покоя:

.

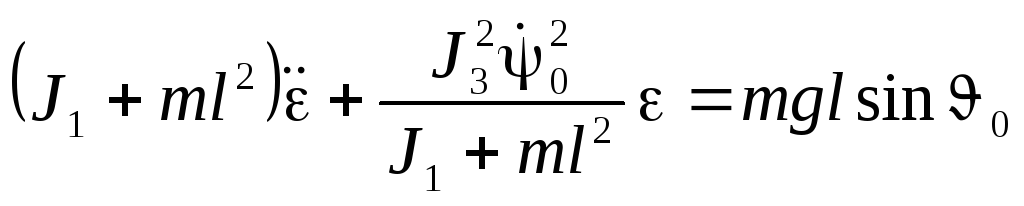Решение этого уравнения при начальных условиях ,имеет вид

, где.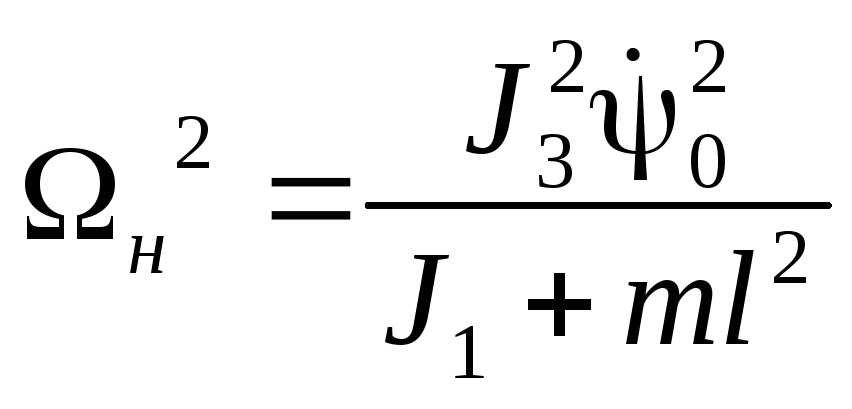

Учитывая полученное выражение, нетрудно получить зависимость углов Эйлера от времени, используя интегралы задачи

,

,

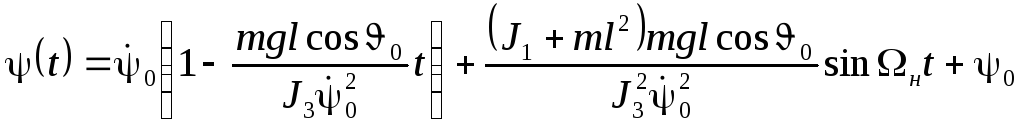. (46.13)

Движение можно рассматривать как медленную прецессию вокруг вертикали. Скорость прецессии тем меньше, чем больше угловая скорость собственного вращения. На это медленное движение накладывается колебание с малой амплитудой и высокой частотой .Одновременно происходят малые колебания угла нутациис частотой.

18