13.4. Свободное движение. Случай эйлера

Рассмотрим подробнее общий случай свободного движения, когда решение может быть получено в квадратурах, — случай Эйлера. В этом случае задача интегрирования может быть разделена на две части. Во-первых, может быть проинтегрирована в квадратурах система динамических уравнений Эйлера и получены выражения для компонент вектора угловой скорости независимо от выбора координат, определяющих ориентацию твердого тела, и, во-вторых, до конца интегрируется система кинематических уравнений, например, при выборе в качестве параметров углов Эйлера. Первая часть задачи решается благодаря выбору подвижной системы координат для записи динамических уравнений, поскольку в этом случае коэффициенты не зависят от времени.

Система однородных уравнений Эйлера имеет два очевидных интеграла — энергию и квадрат кинетического момента:

(31.13)

Используя эти интегралы, легко исключить любые две функции, например и, из уравнений движения. Обычно исключаюти оставляют уравнение для :

.

Полученное уравнение является уравнением с разделяющимися переменными и легко интегрируется. Прежде чем переходить к вычислению квадратуры, проведем качественное исследование и рассмотрим возможные области изменения параметров и переменных. Пусть движение происходит с некоторым заданным значением величины кинетического момента .

Движение возможно лишь в области изменения энергии и переменной , удовлетворяющих условию .Структура уравнения совпадает со структурой уравнения в задаче об одномерном движении в случае существования интеграла энергии. В этом случае полезным оказывается введение эффективной потенциальной энергии, зависящей от дополнительных параметров, определяемых начальными условиями (например, кинетического момента в задаче о движении в центральном поле). В рассмотренных ранее задачах, однако, энергия входила линейно, а в нашем случае выражение

содержит не только линейные, но и квадратичные по энергии члены. Такая структура характерна для релятивистских одномерных задач, где интегралом является квадрат четырехмерного импульса. Полезно поэтому несколько обобщить понятие эффективной энергии, определив ее условием .В нашем случае это приведет к существованию двух ветвей эффективной энергии,определяемых уравнениями

,. (32.13)

Поскольку мы полагаем , введем следующие обозначения:

,.

Значения параметров и определяют область изменения энергии в рассматриваемой задаче при фиксированном значении кинетического момента:

.

Зависимость изображена на рис. 1.13. Движение с заданным значениемпроисходит в области

,

что определяет область изменения переменной :

Границы области, соответствующие значениям ,, определяют точки остановки. В отличие от обычных графиков разность теперь не является кинетической энергией точки, так что непосредственное определение скорости по виду графика несколько сложнее. В рассматриваемом случае,

т. е. определяется средним геометрическим. Максимальное значение достигается в тачках, удовлетворяющих условию.

Подставляя сюда значения из уравне­ний (32.13), получим

,.

Таким образом, при энергии тело вращается вокруг оси, совпадающей с ортом. При ось вращения лежит в плоскости и может занимать любое положение по отношению к ортам. В частности, если ,то,.Таким образом тело, вращающееся вокруг оси с минимальным моментом инерции, обладает максимальной энергией, а точка на графике, изображает это состояние. Соответственно прии ,вращение происходит вокруг оси.

Вблизи границы области движение является равноускоренным, так что граница достигается за конечное время. Действительно, пусть изображающая точка движется вблизи . Разложим в окрестности точки:

,

где

.

В этом случае справедливо приближение

,

т. е.

,

так что интеграл сходится. Этот результат означает, что все точки границы

и

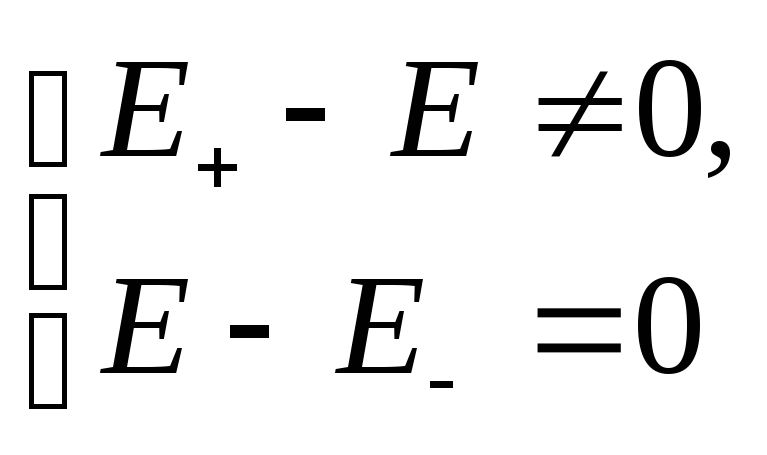
являются точками поворота и достигаются за конечное время. Таким образом, движение изображающей точки — колебания. Угловая скорость при заданном значении моментасовершает колебания, амплитуда которых зависит лишь от значения энергии и определяется условием

.

Кинетическая энергия движения, обусловленного изменением параметра имеет в рассмотренных точках простой корень. Точкииявляются точками устойчивого равновесия, а движение в окрестности этих точек — гармонические колебания.

Несложно вычислить период этих колебаний и определить закон движения. Пусть, например, ,где.Это соответствует вращению вокруг оси. Полагая, что в этом случае

,

получим приближенное уравнение для :

.

Решение этого уравнения дает гармонические колебания для :

,

которые происходят с амплитудой ,определяемой отклонением энергииот экстремума,а частота этих колебаний определяется лишь компонентами тензора инерции и величиной кинетического момента

.

Учитывая связь между компонентами угловой скорости (31.13)

при получим выражения для компонент и

,

.

Таким образом, вектор угловой скорости описывает эллипсы вокруг оси ,причем полуоси этих эллипсов определяются малой амплитудой колебаний. Поскольку величина вектора скорости практически равна ,то период вращения вектора угловой скорости вокруг оси

.

Аналогичные выражения справедливы и для вращения вокруг оси .Выражения для них могут быть получены простой заме­ной индексов:

.

Несколько сложнее исследовать движение в окрестности точки . Приточкаявляется корнем кратности 2 для выражения. В этом случае, как следует из общей теории качественного исследования движения, особая точка не может быть достигнута за конечное время.

Подставляя значение в уравнение для угловой скорости, получим дифференциальное уравнение

где

.

Интегрирование этого уравнения дает

.

Выбирая константу интегрирования так, чтобы

,,

получим явное выражение для :

.

Очевидно, что при,но точка остается недостижимой. Закон движения в этом случае совпадает с законом движения математического маятника при.Более подробно исследовать характер движения при энергии,где ,можно, проведя замену переменных, что сводит эту задачу к задаче о движении математического маятника. Для упрощения обозначений введем вместо константи,определяющих энергию и момент твердого тела, переменные размерности угловой ско­рости и, определяемые следующими уравнениями:

,

, (35.13)

с помощью которых уравнения для угловой скорости можно записать в виде

.

В области изменения параметра Епри заданномМвведенные величины удовлетворяют условиям

(при)

(при)

Вращению вокруг оси соответствует случайи, а движение припроисходит так, что :

Рассмотрим подробнее для определенности случай, когда

,

что соответствует области возможных изменений вектора от вращения вокруг осидо вращения вокруг .

Поскольку в этом случае область изменения ограничена условием, можно ввести переменнуюс помощью следующего уравнения:

Изменению этой переменной в области соответствует изменениево всей возможной области. Для переменнойсправедливо уравнение математического маятника

где

.

Этот случай соответствует вращению математического маятника, определяемого углом . Припериод вращения легко оценить, используя метод сшивания решений. Введем характерную частоту

.

Закон движения для переменной записывается в виде квадратуры

.

Этот интеграл является эллиптическим интегралом первого рода, так что закон движения можно записать в виде

, где.

С помощью полученного выражения можно определить период колебаний угловой скорости для интересующего нас случая . Используя разложение эллиптического интеграла при , получим оценку

.

Этот же результат можно получить непосредственно из квадратуры, используя метод сшивания решений, изложенный в п. 14.2.

Вдали от точек остановки закон движения имеет вид

Соответственно для компонент изависимость от времени дается выражениями

,

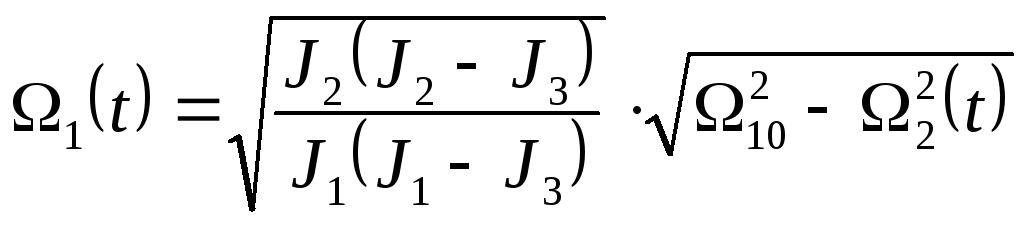(37.13)

Графики зависимости компонент угловой скорости от времени приведены на рис. 2.13.

Рис 2.13

Для определения зависимости углов Эйлера от времени выберем лабораторную систему так, чтобы сохраняющий вектор кинетического момента был направлен вдоль оси OZ: .Учитывая явные выражения для коэффициентов матрицы-

,

,

,

найдем проекции вектора на орты, что сразу же дает явную зависимость углов нутации и собственного вращения от времени:

,.

Угол прецессии определяется из кинематических формул Эйлера квадратурой

. (38.13)