Глава 13. Динамика твердого тела

I 13.1. Общие теоремы динамики в теории твердого тела

Рассматривая твердое тело как систему материальных точек, для описания его движения можно применить теоремы динамики систем со связями. Во многих задачах удобно рассматривать произвольное движение твердого тела как суперпозицию поступательного движения и вращения его вокруг центра масс. Поскольку движение центра масс твердого тела, описываемое теоремой об изменении импульса, ничем не отличается от движения материальной точки, подробно изученного нами ранее, рассмотрим более детально движение твердого тела с одной неподвижной точкой.

Пусть — радиус-вектор точкиm_iтвердого тела. Так как скорость этой точки относительно системы, связанной с твердым телом, равна нулю, то из формулы Эйлера (14.12) следует

, (1.13)

где — угловая скорость тела. Вектор кинетического момента в этом случае определяется формулой

. (2.13)

Для упрощения формул перейдем к тензорной форме записи:

. (3.13)

Подставляя значения координат и проводя суммирование по повторяющемуся индексу m с учетом соотношений (11.12), получим выражение для вектора кинетического момента:

. (4.13)

Величина, стоящая под знаком суммы, является симметричным тензором второго ранга и называется тензором инерции:

(5.13)

Этот тензор характеризует распределение масс твердого тела.

С помощью тензора инерции выражение для кинетического момента представляется в виде

. (6.13)

Теорема об изменении кинетического момента твердого тела, имеющего неподвижную точку, с помощью введенного тензора инерции в лабораторной системе представляется уравнением:

(7.13)

где —момент внешних сил, действующих на тело.

Кинетическая энергия твердого тела в случае вращения с одной неподвижной точкой также может быть представлена с помощью тензора инерции. Действительно, по определению кинетическая энергия твердого тела как системы материальных точек определяется выражением:

. (8.13)

Переходя к тензорным обозначениям, получим выражение для кинетической энергии вращающегося тела, записанное с помощью тензора инерции:

. (9.13)

Поскольку в выбранной модели деформации отсутствуют, то мощность внутренних сил равна нулю, так что изменение кинетической энергии обусловлено лишь внешними силами, действующими на тело:

, (10.13)

где .

В тензорных обозначениях теорема об изменении кинетической энергии твердого тела имеет вид:

. (11.13)

Если среди действующих на тело внешних сил имеются потенциальные, то их действие можно учесть, с помощью потенциальной энергии . В этом случае вместо теоремы об изменении кинетической энергии удобно использовать теорему об изменении полной энергиитвердого тела:

. (12.13)

13.2. Тензор инерции и его свойства

Введенный нами в предыдущем разделе тензор инерции системы точек

для твердого тела, плотность которого , выражается с помощью интеграла

. (13.13)

В лабораторной системе отсчета компоненты тензора инерции являются функциями времени, поскольку распределение масс, характеризуемое координатами точек ,меняется при вращении. Однако в системе отсчета, связанной с твердым телом, эти координаты остаются неизменными, так что компоненты тензора в этой системе — постоянные величины, определяемые лишь распределением масс и не зависящие от каких-либо характеристик движения. Как следует из определения, тензор инерции является симметричным тензором второго ранга, имеющим шесть независимых компонент. Диагональные компоненты тензора называются осевыми моментами инерции, а недиагональные — центробежными моментами инерции.

Соответствующим выбором осей, связанных с твердым телом, можно привести тензор инерции к диагональному виду

, (14.13)

причем в силу положительной определенности кинетической энергии все осевые моменты тензора инерции будут неотрицательны. Диагональные моменты в этом случае называют главными моментами инерции, а соответствующие оси — главными осями инерции. Для определения главных осей инерции необходимо найти такие направления в пространстве, которые не менялись бы под действием матрицы ,т. е. собственные векторы преобразования, определяемого тензором инерции:

, (15.13)

где x_т —компоненты собственного вектора в системе, связанной с твердым телом, —собственные значения. Существование решений системы (15.13), не равных тождественно нулю, возможно при условии

, (16.13)

что определяет три действительных корня — три главных момента инерции.

Введенный тензор инерции связан с моментом инерции тела, вращающегося вокруг заданной оси. Пусть ось вращения тела задана единичным вектором, неизменным по отношению к системе отсчета, так что . Положение оси вращения по отношению к системе, связанной с твердым телом, определяется направляющми косинусамимежду вектороми ортами подвижной системы:

,(17.13)

которые также не изменяются с течением времени. Проекции вектора угловой скорости на орты имеют вид

. (18.13)

Кинетическая энергия тела, вращающегося вокруг фиксированной оси, представляется выражением:

, (19.13)

где скалярная величина

, (20.13)

не зависящая от времени, называется моментом инерции тела. Она определяется распределением масс твердого тела и ориентацией оси вращения .

Этой зависимости можно придать наглядный геометрический смысл, вводя эллипсоид инерции. Рассмотрим вектор, направленный вдоль оси вращения:

.

С помощью этого вектора тензору инерции можно поставить в соответствие скаляр:

.

Поверхность, определяемая условием

, (21.13)

где С– константа, представляет собой трехосный эллипсоид, который называется эллипсоидом инерции. Часто константу выбирают так, чтобы численное значение ее равнялось единице. Если оси, связанные с твердым телом, выбраны так, что тензор инерции в этих осях диагоналей, то эллипсоид инерции определяется соотношением

.

При выборе численного значения константы, равной единице, полуоси эллипсоида инерции а, b, сравны соответственно

,,.

Компоненты тензора инерции любого тела удовлетворяют неравенству треугольника:

,?

и аналогично, для всех других осей.

Действительно,

,

,

,

откуда

,

.

Для системы точек, находящейся в плоскости z= 0, неравенство треугольника переходит в равенство

.

Практически определение главных осей инерции облегчается, если рассматриваемое тело обладает материальной симметрией. Осью материальной симметрииназывают прямую, относительно которой для каждой точки массыm_iможно указать точку такой же массы, расположенную симметрично относительно этой прямой, т. е. отрезок, соединяющий эти точки, проходит через прямую, перпендикулярен ей и делится этой прямой пополам.

Плоскостью материальной симметрииназывают такую плоскость, если для любой точки т, можно указать точку такой же массы, расположенную симметрично относительно этой плоскости, т. е. отрезок, соединяющий эти две точки, перпендикулярен плоскости и делится ею пополам.

Покажем, что центр масс тела лежит на оси материальной симметрии и эта ось является главной осью инерции, т. е. центробежные моменты инерции относительно этой оси равны нулю. Пусть ось OZявляется осью материальной симметрии системы, состоящей из2Nточек, т. е. для каждой точкиm_i, где, задаваемой радиусом-вектором, существует точка массыm_i+N=m_i,положение которой определяется вектором.Положение центра масс системы определяется равенством

,

где - масса системы.

Проводя суммирование получим

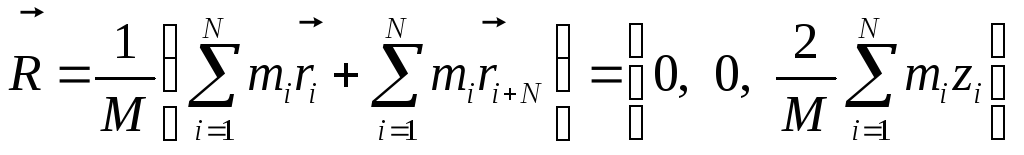
т. е. центр масс находится на оси симметрии.

Центробежные моменты относительно оси OZравны; нулю:

Аналогично .

Центр масс системы точек, обладающей плоскостью симметрии, лежит в этой плоскости, а любая ось, перпендикулярная ей, является главной осью симметрии. Пусть плоскость OXY является плоскостью симметрии рассматриваемой системы2N точек, т. е. для каждой точкиm_i,, определяемой радиусом-вектором,существует точка, масса которойm_i+N=m_i,а радиус-вектор . Очевидно, что , . Поскольку положение начала координат ничем не выделено в плоскостиOXY,то результат справедлив для любой оси, перпендикулярной плоскости, а не только дляOZ.

Для тел, обладающих высокой симметрией, скажем, однородных тел вращения, указанные свойства позволяют сразу же определить главные оси инерции. Так, для тел вращения ось вращения и любые две перпендикулярные ей оси, перпендикулярные между собой, диагонализуют тензор инерции.

Рассмотрим теперь преобразования тензора инерции при сдвиге осей. Пусть в некоторой системе OXYZтензор инерции определяется выражением (5.13). Координаты точек в новой системеO'X'Y'Z',начало которой сдвинуто относительно исходной системы, а оси координат параллельны исходным осям и связаны со старыми соотношением

,

где вектор , определяет сдвиг начала новой системы. Подставляя это выражение в (5.13), получим связь между тензором инерции в исходной системе и в новой :

.

Если начало новой системы совместить с центром масс, то

,

и в этом случае

, (22.13)

где —тензор инерции в системе центра масс, амасса тела.

Параллельный перенос осей преобразует момент инерции системы относительно оси, определяемой вектором :

.

Здесь d=csin a — расстояние от точкиО'системы центра масс до оси вращения, а— момент инерции относительно оси, проходящей через центр масс. Рассмотренное преобразование составляет содержание теоремы Штейнера.