5.3. Полная механическая энергия системы материальных точек

Умножим скалярно (1.5) на ,и просуммируем результат по всем точкам системы:

. (11.5)

Слева стоит дифференциал кинетической энергии системы точек

. (12.5)

Кинетическую энергию

, (13.5)

используя систему отсчета с началом в центре масс (будем называть ее ЦСО), удобно представить в виде

. (14.5)

Таким образом мы показали, что

кинетическая энергия системы материальных точек равна сумме кинетической энергии системы частиц в их движении относительно ЦСО и кинетической энергии «центра масс» т. е. кинетической энергии системы в предположении, что вся масса системы точек сосредоточена в центре масс (теорема Кенига).

Предположим, что внешние и внутренние силы потенциальны и консервативны². Тогда выражение

является полным дифференциалом скалярной функции , имеющей смысл потенциальной энергии системы частиц во внешнем поле. Если, кроме того, удовлетворяют третьему закону Ньютона, то они могут быть построены с помощью некоторой функции

(15.5)

как

. (16.5)

Учитывая, что и ,где f —скалярная функция аргумента, преобразуем двойную сумму:

.

(17.5)

Здесь мы использовали очевидное соотношение

.

Коэффициент 1/2 появился в (17.5), так как при суммировании по i, jкаждый индекс данной пары появляется дважды: при суммировании поiи поj.

Мы видим, что можно определить потенциальную энергию системы точек как

,

и если внешние и внутренние силы консервативны, то, собирая все члены вместе, получим

. (18.5)

Эти равенства выражают собой закон сохранения полной механической энергии системы материальных точек. На их основе можно сформулировать теорему:

Полная механическая энергия консервативной системы материальных точек не изменяется во время движения.

Кратко рассмотрим общий случай, когда внешние силы явно зависят от времени и в системе точек действуют диссипативные силы. Вывод формулы, определяющей скорость изменения полной механической энергии системы точек, подобен выводу аналогичной формулы для одной точки. В результате получим

,

где Еопределяется формулой (18.5), а,- внешние и внутренние диссипативные силы соответственно.

Из формулы (19.5) следует, что полная механическая энергия системы материальных точек сохраняется, если ,а также если, т. е. если убыль энергии за счет диссипативных сил компенсируется поступлением энергии в систему за счет зависящих от времени потенциальных сил.

Для замкнутой системы (в отсутствие также внутренних диссипативных сил) имеем 10 интегралов движения: семь первых (Е=Е₀, ,)и три вторых ().

5.4. Механическое подобие. Теорема вириала

Рассмотрим движение в поле консервативных сил системы точек, потенциальная энергия которой является однородной функцией координат, т. е. функцией, удовлетворяющей условию

,

где — некоторая постоянная, а число  —степень однородности функции. Запишем уравнения движения

(20,5)

и произведем в них преобразование, при котором наряду с изменением всех радиус-векторов в  раз одновременно изменяется враз время:

. (21,5)

Уравнения движения в результате этого преобразования, очевидно, приобретают вид

. (22.5.)

Пусть постоянная связана ссоотношением

. (23.5)

Тогда уравнения движения останутся неизменными. Но радиус-векторы всех частиц мы изменили в раз, т. е. мы сделали переход к геометрически подобным траекториям, которые отличаются от исходных лишь своими линейными размерами. При этом отношение всех времен движения (между соответствующими точками траекторий) равно

. (24.5)

Здесь —отношение линейных размеров двух траекторий.

Рассмотренный переход возможен только в том случае, когда потенциальная энергия системы является однородной функцией v-й степени от декартовых координат. Соотношения типа (24.5) для времен можно получить также и для любых механических величин в соответственных точках траекторий в соответственные моменты времени. Так, для импульсов получим

.

Из формулы (24.5) нетрудно вывести свойство изохронности колебаний математического маятника ( = 2)или третий закон Кеплера ( = - 1).

Докажем теперь теорему вириала для системы материальных точек. Обратим внимание на то, что эта теорема имеет статистический характер. Рассмотрим величину и вычислим

(25.5)

Преобразуем правую часть (25.5):

С учетом этих преобразований имеем

(26.5)

Усредним (26.5) по времени согласно формуле

(27.5)

В результате усреднения получим

.

Для периодического движения справа стоит нуль, так как можно выбрать равным периоду. Аналогично правая сторона обращается в нуль, если координаты и скорость точек системы остаются ограниченными (т. е. не обращаются в бесконечность). Поэтому в любом случае

. (28.5)

Правая часть этого равенства называется вириалом Клаузиуса, а само равенство выражает так называемую теорему вириала В таком виде теорема вириала полезна в кинетической теории газов.

Можно показать, что если в силы будут входить силы трения ,пропорциональные первым степеням скоростей точек, то вириал системы от них зависеть не будет. При этом, разумеется, нужно предположить, что движение системы не прекращается вследствие трения, т. е. в систему поступает энергия на поддержание движения (в противном случае все средние значения будут стремиться прик нулю и равенство (28.5) потеряет смысл).

Рассмотрим случай, когда все силы являются потенциальными. Тогда вместо (28.5) получим

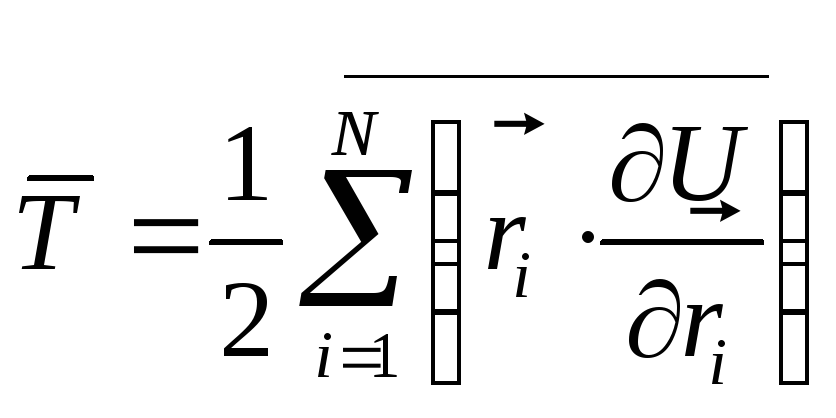. (29.5)

Если к тому же потенциальная энергия является однородной функцией n-й степени от всех радиусов-векторов, то согласно теореме Эйлера об однородных функциях получим

. (30.5).

Теорема вириала. Кинетическая энергия системы материальных точек, усредненная по бесконечному интервалу времени, равна усредненному по тому же интервалу времени вириалу сил.

Так как ,соотношение (30.5) можно представить в формах, полезных для приложений:

. .

Из (30.5) следует, что для гармонического осциллятора (n = 2),для ньютоновского взаимодействия () и.

Теорема вириала используется в классической механике, атомной физике и статистической механике. Ее модификация применяется в квантовой механике.