Правило декомпозиции (разложения)

Правило декомпозиции состоит в том, что если дано X→YZ(значитXсвязан и сYи сZ), тогдаX→YиX→Z. Например:

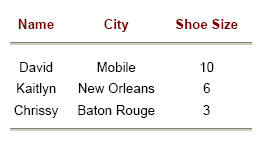
Допустим, есть связь Name → City, ShoeSize. Это значит, что каждому Nameсоответствует уникальное значение City и уникальное значение ShoeSize. Правило гласит, что если от Name зависят City и ShoeSize вместе, то они зависят от Name и по отдельности: Name → City и Name →ShoeSize.

Частичное доказательство с использованием правила рефлексии выглядит так:

Name → City, Shoe Size (дано)

City, Shoe Size → City (по правилу рефлексии)

Name→City(используем шаги 1 и 2 и свойство транзитивности)

Правило объединения

Правило объединения обратно правилу декомпозиции (разложения), оно гласит, что если X → Y и X→ Z, тоX→YZ. В нашем примереName,City, иShoeSizeиллюстрируют это правило. Если мы независимо находим или нам дано, что Name →Cityи дано, чтоName→ShowSize, мы можем немедленно написать, чтоName→City,ShoeSize. (дополнительные доказательства см.ElmasriandNavathe, 2000,p. 480.).

Вы можете не согласиться с этим примером, ведь Nameне является надежным способом определенияCity;Names(имена) могут повторяться. Вы правы,Names(имена) могут не быть уникальными, но обратите внимание на используемый нами язык. В этой базе данных, мыопределяем, зависимостьName(Имя) →City(Город) и, следовательно, в этой базе данных вводим условие, чтоName(Имя) должно быть уникальным.

Ключи и функциональные зависимости

Основная причина определения функциональных зависимостей и логических правил – нахождение ключей и разработка нормальных форм для реляционных баз данных. В любой реляционной таблице, некоторый атрибут(ы) идентифицирует(-ют) остальную часть атрибутов. Атрибут, который идентифицирует все другие атрибуты в строке, называется «потенциальный ключ». «Ключ» означает «уникальный идентификатор» для строки информации. Следовательно, если атрибут или некоторая комбинация атрибутов всегда идентифицирует все другие атрибуты в строке, он(-а) является «потенциальным ключом». Проиллюстрируем на примере:

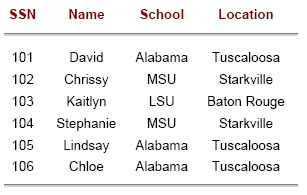
Установим следующие функциональные зависимости:

Хотелось бы, отыскать наименьшее число атрибутов, по которым можно определить все остальные, в идеальном случае – один атрибут. Известно, что SSN похож на потенциальный ключ, но можно ли идентифицировать по SSN все атрибуты? Другими словами, можно ли показать, что SSN определяет все атрибуты в отношении? Известно, что SSN определяет Name(Имя) иSchool(Школу), поскольку это дано. Известно также, что можно вывести следующие транзитивные зависимости:

Поэтому по правилу транзитивности можно сказать, что SSN → Location. Мы вывели три необходимых функциональных зависимости. Используя правило рефлексии, можно затем использовать правило объединения:

SSN → Name (дано)

SSN → School (дано)

SSN→Location(получено, используя правило транзитивности)

SSN→SSN(правило рефлексии (очевидно))

SSN → SSN, Name, School, Location (правило объединения)

Имеется в виду, что, с помощью любого SSN, можно найти уникальное значение каждого поля для этого SSN. Следовательно, SSN является потенциальным ключом для этого отношения. По теории функциональной зависимости (FD), как только мы найдем все функциональные зависимости (FDs), определенные атрибутом, мы обнаружим все связанные с ним атрибуты. В нашем примере, связанными с SSN являются все атрибуты в отношении. Обнаружение потенциального ключа – это обнаружение связанного атрибута или набора атрибутов, которые определяют все другие атрибуты.

Есть ли еще потенциальные ключи? Конечно! Вспомните правило дополнения, в котором говорится, что, поскольку мы определили SSN как ключ, мы можем дополнить SSN и сформировать новые потенциальные ключи: SSN, Name- потенциальный ключ. SSN,Location- потенциальный ключ, и т.п.. Поскольку каждая строка в отношении уникальна, у нас всегда есть, по крайней мере, один потенциальный ключ - набор всех атрибутов.

Является ли Schoolпотенциальным ключом? Нет. Вы имеете одну функциональную зависимость (FD) School →Location, но из нее вы не можете сделать вывод, что School → SSN (к тому же, имеется контрпример, который показывает, чтоSchoolне определяет SSN).

Ключом должен быть минимальный набор атрибутов, который связан со всеми атрибутами в отношении; «минимальный» в том смысле, что с левой стороны функциональной зависимости (LHS FD) будут находиться несколько атрибутов, которые Вы обозначаете как ключ. В нашем примере, SSN будет минимальным (один атрибут) ключом.

Как только мы определили набор потенциальных ключей (или возможно только один как в данном случае), мы определяем один из потенциальных ключей как первичный ключ и переходим к нормальным формам.

Правила функциональной зависимости (FD) полезны и при разработке Нормальных форм. Нормальные формы (NF) могут выражаться различными способами, но использование функциональных зависимостей (FDs) наиболее удобно для иллюстрации этого фундаментального понятия реляционных баз данных. E. Codd (1972) первый определил три нормальных формы: 1NF (1 НФ - Нормальная Форма), 2NF (2НФ), и 3NF (3НФ).