Глава 7: Троичные и er-диаграммы более высокого порядка
Общие представления
Все связи, с которыми мы имели дело в предшествующих главах, были двоичными. Хотя двоичная связь кажется наиболее естественной для нас, в действительности иногда необходимо соединить три или более сущностей. Если связь соединяет три сущности, она называется троичной или "3-ая." Если связь объединяет три или более сущностей (n сущностей), она называется "n-ой" связью, где n – количество сущностей, участвующих в связи. N-ая связь также называется связью более высокого порядка.
В этой главе мы рассмотрим связь, которая соединяет три или больше сущностей. Сначала мы рассмотрим троичную связь (3-ую). Троичная связь возникает по трем главным причинам: (1) если мы имеем пересекающие атрибуты, которым требуется три различных сущности для идентификации, (2) если мы имеем связь для связи, и (3) обратное проектирование. Поскольку обратное проектирование описывается в Главе 9, мы не затрагивать в этой главе установление троичной связи при обратном проектировании.
В этой главе мы сначала обсудим, каким образом пересекающие атрибуты создают троичную связь, затем рассмотрим структурные ограничения на троичныесвязи. Затем мы обсудим, каким образом троичные и другая n-ыесвязи могут быть преобразованы в двоичные связи. Также будет описано возникновение троичной связи вследствие существования связи для связи. Будет пересмотрен Шаг 6 методологии ER-проектирования для того, чтобы учесть троичные исвязиболее высокого порядка.
Двоичная или Троичная связь?
Троичная связьтребуется, когда двоичной связи не достаточно для корректного описания семантики связи между тремя сущностями. В этой части мы объясним различие между двоичной и троичнойсвязьюс помощью примера, а также покажем, как пересекающие атрибуты неизбежно приводят к возникновению троичнойсвязи.
В случае двоичной связи, мы установили, что между сущностями существуютсвязии, что этисвязидолжны иметь структурные ограничения (коэффициент связи и характер участия). Затем мы установили что иногда могут возникать атрибуты связи. В конкретном примере мы выяснили, что связь М:N часто порождает атрибут, который мы назвали пересекающим атрибутом (вспомните связь М:N СТУДЕНТ/КЛАСС и пересекающийся атрибут – оценка, изображенный на Рисунке 6.1). В случае двоичной связи мы отметили, что атрибут оценка подразумевает существование двоичной связь M:N между сущностями. Даже если бы кто-то определил связь M:N, а позже обнаружил «осиротелый» атрибут, который первоначально не был значимым, конечным результатом стала бы связь M:N с пересекающимся атрибутом.
В базах данных возникают случаи, когда необходима связь более, чем между двумя сущностями. В этом случае обычно находится один атрибутов, который приводит к возникновению n-ой связи. Рассмотрим следующий пример.
Пусть имеется база данных компании, которая содержит сущности ПРОДУКТ, ПОСТАВЩИК, и КЛИЕНТ. Обычной связью могла бы стать связь ПРОДУКТ/ПОСТАВЩИК, где компания покупает продукты у поставщика – то есть обычная двоичная связь. Пересекающим атрибутом для связи ПРОДУКТ/ПОСТАВЩИК будет являться оптовая цена (как показано на Рисунке 7.1A). Теперь рассмотрим сущность КЛИЕНТ и предположим, что клиент покупает продукты. Если все клиенты платят одну и ту же цену за продукт, независимо от поставщика, то имеем простую двоичную связь между сущностью КЛИЕНТ и сущностью ПРОДУКТ. Для связи КЛИЕНТ/ПРОДУКТ пересекаемым атрибутом является розничная цена (как показано на Рисунке 7.1B).
Рисунок 7.1A: Двоичная связь ПРОДУКТ и ПОСТАВЩИК и атрибут пересечения – оптовая цена
Рисунок 7.1B: Двоичная связь ПРОДУКТ и КЛИЕНТ и атрибут пересечения, розничная цена
Пример данных для Рисунка 7.1A:
Пример данных для Рисунка 7.1B:
Теперь рассмотрим другой сценарий. Предположим, что клиент покупает продукты, но цена зависит не только от продукта, но также и от поставщика. Предположим, что необходимо знать номер_клиента, номер_продукта и номер_поставщика для идентификации цены. То есть у нас есть атрибут, который зависит от трех сущностей и, следовательно, возникает связь между тремя сущностями (троичная связь), которая будет иметь атрибут пересечения оптовая_цена. Эта ситуация изображена на Рисунке 7.2.
Рисунок 7.2 представляет сущности ПРОДУКТ, ПОСТАВЩИК, КЛИЕНТ и связь покупает между тремя сущностями, изображенную одинарном ромбе.
Примером данных для Рисунка 7.2 может являться таблица:
Рисунок 7.2: ER диаграмма (только с первичными ключами), иллюстрирующая троичную связь
Этот случай троичной связи наиболее реалистичен, поскольку клиенты обычно платят разные цены за один и тот же продукт различных производителей или поставщиков. У разных поставщиков могут быть разные цены на один продукт в различные периоды времени. Также, для клиентов можно допустить, что некоторые товары были куплены на распродаже, а некоторые нет. Еще одним атрибутом пересечения (смотри Рисунок 7.2) могла бы стать дата продажи продукта клиенту поставщиком.
В случае связей более высокого порядка, они чаще всего выявляются нахождением атрибута, который требует существование n-ой связи. Далее мы рассмотрим структурные ограничения на троичные связи.
Структурные ограничения на троичные связи
Троичные связи могут иметь следующие типы структурных ограничений:
один-к-одному-к-одному (one-to-one-to-one) (1:1:1), один-к-одному-ко-многим (one-to-one-to-many) (1:1:M), один-ко-многим-ко-многим (one-to-many-tomany) (1:M:M), и многие-ко-многим-ко-многим (many-to-many-many) (M:M:M), с полным или частичным участием с каждой стороны. Ниже приводится пример связи (M:M:M) с частичным участием со всех сторон:
Структурное ограничение
Многие-ко-многим-ко-многим (M:M:M)
На Рисунке 7A изображен пример связи M:M:N между тремя сущностями: ПРОДУКТ, ПОСТАВЩИК, и КЛИЕНТ. Этот рисунок показывает, что много клиентов могут купить много продуктов у многих поставщиков, по разным ценам.
Рисунок 7A: ER диаграмма, показывающая троичную связь многие-ко-многим-ко-многим
(частичное участие со всех сторон)
Объекты, участвующие в такой связи, приводятся на Рисунке 7B.
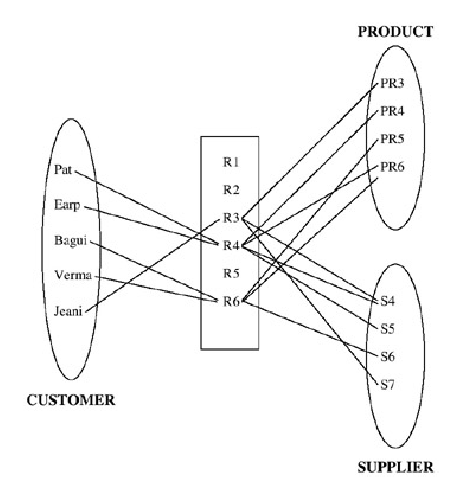
Рисунок 7B: Примеры троичной связи многие-ко-многим-ко-многим для
КЛИЕНТ:ПРОДУКТ:ПОСТАВЩИК
Контрольные вопросы 7.1
1. Что такое троичная связь?
2. Что такое n-ая связь?
3. Что такое связь более высокого порядка?
4. Используя три сущности (ПРОДУКТ, ПОСТАВЩИК, и КЛИЕНТ), нарисуйте ER диаграмму, которая изображает следующее: клиент должен купить один и только один продукт у поставщика по конкретной цене в назначенную дату.
5. Используя три сущности (ПРОДУКТ, ПОСТАВЩИК, и КЛИЕНТ), нарисуйте ER диаграмму, которая изображает следующее: поставщик должен поставить много продуктов многим клиентам по разным ценам за разные даты.
6. Придумайте еще несколько пересекающих атрибутов для сущностей ПРОДУКТ, ПОСТАВЩИК и КЛИЕНТ.
7. Какие ситуации могут создать каждое из следующих структурных ограничений?
ПРОДУКТ: ПОСТАВЩИК: КЛИЕНТ::1:1:1, частичное участие со всех сторон
ПРОДУКТ: ПОСТАВЩИК: КЛИЕНТ::1:M:M, частичное участие со всех сторон
ПРОДУКТ: ПОСТАВЩИК: КЛИЕНТ::1:1:1 полное участие со всех сторон
Пример n-ой связи
N-ая связь описывает объединение n сущностей. В нашем примере троичной связи, мы утверждали, что цена зависит от сущностей ПРОДУКТ, ПОСТАВЩИК, и КЛИЕНТ. Если мы предположим, что цена зависит от сущностей ПРОДУКТ, ПОСТАВЩИК, КЛИЕНТ, а также от ШТАТА,то это означает, что атрибут цена зависит от четырех сущностей, и, следовательно, имеет место n-ая связь (в этом случае, 4-ая). В n-ой связи (или, в этом случае, 4-ой), одинарный ромбсвязи соединяет n (4) сущностей, как показано на Рисунке 7.3.
Рисунок 7.3: ER диаграмма, показывающая n-ую связь
N-ые связи не препятствуют двоичным связям
Наличие троичной связи не означает, что двоичная связь среди сущностей не может существовать. Используя аналогичный пример - ПРОДАВЦЫ, ПОСТАВЩИКИ, и ПРОДУКТЫ, предположим, что розничные продавцы и поставщики продуктов имеют особую связь, которая не касается клиентов, как, например, оптовая торговля с совершенно другой ценовой структурой. Такая двоичная связь может быть изображена отдельно, в дополнение к троичной связи. Рисунок 7.4. иллюстрирует упрощенную версию таких двухсторонних (двоичных) связей и трехсторонних (троичных) связей в ER-диаграмме той же базы данных.
Рисунок 7.4: ER диаграмма (только с первичными ключами), иллюстрирующая трехстороннюю и
двухстороннюю связи
Семантика Рисунка 7.4 сообщает, что имеется двоичная связь, оптовая торговля, между ПРОДУКТОМ и ПОСТАВЩИКОМ, с участием всех ПРОДУКТОВ и ПОСТАВЩИКОВ. Как ПОСТАВЩИК, так и КЛИЕНТ покупают ПРОДУКТЫ, но в связи ПОСТАВЩИК/ПРОДУКТ действием является оптовая покупка и, следовательно, связь помечается как оптовая покупка. Мы изменили название троичной связи на розничная покупка, чтобы можно было различать двоичную связь.
Методология и грамматика для n-ой связи
Нам следует вернуться к шагу 6 методологии ER-проектирования, чтобы учесть вероятность появления n–ой связи. Прежняя версия была:
Шаг 6: Определить на структурированном английском языке точный характер связей с обеих сторон. Например, связь A:B::1:M означает связь A с B вида один-ко-многим с одной стороны и связь B с A вида многие-к-одному с другой стороны.
Добавим следующее предложение к шагу 6:
Для троичных связей и связей более высокого порядка (n-ых) определить все связи на структурированном английском, упомянув все сущности, участвующие в n-ой связи. Указать существующие структурные ограничения.
Грамматика для n-ой связи должна включать все сущности, участвующие в связи и, следовательно, и наиболее общее и простое описание n-ой связи было бы следующим:
СУЩНОСТЬ1 связана с
СУЩНОСТЬЮ2 и с СУЩНОСТЬЮ 3. Очевидно, что требуется называть все n сущностей, чтобы идентифицировать атрибут.
Здесь, если мы выберем некоторую комбинацию Сущность_1,…, Сущность_n, эту приведет к следующему:
Сущность1: КЛИЕНТ
Связь: Покупает
Атрибут связи: розничная цена
Сущность2: ПРОДУКТ
Сущность3: ПОСТАВЩИК
КЛИЕНТЫ покупают ПРОДУКТЫ у ПОСТАВЩИКОВ. Очевидно, что розничная цена потребует обращения ко всем трем сущностям для своей идентификации.
При двоичной связи, мы должны указывать две связи. Можно предположить, что при троичной связи необходимо устанавливать три. Поскольку атрибут связи уже установлен, давайте рассмотрим на другие возможные варианты:
Сущность1: КЛИЕНТ
Сущность2: ПОСТАВЩИК
Сущность3: ПРОДУКТ
КЛИЕНТЫ покупают у ПОСТАВЩИКОВ ПРОДУКТЫ
Для того же значения Сущности1 смысл утверждения остается прежним, и не добавляет никакой информации к процессу. Предположим что:
Сущность1: ПРОДУКТ
Сущность2: КЛИЕНТ
Сущность3: ПОСТАВЩИК
ПРОДУКТЫ покупаются КЛИЕНТАМИ у ПОСТАВЩИКОВ
В упрощенной версии описания диаграммы, мы получаем небольшую долю информации вследствие повторений. Предполагается, что нужно пробовать другие комбинации. Но, в упрощенном описании предполагается что одного утверждения, выведенного из семантики ситуации, должно быть достаточно для установления природы связи.
Более точная грамматика
Более точная грамматика для n-ой связи будет получена путем расширения грамматики для двоичных связей. В отличие от упрощенного случая, в более детальном грамматическом представлении будет необходимо делать три утверждения, по одному для каждой сущности. В случае двоичной связи M:N с полным участием, мы использовали следующее описание связи:
Шаблон 3 - M:N, полное участие со стороны М
В краткой форме:x должен быть связан со множеством y, что фактически означает:
В полной форме: x, записанный в базе данных, должен быть связан со множеством (одним или более) y. Не существует х, связанных с не-y, или не существует х, не связанных с y. (Отрицание будет зависеть от смысла утверждения).
Мы могли обобщить шаблоны структурных ограничений следующим образом:
Шаблон 4 - k:M, полное участие со стороны k (k = 1 или M)
В краткой форме: так же, как и выше
В полной форме: также как, и выше
Для n-ой связи мы расширим данное обобщенное утверждение, применив логический оператор "и":
Шаблон 5 (n-ая связь) x:y:z::a:b:c, частичное участие со стороны а.
В краткой форме: x должен/может быть связан со множеством y и множеством z
"Должен" соответствует полному участию; "может" – частичному. Коэффициент связи "a" не будет иметь значения. "b" и "c" заставляют нас говорить "один" или "много" в данном утверждении. Так, например, полная форма записи для x будет следующей:
В полной форме: x, записанный в базу данных, должен быть связан:
b = m [со множеством (одним или более)] y
b = 1 [с одним и только одним] y
и (или другие связующие слова [из, к, …])
c = m [со множеством (одним или более)] z
c = 1 [с одним и только одним] z.
Ни один x не связан более, чем с одним z.
Ни один x не связан более, чем с одним y.
Пример.
Для связи КЛИЕНТЫ:ПРОДУКТЫ:ПРОДАВЦЫ::M1:M2:M3 с полным участием со всех сторон:
В краткой форме: КЛИЕНТЫ должны покупать много ПРОДУКТОВ у многих ПРОДАВЦОВ.
В полной форме: КЛИЕНТЫ, записанные в базе данных, должны покупать много (один или более) ПРОДУКТОВ у многих (одного или более) ПРОДАВЦОВ.
Другие грамматические выражения строятся аналогично:
Продукты, записанные в базе данных, должны покупаться многими (одним или более) клиентами у многих (одного или более) продавцов.
Продавцы, записанные в базе данных, должны продавать много (один или более) продуктов многим (одному или более) клиентам.
Возможно и отрицание: Никакой клиент (в этой базе данных) не покупает продукты у не-продавцов.
Как и в случае с двоичными связями, отрицательные утверждения могут дополнять описание, если они имеют смысл.
Троичная связь при ситуациях связь-связи
Другой ситуацией, при которой троичная связь становится необходимой, может быть такова – при разработке модели возникает связь связи. В Chen-модели ER диаграммы не допускают связей связи; поэтому для корректного отображения ситуации необходимо установить троичную связь.
Например, начнем с двух сущностей: ИЗДАТЕЛЬ_КНИГИ (BOOK_PUBLISHER) и РУКОПИСЬ (MANUSCRIPT). Мы можем первоначально связать две сущности, как показано на Рисунке 7.6A. ИЗДАТЕЛЬ_КНИГИ редактирует РУКОПИСЬ.
Рисунок 7.6A: Двоичная связь ИЗДАТЕЛЬ_КНИГИ и РУКОПИСЬ
Далее, если некоторая РУКОПИСЬ в результате редактирования становится КНИГОЙ, это называется связью связи, как показано на Рисунке 7.6B. Эта связь связи становится здесь необходимой, поскольку ИЗДАТЕЛЬ_КНИГИ, связь редактирует, и РУКОПИСЬ, взятые вместе будут в результате порождать КНИГУ, как показано на Рисунке 7.6C.
Рисунок 7.6B: Связь связи
На Рисунке 7.6C, ИЗДАТЕЛЬ_КНИГИ, связь редактирует и РУКОПИСЬ, взятые вместе – создают класс более высокого уровня, состоящий из сущности ИЗДАТЕЛЬ_КНИГИ, связи редактирует и сущности РУКОПИСЬ. Этот составной класс (двух сущностей и связи) затем должен быть связан с КНИГОЙ, как показано на Рисунке 7.6C.
Рисунок 7.6C: Связь связи
Для того, чтобы корректно отобразить такую ситуацию на ER-диаграмме Chen-модели, нам необходимо создать слабую сущность (то есть, РЕДАКЦИЯ) и связать с сущностями ИЗДАТЕЛЬ_КНИГИ, РУКОПИСЬ, и КНИГА, как изображено на Рисунке 7.6D. Пересекающий атрибут, BMR, должен идентифицироваться сущностями ИЗДАТЕЛЬ_КНИГИ, РУКОПИСЬ, и РЕДАКЦИЯ. Эта редакция в результате может порождать КНИГУ (как показано на Рисунке 7.6D).
Рисунок 7.6D: Связь связи преобразуется в троичную связь
N-ые связи, сводящиеся к двоичным связям
Наличие трех связанных сущностей еще не означает троичную связь между ними. В данном разделе мы покажем, как можно преобразовывать троичные связи в двоичные, а затем приведем другой пример, иллюстрирующий, что реальная троичная связь не может быть сведена к двоичной.
n-связи могут быть преобразованы примерно таким же образом, как двоичная связь M:N может быть разложена на две связи. Сначала рассмотрим разложение связи M:N на две связи 1:M. (Рисунок 7.7). Идея заключается в том, чтобы сделать связь сущностью, и затем установить простые двоичные связи.
Рисунок 7.7: ER Диаграмма связи M:N, которая заменена двумя связями 1:M
Теперь обратимся к Рисунку 7.5. Если мы разложим Рисунок 7.5 на три двоичных связи, мы получим Рисунок 7.8. Заметим, что на Рисунке 7.8 новая сущность ПОСЕЩАЕМОСТЬ является слабой и зависит от трех сущностей: ФАКУЛЬТЕТ, СТУДЕНТ, и ВЫПУСК.
Рисунок 7.8: ER Диаграмма (только с первичными ключами), показывающая разложение троичной связи
на три двоичных
Существуют ситуации, при которых связь, по сути, соединяет более, чем две сущности. Рассмотрим Рисунок 7.2 в качестве примера. Если бы у нас имелся еще один атрибут, такой как заказ, который клиент делает поставщику на некоторые продукты, то этому атрибуту были бы необходимы все три сущности, то есть КЛИЕНТ, ПРОДУКТ и ПОСТАВЩИК. Заказ будет определять, что поставщик должен поставлять некоторый объем продукции клиентам. Такая связь не может в достаточной мере быть выражена с помощью двоичной связи. При двоичной связи мы можем только сказать, что клиент заказал продукт, или поставщик получил заказ на продукт. Тот факт, что клиент заказывает продукт, не подразумевает, что клиент C получает продукт P от поставщика S, если все три сущности не связаны.
Контрольные вопросы 7.2
1. Все ли троичные связи быть выражены в форме двоичных связей? Объясните.
2. Придумайте некоторые атрибуты и сущности связи, которые могли бы стать троичной связью. Может ли эта связь быть выражена в форме двоичной связи?
Преобразование троичных диаграмм в реляционную базу данных
В данном разделе мы рассматриваем правила преобразования n-ых связей в реляционную базу данных.
M6 – Для n-ых связей. Для каждой n-ой связи, создается новое отношение (таблица). В это отношение включаются все атрибуты связи. Затем включаются все ключи связанных сущностей в качестве внешних ключей. Определяются все внешние ключи. Первичным ключом нового отношения становится совокупность внешних ключей.
Например, вернемся к Рисунку 7.2. Имеется троичная связь покупает объединяющая сущности ПРОДУКТ, ПОСТАВЩИК и КЛИЕНТ. Пересекающим атрибутом является цена. Полученное в результате преобразования отношение (с некоторыми данными) будет таким:
Контрольные вопросы 7.3.
1. Может ли Рисунок 7.3 описываться только с помощью двоичной связи? Обсудите.
2. Каким правила преобразования следует применить для диаграммы на Рисунке 7.3?
3. Преобразуйте Рисунок 7.3 в реляционную базу данных и приведите пример данных.
Методология ER проектирования теперь представляется следующим образом:
Методология ER проектирования
Шаг 1: Выбрать из описания требований к базе данных одну первичную сущность и указать атрибуты, которые будут принадлежать данной сущности. При возможности выделить ключ и привести пример данных.
Шаг 2: Для описания базы данных использовать структурный английский язык для сущностей, атрибутов и ключей.
Шаг 3: Исследовать атрибуты в первичной сущности (возможно с помощью пользователя), чтобы выявить нужно ли записывать информацию о каких-либо атрибутах.
Шаг 3a: Если необходима информация об атрибуте, сделать атрибут сущностью и затем
Шаг 3b: Определите ее связь с родительской сущностью.
Шаг 3с: Если новая сущность для своего существования должна полностью зависеть от другой сущности, обозначить ее как слабую (в двойном прямоугольнике) и показать связь с идентифицирующей сущностью в двойном ромбе. Участие слабой сущности в связи является полным. Подчеркнуть пунктиром частичный ключ, идентифицирующий слабую сущность.
Шаг 4: Если можно выделить еще одну сущность, изобразить диаграмму для этой сущности и ее атрибутов. Повторить шаг 2 чтобы выяснить, возможно ли дальнейшее выделение сущностей.
Шаг 4a: Если дополнительная сущность или сущности не имеют потенциальных ключей, то изобразить их как слабые сущности (как описано на шаге 3c) и указать связь с идентифицирующей сущностью. Участие слабой сущности в связи является полным, или обязательным. Подчеркнуть пунктиром частичный ключ, идентифицирующий слабую сущность.
Шаг 5: Определить связи между сущностями (одну или несколько), если таковые существуют.
Шаг 6: Определить на структурированном английском языке точный характер связей с обеих сторон. Например, связь A:B::1:M означает связь A с B вида один-ко-многим с одной стороны и связь B с A вида многие-к-одному с другой стороны.
Шаг 6a: Изучить список атрибутов и определить, есть ли среди них такие, которые идентифицируются двумя (или более) сущностями. Если таковые имеются, прикрепить их к соответствующей связи, соединяющей сущности.
Шаг 6b. Изучить диаграмму на наличие петель, указывающих на избыточные связи. Если связь действительно является избыточной, ее следует удалить.
Шаг 7: Привести пример данных.
Шаг 8: Представить «разработанную» базу данных пользователю, дополнив ее английским описанием всех сущностей, ключей, атрибутов и связей. Пересмотреть диаграмму в случае необходимости.
Итоги Главы
Двоичные связи – наиболее часто встречающийся тип связей, и некоторые моделиERдиаграмм не имеют выражений для описания троичных или связей более высокого порядка; то есть все выражается в терминах двоичной связи. В этой главе мы показали, каким образом возникает необходимость троичной связи в отдельных случаях; например, когда есть перекрывающий атрибут, которому необходимы все три сущности для идентификации, или когда возникает связь связи. Троичные связи могут также быть разработаны методом обратного проектирования, который обсуждается в Главе 9. Также в этой главе, мы подробно обсудили структурные ограничения на троичные связии их грамматику, а также показали, как некоторые троичные или n-ые связи могут быть сведены к двоичным и как некоторые не могут быть сведены к двоичным связям. В последней части этой главы приводились правила преобразования n-ых связей.
Упражнения Главы 7
Упражнение 7.1
В Главе 5 была описана база данных, которая имела две сущности: КУРС и ПРЕПОДАВАТЕЛЬ. "Учебник" была атрибутом сущности КУРС. Расширьте базу данных, включив учебник в качестве сущности. Атрибутами сущности УЧЕБНИК могут быть: название книги, автор, цена, издание и издатель. Изучитесвязи, которые могли здесь возникнуть. Изобразите ER-диаграмму по крайней мере с двумя связями, одна из них должна быть троичной. Какими должны быть некоторые атрибуты связи?
Упражнение 7.2
Создайте ER диаграмму для агента, акций, и покупателя. Включите в диаграмму цену акции, выплачиваемую комиссию, имя и адрес агента, имя и адрес покупателя, эмблему акции и ее цену. Включите в диаграмму долю акций покупателя (Вы можете выбрать будет ли это учитываться агентом, или нет).
Упражнение 7.3
Используя три сущности - ПРЕПОДАВАТЕЛЬ, ГРУППА, АУДИТОРИЯ – составьте ER-диаграмму, которая отображает следующее: У каждой ГРУППЫ в АУДИТОРИИ может быть только один ПРЕПОДАВАТЕЛЬ, а у каждого ПРЕПОДАВАТЕЛЯ в АУДИТОРИИ может быть много ГРУПП, и каждый ПРЕПОДАВАТЕЛЬ ГРУППЫ может быть во многих АУДИТОРИЯХ.
Список литературы
Elmasri, R. and Navathe, S.B., Fundamentals of Database Systems, 3rd
ed., Addison Wesley, Reading, MA, 2000.
Teorey, T.J., Database Modeling and Design, Morgan Kaufman, San Francisco, 1999.
Teorey, T.J., Yang, D., and Fry, J.P., "A Logical Design Methodology for Relational Databases Using the Extended Entity-Relationship Model,"
ACM Computing Surveys, 18(2), 197–222, June 1986.