5.4. Проверка значимости и подбор модели с использованием коэффициентов детерминации. Информационные критерии

Ранее мы неоднократно задавались вопросом о том, как следует интерпретировать значения коэффициента детерминации с точки зрения их близости к нулю или, напротив, их близости к единице.

Естественным было бы построение статистической процедуры проверки значимости линейной связи между переменными, основанной на значениях коэффициента детерминации 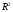– ведь является статистикой, поскольку значения этой случайной величины вычисляются по данным наблюдений. Теперь мы в состоянии построить такую статистическую процедуру.

Представим -статистику критерия проверки значимости регрессии в целом в виде

Отсюда находим:

Большим значениям статистики соответствуют и большие значения статистики , так что гипотеза, отвергаемая при=, должна отвергаться при выполнении неравенства, где

При этом вероятность ошибочного отклонения гипотезы 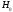по-прежнему равна.

Интересно вычислить критические значения при для различного количества наблюдений.

Ограничимся здесь простой линейной регрессией , так что

В зависимости от количества наблюдений , получаем следующие критические значения:

n	3	4	10	20	30	40	60	120	500
R2crit	0.910	0.720	0.383	0.200	0.130	0.097	0.065	0.032	0.008

Иначе говоря, при большом количестве наблюдений даже весьма малые отклонения наблюдаемого значения 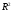от нуля оказываются достаточными для того, чтобы признать значимость регрессии, т. е. статистическую значимость коэффициента при содержательной объясняющей переменной.

Поскольку же значение равно приквадрату выборочного коэффициента корреляции между объясняемой и (нетривиальной) объясняющей переменными, то аналогичный вывод справедлив и в отношении величины этого коэффициента корреляции, только получаемые результаты еще более впечатляющи:

n	3	4	10	20	30	40	60	120	500
rxycrit	0.953	0.848	0.618	0.447	0.360	0.311	0.254	0.179	0.089

Если сравнивать модели по величине коэффициента детерминации R², то с этой точки зрения полная модель всегда лучше (точнее, не хуже) редуцированной – значение R² в полной модели всегда не меньше, чем в редуцированной, просто потому, что в полной модели остаточная сумма квадратов не может быть больше, чем в редуцированной.

Действительно, в полной модели с объясняющими переменными минимизируется сумма

по всем возможным значениям коэффициентов . Если мы рассмотрим редуцированную модель, например, без-ой объясняющей переменной, то в этом случае минимизируется сумма

по всем возможным значениям коэффициентов , что равносильно минимизации первой суммы по всем возможным значениямпри фиксированном значении. Но получаемый при этом минимум не может быть больше чем минимум, получаемый при минимизации первой суммы по всем возможным значениям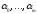, включая и все возможные значения. Последнее означает, чтов полной модели не может быть меньше, чем в редуцированной модели. Поскольку же полная сумма квадратов в обеих моделях одна и та же, отсюда и вытекает заявленное выше свойство коэффициента.

Чтобы сделать процедуру выбора модели с использованием более приемлемой, было предложено использовать вместо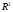егоскорректированный (adjusted) вариант

в который по-существу вводится штраф за увеличение количества объясняющих переменных. При этом,

так что

при и.

При использовании коэффициента 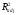для выбора между конкурирующими моделями, лучшей признается та, для которой этот коэффициент принимаетмаксимальное значение.

Замечание. Если при сравнении полной и редуцированных моделей оценивание каждой из альтернативных моделей производится с использованием одного и того же количества наблюдений, то тогда, как следует из формулы, определяющей 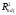, сравнение моделей по величинеравносильно сравнению этих моделей по величинеили по величине. Только в последних двух случаях выбирается модель сминиимальным значением (или).

Пример. Продолжая последний пример, находим значения коэффициента при подборе моделей,,:

для –

для –

для –

Таким образом, выбирая модель по максимуму , мы выберем из этих трех моделей именно модель, к которой мы уже пришли до этого, пользуясь- и-критериями.

В этом конкретном случае сравнение всех трех моделей по величине не равносильно сравнению их по величине(или), если модели,оцениваются по всемнаблюдениям, представленным в таблице данных, тогда как модельоценивается только понаблюдениям (одно наблюдение теряется из-за отсутствия в таблице запаздывающего значения, соответствующегогоду).

Наряду со скорректированным коэффициентом детерминации, для выбора между несколькими альтернативными моделями часто используют так называемые информационные критерии: критерий Акаике и критерий Шварца, также «штрафующие» за увеличение количества объясняющих переменных в модели, но несколько отличными способами.

Критерий Акаике (Akaike’s information criterion – AIC). При использовании этого критерия, линейной модели с объясняющими переменными, оцененной понаблюдениям, сопоставляется значение

где - остаточная сумма квадратов, полученная при оценивании коэффициентов модели методом наименьших квадратов. При увеличении количества объясняющих переменных первое слагаемое в правой части уменьшается, а второе увеличивается. Среди нескольких альтернативных моделей (полной и редуцированных) предпочтение отдается модели с наименьшим значением, в которой достигается определенный компромисс между величиной остаточной суммы квадратов и количеством объясняющих переменных.

Критерий Шварца (Schwarz’s information criterion – SC, SIC). При использовании этого критерия, линейной модели с объясняющими переменными, оцененной понаблюдениям, сопоставляется значение

И здесь при увеличении количества объясняющих переменных первое слагаемое в правой части уменьшается, а второе увеличивается. Среди нескольких альтернативных моделей (полной и редуцированных) предпочтение отдается модели с наименьшим значением .

Пример. В последнем примере получаем для полной модели и редуцированных моделейиследующие значенияи.

	AIC	SC
M3	8.8147	8.9594
M2	8.6343	8.7428
M1	8.4738	8.5462

Предпочтительной по обоим критериям оказывается опять модель .

Замечание. В рассмотренном примере все три критерия 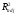,ивыбирают одну и ту же модель. В общем случае подобное совпадение результатов выбора вовсе не обязательно.

Включение в модель большого количества объясняющих переменных часто приводит к ситуации, которую называют мультиколлинеарностью.

Мы обещали ранее коснуться проблемы мультиколлинеарности и сейчас выполним это обещание. Прежде всего, напомним наше предположение (4) матрица X^TX невырождена, т. е. ее определитель отличен от нуля:

которое можно заменить условием

(4^’) столбцы матрицы X линейно независимы.

Полная мультиколлинеарность соответствует случаю, когда предположение (4) нарушается, т. е. когда столбцы матрицы линейно зависимы, например,

(-й столбец является линейной комбинацией остальных столбцов матрицы). При наличии чистой мультиколлинеарности система нормальных уравнений не имеет единственного решения, так что оценка наименьших квадратов для вектора параметров (коэффициентов) попросту не определена однозначным образом.

На практике, указывая на наличие мультиколлинеарности, имеют в виду осложнения со статистическими выводами в ситуациях, когда формально условие (4) выполняется, но при этом определитель матрицы X^TX близок к нулю. Указанием на то, что -я объясняющая переменная «почти является» линейной комбинацией остальных объясняющих переменных, служит большое значениекоэффициента возрастания дисперсии

оценки коэффициента при этой переменной вследствие наличия такой «почти линейной» зависимости между этой и остальными объясняющими переменными. Здесь - коэффициент детерминации при оценивании методом наименьших квадратов модели

Если , то, и это соответствует некоррелированности-ой переменной с остальными переменными. Если же, то тогда, и чем больше корреляция-ой переменной с остальными переменными, тем в большей мере возрастает дисперсия оценки коэффициента при-ой переменной по сравнению с минимально возможной величиной этой оценки.

Мы можем аналогично определить коэффициент возрастания дисперсии оценки коэффициента при-ой объясняющей переменной для каждого:

Здесь — коэффициент детерминации при оценивании методом наименьших квадратов модели линейной регрессии-ой объясняющей переменной на остальные объясняющие переменные. Слишком большие значения коэффициентов возрастания дисперсии указывают на то, что статистические выводы для соответствующих объясняющих переменных могут быть весьма неопределенными: доверительные интервалы для коэффициентов могут быть слишком широкими и включать в себя как положительные, так и отрицательные значения, что ведет, в конечном счете, к признанию коэффициентов при этих переменных статистически незначимыми при использовании- критериев.

Пример. Обращаясь опять к данным об импорте товаров и услуг во Францию, находим:

Коэффициенты возрастания дисперсии для переменных исовпадают вследствие совпадения коэффициентов детерминации регрессии переменнойна переменныеии регрессии переменнойна переменныеи(взаимно обратные регрессии).

Полученные значения коэффициентов возрастания дисперсий отражают очень сильную коррелированность переменных и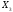. (Выборочный коэффициент корреляции между этими переменными равен.)

При наличии мультиколлинеарности может оказаться невозможным правильное разделение влияния отдельных объясняющих переменных. Удаление одной из переменных может привести к хорошо оцениваемой модели. Однако оставшиеся переменные примут на себя дополнительную нагрузку, так что коэффициент при каждой из этих переменных измеряет уже не собственно влияние этой переменной на объясняемую переменную, а учитывает также и часть влияния исключенных переменных, коррелированных с данной переменной.

Пример. Продолжая последний пример, рассмотрим редуцированные модели, получаемые исключением из числа объясняющих переменных переменной или переменной. Оценивание этих моделей приводит к следующим результатам:

c идля коэффициента при;

c идля коэффициента при.

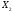В каждой из этих двух моделей коэффициенты при иимеют очень высокую статистическую значимость. В первой модели изменчивость переменнойобъясняетизменчивости переменной; во второй модели изменчивость переменнойобъясняет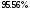изменчивости переменной. 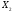С этой точки зрения, переменныеивполне заменяют друг друга, так что дополнение каждой из редуцированных моделей недостающей объясняющей переменной практически ничего не добавляя к объяснению изменчивости(в полной модели объясняетсяизменчивости переменной), в то же время приводит к неопределенности в оценивании коэффициентов прии.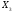

Но коэффициент при в полной модели соответствует связи между переменнымии, очищенными от влияния переменной, тогда как коэффициент прив полной модели соответствует связи между переменнымии, очищенными от влияния переменной. Поэтому неопределенность в оценивании коэффициентов приив полной модели по-существу означает невозможность разделения эффектов влияния переменныхина переменную.

Приведем значения 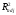,идля всех трех моделей.

Полная	0.9702	1.1324	3.274	3.411
Без	0.9704	1.1286	3.211	3.303
Без	0.9719	1.0991	3.158	3.250

Все четыре критерия выбирают в качестве наилучшей модель с исключенной переменной .

Мы не будем далее углубляться в проблему мультиколлинеарности, обсуждать другие ее последствия и возможные способы преодоления затруднений, связанных с мультиколлинеарностью. Заинтересованный читатель может обратиться по этому вопросу к более полным руководствам по эконометрике.

5. Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками.

Итак, при исследовании остатков _i должно проверяться наличие следующих пяти предпосылок МНК:

1. случайный характер остатков;

2. нулевая средняя величина остатков, не зависящая от х_i;

3. гомоскедастичность – дисперсия каждого отклонения _i одинакова для всех значений х_i;

4. отсутствие автокорреляции остатков – значения остатков _i распределены независимо друг от друга;

5. остатки подчиняются нормальному распределению.

Если распределение случайных остатков _i не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

В случае нарушения первых двух предпосылок необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии.

Пятая предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F. Однако и при нарушении пятой предпосылки МНК оценки регрессии обладают достаточной состоятельностью.

Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок.

Если не соблюдается гомоскедастичность, то имеет место гетероскедастичность. Наличие гетероскедастичности может привести к смещенности оценок коэффициентов регрессии, а также к уменьшению их эффективности. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющихся. В этом случае рекомендуется применять обобщенный метод наименьших квадратов, который заключается в том, что при минимизации суммы квадратов отклонений (5) отдельные ее слагаемые взвешиваются: наблюдениям с большей дисперсией придается пропорционально меньший вес. Чтобы убедиться в гетероскедастичности остатков и, следовательно, в необходимости использования обобщенного МНК, обычно не ограничиваются визуальной проверкой гетероскедастичности, а проводят ее эмпирическое подтверждение, в частности, используют метод Гольдфельда – Квандта. Проиллюстрируем его на примере (табл.5.3).

Поступления налогов в бюджет (y_i – млн.руб.) в зависимости

от численности работающих (х_i – тыс.чел). Таблица 5.3

№ п/п	хi	yi	ŷх	i
1	2	3	4	5
1	3	4,4	-1,0	5,4
2	6	8,1	2,5	5,6
3	8	12,9	4,9	8,0
4	18	20,8	16,6	4,2
5	20	15,5	19,0	-3,5
6	23	28,8	22,5	6,3
7	39	37,5	41,4	-3,9
8	49	48,7	53,2	-4,5
9	60	68,6	66,1	2,5
10	74	104,6	82,6	22,0
11	79	90,5	88,5	2,0
12	95	88,3	107,4	-19,1
13	106	132,4	120,4	12,0
14	112	122,0	127,4	-5,4
15	115	99,1	131,0	-31,9
16	125	114,2	142,7	-28,5
17	132	150,6	151,0	-0,4
18	149	156,1	171,0	-14,9
19	157	209,5	180,5	29,0
20	282	342,9	327,8	15,1
итого	1652	1855,5	1855,5	0,0

По выборочным данным строим уравнение регрессии

ŷ_х = – 4,565 + 1,178х.

Теоретические значения ŷ_х и отклонения от них фактических значений _i приведены в четвертой и пятой колонке табл.5.3. Очевидно, что остаточные величины _i обнаруживают тенденцию к росту по мере увеличения х и у. Этот вывод подтверждается и по критерию Гольдфельда – Квандта. Для его применения необходимо выполнить следующие шаги:

• упорядочить n наблюдений по мере возрастания переменной х (выполнено);

• исключить из рассмотрения k центральных наблюдений (рекомендовано при n=60 принимать k=16, при n=30 принимать k=8, при n=20 принимать k=4), в данном случае исключаем строки 9–12;

• разделить совокупность на две группы (по ń=(n – k):2=8 наблюдений соответственно с малыми и большими значениями фактора х) и определить по каждой из групп уравнения регрессии (результаты в табл.5.4.);

• определить остаточные суммы квадратов для первой (S₁) и второй (S₂) групп и найти их отношение R=S₂:S₁. Чем больше величина R превышает табличное значение F–критерия с ń –2 степенями свободы (приложение 2), тем более нарушена предпосылка о равенстве дисперсий остаточных величин, т.е. наблюдается гетероскедастичность остатков.

Таблица 5.4.

№ п/п	хi	yi	ŷх	i	i2
1	3	4,4	5,7	–1,3	1,69
2	6	8,1	8,5	–0,4	0,16
3	8	12,9	10,3	2,6	6,76
4	18	20,8	19,6	1,2	1,44
5	20	15,5	21,4	–5,9	34,81
6	23	28,8	24,2	4,6	21,16
7	39	37,5	38,9	–1,4	1,96
8	49	48,7	48,1	0,6	0,36
Уравнение регрессии: ŷх = 2,978 + 0,921х. Сумма S1=68,34
13	106	132,4	110,7	21,7	470,89
14	112	122,0	118,7	3,3	10,89
15	115	99,1	122,7	–23,6	556,96
16	125	114,2	136,1	–21,9	479,61
17	132	150,6	145,4	5,2	27,04
18	149	156,1	168,2	–12,1	146,41
19	157	209,5	178,9	30,6	936,36
20	282	342,9	346,1	–3,2	10,24
Уравнение регрессии: ŷх = 31,142 + 1,338х. Сумма S2 =2638,4

Величина R=2638,4 : 68,34=38.6 существенно превышает табличное значение F-критерия 4,28 при 5%-ном и 8,47 при 1%-ном уровне значимости для числа степеней свободы 8 – 2 = 6, подтверждая тем самым наличие гетероскедастичности.

Нарушение четвертой предпосылки МНК – автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных.

Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может обусловить автокорреляцию.

Инерция. Многие экономические показатели (например, инфляция, безработица, ВНП и т.п.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Действительно, экономический подъем приводит к росту занятости, сокращению инфляции, увеличению ВНП и т.д. Этот рост продолжается до тех пор, пока изменение конъюнктуры рынка и ряда экономических характеристик не приведет к замедлению роста, затем остановке и движению вспять рассматриваемых показателей. В любом случае эта трансформация происходит не мгновенно, а обладает определенной инертностью.

Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом). Например, предложение сельскохозяйственной продукции реагирует на изменение цены с запаздыванием (равным периоду созревания урожая). Большая цена сельскохозяйственной продукции в прошедшем году вызовет (скорее всего) ее перепроизводство в текущем году, а следовательно, цена на нее снизится и т.д.

Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его подинтервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может послужить причиной автокорреляции.

Последствия автокорреляции во многом сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяются следующие.

1. Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок.

2. Дисперсии оценок являются смешенными. Часто дисперсии, вычисленные по стандартным формулам, являются заниженными, что влечет за собой увеличение t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут не являться.

3. Оценка дисперсии регрессии является смещенной оценкой истинного значения дисперсии, во многих случаях занижая его.

В силу вышесказанного выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

Для обнаружения автокорреляции необходимо наблюдения упорядочить по значению фактора х (как в предыдущем примере) и составить ряды с текущими и предыдущими остатками. Коэффициент корреляции r_ij между _i и _j, где _i – остатки текущих наблюдений, _j – остатки предыдущих наблюдений (например, j=i–1) определяется по обычной формуле линейного коэффициента корреляции (2.1).Рассмотрим расчет коэффициента корреляции между _i и _j, взяв в качестве примера данные из табл.5.3 и перенеся их в табл. 5.5 (n=19).

Таблица 5.5.

№ п/п	i	i-1	ii-1
1	5,6	5,4	30.24
2	8,0	5,6	44.8
3	4,2	8,0	33.6
4	–3,5	4,2	–14.7
5	6,3	–3,5	–22.05
6	–3,9	6,3	–24.57
7	–4,5	–3,9	17.55
8	2,5	–4,5	–11.25
9	22,0	2,5	55
10	2,0	22,0	44
11	–19,1	2,0	–38.2
12	12,0	–19,1	–229.2
13	–5,4	12,0	–64.8
14	–31,9	–5,4	172.26
15	–28,5	–31,9	909.15
16	–0,4	–28,5	11.4
17	–14,9	–0,4	5.96
18	29,0	–14,9	–432.1
19	15,1	29,0	435
итого	–5.3998	–15.1031	922.09
среднее	–0,2842	–0,7949	48.5311

σ_i =15.1347, σ_j =14,7663 и в соответствие с (2.1)

r_ij =(48,5311 – (–0,2842)(–0,7949))/15,1347/14,7663=0,2161,

что при 17 степенях свободы явно незначимо и демонстрирует отсутствие автокорреляции остатков.

Автокорреляция остатков может быть вызвана несколькими причинами, имеющими различную природу. Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака. Во-вторых, причину следует искать в формулировке модели, которая может не включать существенный фактор, влияние которого отражается в остатках, вследствие чего они оказываются автокоррелированными. Очень часто этим фактором является фактор времени, поэтому проблема автокорреляции остатков весьма актуальна при исследовании динамических рядов, что мы рассмотрим в соответствующем разделе.