3. Поколения измерительных информационных систем

В развитии измерительных информационных систем можно отметить ряд поколений.

Первое поколение — формирование концепции ИИС: системная организация совместной автоматической работы средств получения, обработки передачи количественной информации. Системы первого поколения — это системы в основном централизованного циклического получения измерительной информации с элементами вычислительной техники на базе дискретной полупроводниковой техники. Этот этап (конец 1950-х — начало 1960-х гг.) принято назвать периодом детерминизма, так как для анализа в ИИС использовался хорошо разработанный аппарат аналитической математики.

Второе поколение (1970-е гг.) — использование адресного сбора информации, обработка информации с помощью встроенных ЭВМ. Элементную базу представляют микроэлектронные схемы малой и средней степени интеграции. Этот период характерен ре­шением целого ряда вопросов теории систем в рамках теории слу­чайных процессов и математической статистики, поэтому его принято называть периодом стохастичности.

Третье поколение характеризуется широким введением в ИИС БИС, микропроцессоров и микропроцессорных наборов, микро-ЭВМ и промышленных функциональных блоков, совместимых между собой по информационным, метрологическим, энергетическим и конструктивным характеристикам; созданием распреде­ленных ИИС. Этот период характерен тем, что появилось адаптивные ИИС.

Четвертое поколение — появление гибких перестраиваемых программируемых ИИС в связи с развитием системотехники и вычислительной техники.

В элементной базе резко возрастает доля интегральных схем большой и сверхбольшой степени интеграции.

Пятое поколение набирает силу и входит в жизнь народного хозяйства — это интеллектуальные и виртуальные измерительные информационные системы, построенные на базе ПЭВМ и совре­менного математического и программного обеспечения.

4. Математические модели и алгоритмы измерения измерительных информационных систем

Поскольку области применения ИИС весьма обширны (про­мышленное и сельскохозяйственное производство, медицина и космос, искусство и научный эксперимент, АСУТП и АСУ, связь и вычислительные системы), математические модели объектов столь же разнообразны. Однако методы математического модели­рования позволяют одинаковыми формулами представлять различные по своей природе объекты и использовать для исследова­ния и решения задач оптимизации и синтеза ИИС электронно-вычислительные машины и ПЭВМ.

Математическая модель объекта измерения включает в себя описание взаимодействия между переменными входа и выхода для установившегося и переходного состояний, т. е. модели статики и динамики: граничные условия и допустимое изменение переменных процесса.

Если переменные объекта изменяются только во времени, то модели, описывающие свойства таких объектов, называются моделями с сосредоточенными параметрами.

Модели объектов исследований, переменные которых изменяются как во времени, так и в пространстве, называются моделями с распределенными параметрами.

Форма записи математической модели может быть различна: алгебраические и трансцендентные уравнения, дифференциальные уравнения и уравнения в частных производных. Могут использоваться переходные и передаточные функций, частотные и спектральные характеристики и др.

Различают три основных метода получения математических моделей объектов исследования:

• аналитический;

• экспериментальный;

• экспериментально-аналитический.

В последние годы при создании ИИС широко используется математическое моделирование, реализующее цепочку: объект-модлель—вычислительный алгоритм—программа для ПЭВМ—рас­чет на ПЭВМ —анализ результатов расчета—управление объектом исследования.

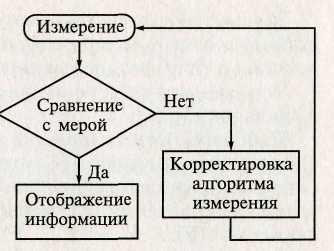
Рис. 3. К-сеть процедуры изме- Рис. 4. Блок-схема алгоритма измерения величины

Ядро вычислительного эксперимента модель—алгоритм—программа калибрует и формирует оптимальную модель объекта исследования.

Алгоритм измерения может быть представлен словесно, аналитически, графически или сочетанием этих методов.

Последовательность действий не произвольна, а реализует тот или иной метод решения задачи. Во всех случаях она должна быть настолько точно сформулирована, чтобы не осталось места для различных толкований и двусмысленностей.

Так, Э. И. Цветков оценку измеряемой величины представляет выражением

где Р_и — оператор, представляющий алгоритм измерений; X — сигнал, несущий информацию о значении измеряемой величины; Х_о — мера, образцовая величина, лежащая в основе операции сравнения.

Графически этот же процесс представлен на рис..3.

Тот же процесс М. П. Цапенко предлагает записать в форме содержательных логических схем алгоритмов (СЛСА), которая отражает параллельную работу самостоятельных измерительных каналов:

Наиболее простой и распространенной формой алгоритмической структуры является блок-схема, представленная на рис..4.

Измерительные системы могут быть ближнего или дальнего действия. На вход системы поступает множество изменяющихся во времени и (или) распределенных в пространстве величин {х,((, s)}f.

Упрощенная классификация измерительных систем представлена на рис. 5.

Наиболее распространены системы для прямых измерений. Обобщенная структура ИС подставлена на рис. 6. Для всех ИС основными элементами являются первичные преобразователи {Д}, элементы сравнения {С}, меры {М} и элементы отображения информации {В}.

Для совместных и совокупных измерений часто используют многомерные и аппроксимирующие системы.

Характеристики измерительных систем. Важнейшими характеристиками ИС являются эффективность, полнота выполняемых функций, достоверность, надежность, быстродействие, характеристики входов и выходов, метрология.

Рис. 5.

Эффективность. Под эффективностью понимается улучшение работы объекта при использовании системы. Ограничимся рассмотрением экономической эффективности систем, представляющих наибольший интерес для экономики. Приращение экономической эффективности можно выразить формулой

Рис.6. Обобщенная структура измерительной системы

где Э₂ — экономический эффект от объекта в тот же заданный промежуток времени с применением измерительной системы; Э[ — экономический эффект от объекта в заданный промежуток времени без измерительной системы.

Экономический эффект целесообразно рассчитывать по общепризнанному критерию полных затрат.

Для сравнения различных измерительных систем удобнее использовать нормированный показатель эффективности, называемый коэффициентом эффективности:

где Э„ — экономический эффект от объекта при использовании идеальной измерительной системы, выполняющей все свои функции при отсутствии на это затрат.

Коэффициент эффективности изменяется в пределах 0<г|<1. Определение и уточнение эффективности системы производится на нескольких этапах проектирования и эксплуатации системы. На всех этапах проектирования производится предварительная оценка по ожидаемым данным, которая уточняется после ввода ИИС в эксплуатацию.

Полнота (глубина) выполняемых функций. Она показывает, какая часть контролируемого или управляемого объекта охвачена измерительной системой.

Коэффициент, характеризующий полноту:

где N_k — число параметров объекта, охваченных измерительной системой; N — общее число параметров объекта (например, контроля, измерения, управления).

Во многих случаях целесообразно использовать информационный критерий полноты:

где I₀ — общее количество информации о состоянии объекта во всех параметрах контроля, измерения и управления; I_с — количество информации о состоянии объекта в параметрах, охваченных системой.

При этом все параметры объекта принимаются равнозначными, что существенно упрощает задачу за счет несовершенства отображающей ее модели. Тем не менее для ориентировочной предварительной оценки такой подход, допустим, отражает степень доверия к информации в системе.

Достоверность. Достоверность относится к обобщенным характеристикам. Требования, предъявляемые к этому показателю, являются исходными для обоснования частных характеристик системы. К наиболее существенным факторам достоверности относятся точность измерения контролируемых параметров, глубина контроля, надежность и помехоустойчивость работы всех устройств. С уменьшением достоверности возрастает вероятность неработоспособного состояния объекта контроля, измерения, управления при информации в системе в пределах допусков.

Характерным примером низкой достоверности является работа с низкой помехоустойчивостью в условиях помех. Аналогичная ситуация возникает при неудовлетворительной надежности системы или при недопустимо малой точности измерений. Универсальный критерий для определения достоверности различных измерительных систем еще не разработан, поэтому ограничимся методикой определения достоверности в отдельно рассматриваемой системе.

Надежность. Критерий надежности и его числовые характеристики выбираются с учетом особенностей назначения информационной системы и характера решаемых задач. К основным критериям надежности систем относятся:

• средняя наработка на отказ t;

• среднее время восстановления t_в;

• средняя наработка до отказа t₀;

• интенсивность отказов ;

• вероятность безотказной работы системы P(t) в течение заданного времени;

• вероятность завершения проверки объекта или группы объектов(вероятность восстановления) F(t_B) в течение заданного времени;

• коэффициент готовности системы К_г.

Для стационарных измерительных систем в экономике широко

используются критерии t_о, t_в и частично К_г.

В целях уменьшения влияния ненадежности на работоспособность системы используются два основных метода самоконтроля в измерительной системе: программный и схемный (аппаратурный).

Программный метод основан на использовании заранее отработанных испытательных программ (тестов). Такой самоконтроль в основном позволяет проверить устройства системы, производящие обработку информации.

Схемный самоконтроль требует дополнительного оборудования (аппаратуры) для проверки системы. Одной из разновидностей схемного самоконтроля является применение кодов с обнаружением и исправлением ошибок. Методы самоконтроля требуют временной, информационной или аппаратурной избыточности.

Быстродействие. Быстродействие характеризуется средним временем выполнения операций (измерения, контроля, управления, диагностики, поиска и т.п.). Для циклических систем быстродействие характеризуется временем цикла t_n. Во многих случаях при определении быстродействия необходимо учитывать среднее время выполнения вспомогательных операций t_всп, к которым относятся включение источников питания разогрева аппаратуры, подключение кабелей и т. п. В таких случаях быстродействие, например системы измерения, определяется выражением

t_ц = t_всп + t_осн +t_0н

где t_осн — среднее время самого контроля и поиска неисправностей; t_0н — среднее время считывания или записи и анализа результатов.

Быстродействие в ряде случаев удобно характеризовать, информационным критерием — количеством информации, перерабатываемой в единицу времени.

Для систем контроля и измерения быстродействие

где H_Oi —энтропия i-го параметра до начала контроля;H_i — энтропия i-го параметра после контроля; t_ko — время измерения определяющих параметров t_пн.„ — время поиска неисправностей.

В расчетах используется критерий Шеннона, учитывающий количество информации и возможности ее статистического кодирования.

Однако при расчете быстродействия во многих случаях целесо­образно использовать критерий Хартли, учитывающий только физические возможности системы. Тогда быстродействие эквивалентной информационной емкости определяется по формуле

где т — число различных состояний, например число уровней квантования в дискретной системе.

Характеристики входов и выходов системы. Они включают в себя перечень и данные входов системы, а также характеристики устройств отображения информации. К последним относятся данные диспетчерского щита и пульта, данные дисплеев и других средств отображения информации.

Характеристики технических средств. Эти характеристики включают в себя данные элементной базы (типы и серии микросхем и других элементов), типы готовых блоков, устройств и вспомогательного оборудования, включая в себя источники питания. Дается характеристика условий эксплуатации системы.

Многоканальные (параллельного действия) ИС. Это один из наиболее распространенных видов ИИС, обладающих наиболее высокой надежностью более высоким быстродействием при одновременном получении информации, возможностью подбора средств измерений к замеряемым величинам, что может исключить унификацию сигналов. Однако они имеют повышенные сложность и стоимость (рис..7.)

Мультиплицированные (с общей образцовой величиной) ИС. Эти системы предложены Ф. Е. Темниковым (рис..8). Их еще называют системами с развертывающим уравновешиванием. Системы имеют меньшее число элементов, чем многоканальные ИС, но несколько меньшее быстродействие.

В этих системах измерительная величина сравнивается с линейно изменяющейся величиной. При фиксированных моментах начала развертки и равенства х и х_к может быть определен интер-

Системы

Рис. 26.7. Структурная схема много- Рис. 26.8. Структурная схема канальной ИС мультиплицированной ИС

вал времени t_x, пропорциональный значению х_к. В многоканальной системе возникают трудности в разделении сигналов от элементов сравнения. В этом случае прибегают к специальным мерам

СканирующиеИС

Эти системы с помощью одного канала выполняют последовательно измерения множества величин и имеют сканирующее устройство (СкУ), которое перемещает датчик в пространстве

Траектория движения при пассивном сканировании может быть запрограммирована, при активном сканировании может изменятся в зависимости от получаемой измерительной информации.

Сканирующие системы применяют для измерения температурных полей, нахождения экстремальных значений исследуемых полей (давлений, механических напряжений и т.д.) или нахождения одинаковых значений параметра. Недостаток систем — малое быстродействие.

Многоточечные (последовательно-параллельного действия) ИС. Их применяют в сложных объектах с большим числом измеряемых параметров (рис. 9).

В этих системах при множестве датчиков {Д,}" имеется всего один измерительный канал (рис. 9, а) и измерительный коммутатор SW либо множество датчиков {Д,}" и множество индикаторов {В,} (рис. 9, б).

Рис. 9

Измерительные коммутаторы служат для согласования параллельных и последовательных элементов во времени. Они должны обладать определенными метрологическими характеристиками (погрешность, быстродействие и др.)- Лучшие по точности результаты дают контактные измерительные коммутаторы (относительная погрешность составляет 10~⁵... 10~⁶), но они имеют низкое быстродействие, малое количество коммутируемых цепей и не работают по заявкам. Бесконтактные измерительные коммутаторы име­ют более низкую точность (относительная погрешность составляет 10~³... КИ), но значительно лучшие остальные показатели.

Недостаток систем — пониженные быстродействие и точность за счет использования ключей коммутаторов.

Многомерные ИС. Эти системы основаны на одновременном измерении различных свойств среды, зависящих от ее состава, с последующей математической обработкой результатов измерения.

Измеряемыми могут быть, например, электропроводность и плотность, температура кипения и показатель преломления или удельный вес и т.д. Во всех случаях независимо от характера выполняемого расчета возможность измерения связана с возможностью составления системы независимых уравнений:

где■ Х1 ..., Хь ••-, X_k-1 — измеряемые параметры анализируемой среды; С_ь С₂, С₃, ..., Q_i} ..., С_к — концентрации компонентов анализируемой среды;/_ь ...,f_b ...,f_k-1— функции, выражающие характер зависимости измеряемых параметров от состава среды.

Выполнение функциональной независимости уравнений системы обеспечивает принципиальную возможность ее решения, т. е. нахождения нужного С_к. Данные системы обеспечивают таким образом избирательное определение величин интересующего нас компонента в многокомпонентной среде путем применения недостаточно избирательных измерительных средств.

Аппроксимирующие измерительные системы (АИС). Их применяют при необходимости количественно оценить или восстановить исходную величину, являющуюся функцией некоторого аргумента. Есть два пути выполнения этих измерений: первый — измерение дискретной величины и восстановление ее путем аппроксимации с помощью многочленов; второй — измерение коэффициентов многочленов, аппроксимирующих исходную функцию на всем интервале ее исследования.

Основные области применения АИС — это измерение статистических характеристик случайных процессов, характеристик нелинейных элементов, сжатие, фильтрация, генерация сигналов заданной формы.