
ZO-2012 Физика задания для контрольной
.pdfW электростатического поля внутри цилиндра, приходящуюся на 1 м этого цилиндра. Цилиндр находится в вакууме.
233. Шар радиуса R1 = 10 см заряжен до потенциала ϕ1 = 300 В, а шар радиуса R2 = 15 см – до потенциала ϕ2 = 600 В. Шары привели в соприкосновение друг с другом. Какая по величине энергия W выделится при этом? Принять, что шары находятся в жидкости с диэлектрической проницаемостью ε = 6,5.
234. В вакууме радиус равномерно заряженной сферической оболочки увеличивается от R1 = 5 см, до R2 = 10 см. Найти работу A12 сил поля, если заряд оболочки Q = 1,15 мкКл.
235.Две концентрические сферы несут равномерно распределенные заряды Q1 = −2Q2 = 5 мкКл. Радиус первой сферы R1 = 0,5 м, радиус второй сферы R2 =
=4 м. Пространство между сферами заполнено изотропным диэлектриком с ε =
=6,5. Найти энергию электростатического поля W между этими сферами.
236.Заряд равномерно распределен по объему изотропного диэлектрика (ε =
=3), имеющего форму шара. Радиус шара R = 20 см, объёмная плотность заряда
ρ= 15 нКл/м3. Определить энергию W электростатического поля внутри шара.
Шар находится в вакууме.
237. Электрическое поле создано в вакууме двумя бесконечными параллельными пластинами, несущими равномерно распределенные заряды с поверхностными плотностями σ1 = 5 нКл/м2 и σ 2 = –15 нКл/м2, которые расположены на расстоянии d = 10 см друг от друга. Между пластинами находится слой изотропного диэлектрика с ε = 7. Определить: а) объемную плотность энергии электростатического поля ω между пластинами и вне пластин; б) энергию W электростатического поля между пластинами, приходящуюся на 1 м2 поверхности пластины.
238. Бесконечно длинный эбонитовый (ε = 3) цилиндр радиусом R = 5 см равномерно заряжен с объемной плотностью ρ . Чему равен радиус R1 коаксиального (соосного) цилиндра, разделяющего заряженный цилиндр на две соосные части, энергии W которых равны?
239. Точечный заряд Q = 1,5 мкКл находится в центре шарового слоя из изотропного диэлектрика (ε = 2). Внутренний радиус слоя R1 = 2 м, внешний – R2 = = 3 м. Найти энергию электростатического поля W в пространстве, ограниченном концентрическими сферами радиусом R3 = 0,5 м и R4 = 5 м. Принять, что вне диэлектрика величина ε = 1.
240. Два бесконечно длинных коаксиальных цилиндра равномерно заряжены с линейными плотностями τ1 = – 0,5 и τ 2 = 750 нКл/м. Радиус первого цилиндра R1 = 1 см, радиус второго – R2 = 4 см. Пространство между цилиндрами заполнено изотропным диэлектриком с ε = 3. Найти энергию электростатического поля W между цилиндрами, приходящуюся на 1 м их длины.
50

Тема 14. Электрический ток. Закон Ома для однородного и неоднородного участков электрической цепи. Работа и мощность постоянного тока.
Закон Джоуля – Ленца
Пример решения задач
1. Сила тока в проводнике равномерно нарастает от I0 = 0 до I = 3,00 А в течении времени τ = 10,0 с. Определить зарядQ , прошедший в проводнике.
|
Дано |
|
Анализ и решение |
|
||||||
I = I0 + kt |
|
Так как сила тока в проводнике изменяется со временем, то |
||||||||
|
||||||||||
I0 |
= 0 |
|
воспользоваться для подсчета заряда формулой |
Q = It нельзя. |
||||||
|
Поэтому возьмем дифференциал заряда dQ = Idt |
и проинтегри- |
||||||||
I |
= 3,00 А |
|
||||||||
τ |
= 10,0 с |
|
руем: |
|
|
|
|
τ |
|
|
Q = ? |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Q = ∫ Idt . |
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
Подставим в эту формулу выражение для тока, как функцию времени |
||||||||||
|
|
|
τ |
|
|
|
|
τ |
τ |
|
|
|
|
Q = ∫(I0 + kt)dt =I0 ∫ dt + k ∫tdt . |
|
||||||
|
|
|
0 |
|
|
|
|
0 |
0 |
|
Полученное выражение проинтегрируем по времени |
|
|||||||||
|
|
|
|
|
t |
2 |
|
τ |
τ 2 |
|
|
|
|
|
|
|
|
||||
|
|
|
Q = (I |
t + k |
|
= (I τ + k |
|
|||
|
|
|
|
|
) |
) . |
(1) |
|||
|
|
|
|
|
||||||
|
|
|
0 |
2 |
|
0 |
2 |
|
||
|
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
Значение коэффициента пропорциональности k найдем из формулы I = I0 + kt , если заметим, что при t = 10,0 c, I = 3,00 A
k= (I − I0 ) = 3,00 = 0,30 A/c.
τ10,0
Проверим наименование единицы измерения заряда в системе СИ
|
A × c2 |
|
н.е.и. Q = A × c + |
|
= Кл. |
|
||
|
c |
|
Подставив значения физических величин в формулу (1), найдем
Q = 0 ×τ + 0,30 (10,0)2 =15,0 Кл. 2
Ответ: заряд, прошедший по проводнику Q = 15,0 Кл.
2. Сила тока в проводнике сопротивлением R = 12,0 Ом равномерно убывает в течение времени t = 2,00 с от I0 = 5,00 А, до I = 0. Какое количество теплоты Q1 , выделяется в этом проводнике за первую секунду, и Q2 – за вторую?
51
Дано
I = I0 − kt
R = 12,0 Ом I0 = 5,00 А I = 0
t = 2,00 с
Q1 = ? Q2 = ?
сывается в виде
Анализ и решение
Прохождение электрического тока по проводнику сопровождается выделением в нем тепла. При постоянном токе количество теплоты, выделившееся в проводнике, определяется по закону Джоуля– Ленца
Q = I 2 Rt .
Если сила тока в проводнике изменяется, то данный закон справедлив для бесконечно малого промежутка времени и запи-
dQ = I 2 Rdt , |
(1) |
где сила тока I является функцией времени. В данном случае
|
|
|
|
I = I0 − kt , |
|||
гдеk |
– |
коэффициент пропорциональности, равный отношению приращения силы |
|||||
тока |
I |
к интервалу времени t , за который произошло это приращение |
|||||
|
|
|
|
k = |
I . |
||
|
|
|
|
|
|
t |
|
Для нашего случая |
|
5,00 − 0 |
|
||||
|
|
k = |
I0 − I |
= k = |
= 2,50 А/с. |
||
|
|
|
|||||
|
|
|
t |
|
|
2,00 |
|
Подставим зависимость силы тока от времени в формулу (1) dQ = (I0 − kt)2 Rdt .
Для определения количества теплоты, выделившегося за данный промежуток времени, проинтегрируем полученное выражение в пределах от t1 до t2
Q = t2 |
(I0 |
- kt)2 Rdt = - |
|
R |
t2 |
(I0 - kt)2 d (I0 |
- kt) = - |
R |
× |
(I0 - kt)3 |
|
t2 . |
||||
|
|
|||||||||||||||
|
k |
k |
|
|||||||||||||
∫ |
|
|
|
|
∫ |
|
|
|
|
|
3 |
|
|
|||
t |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|||
Или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = - |
R |
(I |
|
- kt )3 - (I |
|
- kt )3 . |
(2) |
|||||||
|
|
|
|
|
||||||||||||
|
|
|
3k |
|
0 |
2 |
0 |
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Проверим наименование единицы измерения теплоты в системе СИ
н.е.и. Q = Ом× с × А3 = В× с × А2 = В× с× Кл = В× Кл = Дж . А А с
При определении количества теплоты, выделившегося за первую секунду пределы интегрирования в формуле (2) t1 = 0, t2 = 1 c и, следовательно
Q = - |
12,0 |
(5,00 - 2,50 ×1,00)3 - (5,00 - 2,50 × 0)3 |
=175 Дж. |
|||||
|
||||||||
|
1 |
|
3 × 2,50 |
|
|
|
||
|
|
|
|
|||||
За вторую секунду пределы интегрирования в формуле (2) t1 |
= 1 с, t2 = 2 c и, сле- |
|||||||
довательно |
|
|
|
|
|
|
|
|
Q = - |
12,0 |
(5,00 - 2,50 × 2,00)3 |
- (5,00 - 2,50 ×1,00)3 |
= 25,0 Дж. |
||||
|
||||||||
2 |
3 |
× 2,50 |
|
|
|
|
||
|
|
|
||||||
52

Найдем требуемое отношение количеств теплоты
Q2 = 25 = 1 .
Q1 175 7
Таким образом, за вторую секунду выделится теплоты в 7 раз меньше, чем за первую секунду.
Ответ: за первую секунду в проводнике выделилось Q1 = 25 Дж, за вторую секунду Q2 = 175 Дж. Соответствующее отношение количеств теплоты – 1/7.
ЗАДАЧИ
241. Сила тока в проводнике уменьшается по закону I (t) = I0e−at , где I0 = = 10 А, a = 0,1 с–1 . Определить заряд Q , прошедший в проводнике в интервале времени от t1 = 2 c, до t2 = 5 c.
242.Сила тока в проводнике равномерно увеличивается от I0 = 0 до некоторого максимального значения Imax в течение времени τ = 15 c. За это время в проводнике выделилось количество теплоты Q = 1 кДж. Определить скорость нарастания тока dI dt в проводнике, если сопротивление его R = 3 Ом.
dt в проводнике, если сопротивление его R = 3 Ом.
243.На участке цепи сопротивлением R = 3 Ом напряжение изменяется по закону U (t) = U0 /(1 + αt) , где U0 = 12 В, a = 1,5 с–1 . Определить заряд Q , прошед-
ший по проводнику в интервале времени от t1 = 0 c, до t2 = 2 c.
244.К источнику тока с э.д.с. ε = 1,5 В присоединили сопротивление R =
=0,1 Ом. Амперметр показал силу тока I1 = 0,5 А. Когда к источнику тока присое-
динили последовательно еще один источник тока с такой же э.д.с, то cила тока в том же сопротивление стала I2 = 0,4 А. Определить внутренние сопротивления r1 и r2 первого и второго источников тока.
245. Ток в проводнике изменяется со временем t по уравнению I (t) = (2 + 12 t)2 ,
где I измеряется в амперах, t – в секундах. Какой заряд Q проходит через поперечное сечение проводника за время от t1 = 0,5 с до t2 = 2,5 с? При каком постоянном токе I0 через поперечное сечение проводника за то же время проходит такой же заряд?
246. Имеется N одинаковых гальванических элементов с э.д.c. ε и внутренним сопротивлением r каждый. Из этих элементов требуется собрать батарею, состоящую из нескольких параллельно соединенных групп, содержащих по n последовательно соединенных элементов. При каком значении n сила тока I во внешней цепи, имеющей сопротивление R , будет максимальной? Чему будет равно внутреннее сопротивление батареи RБ при этом значении n ?
53
247.Найти заряд Q , который прошел через поперечное сечение проводника в
интервале времени от t1 = 4 c, до t2 = 6 c, если в течении времени τ = 10 с сила тока в нем уменьшилась от I0 = 10 А до I1 = 5 А по линейному закону.
248.Сила тока в проводнике сопротивлением R = 12,5 Ом равномерно возрас-
тает от I0 |
= 0 до некоторого максимального значения Imax в течение времени τ |
= |
= 5 с. За |
это время в проводнике выделилось количество теплоты Q |
= |
= 7,5 кДж. Найти среднюю силу тока I в проводнике за этот промежуток времени.
249. К батарее аккумуляторов c э.д.с. ε = 8 В и внутренним сопротивлением r = 1 Ом, присоединен проводник. Определить: 1) сопротивление R проводника, при котором мощность, выделяемая в нем, максимальна; 2) мощность P , которая при этом выделяется в проводнике.
250. Сила тока в проводнике сопротивлением R = 100 Ом изменяется по закону I (t) = I0 (1 − e−at ) , где I0 = 5 А, a = 0,15 с–1 . Определить количество теплоты Q , выделившееся в проводнике в интервале времени от t1 = 1 c, до t2 = 3 c.
Тема 15. Магнитное поле в вакууме. Закон Био– Савара– Лапласа. Принцип суперпозиции магнитных полей. Индукция магнитного поля прямолинейного и кругового проводников с током
Пример решения задач
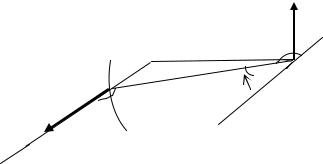
Проводник, по которому течет ток I = 5,00 А, имеет вид, показанный на рисунке. Радиус изогнутой части проводника R = 10,0 см, прямолинейные части проводника очень длинные. Определить индукцию магнитного поля созданного током в центре полукольца.
Дано |
|
|
|
|
|
|
|
|
|
I = 5,00 А |
|
|
Z |
|
|
|
|
|
|
R = 10,0 см |
|
|
|
I |
I |
|
|
|
|
B – ? |
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R |
2 |
|
I |
X |
|
|
|
|
О |
А |
|
||||
|
|
I |
B2 |
3 |
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
У 1 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
54
Анализ и решение
Для вычисления индукции магнитного поля воспользуемся законом Био– Савара– Лапласа и принципом суперпозиции магнитных полей. В силу этого принципа магнитная индукция B в любой точке магнитного поля проводника с током равна векторной сумме магнитных индукций dB , созданных в этой точке всеми его элементами Idl , то есть
В = ∫dB , |
(1) |
l |
|
где l означает, что интегрирование распространяется на всю длину проводника. Из принципа суперпозиции полей следует также, что если магнитное поле соз-
дано несколькими проводниками с током, то вектор B в какой-либо точке этого поля равен векторной сумме индукций магнитных полей, созданных в этой точке каждым током в отдельности
R N R |
|
B = ∑ Bi . |
(2) |
i=1
Чтобы получить правильный результат, применяя соотношения (1) и (2), необходимо знать направления складываемых векторов dB или Bi .
Разобьем проводник с током на три участка: два прямолинейных отрезка 1 и 3, ограниченных с одного конца, и полукольцо 2. Согласно (2), индукция магнитного поля в центре полукольца будет равна
BA = B1 + B2 + B3 .
Рассмотрим участок проводника 1 (см. рис. 2). Выделим на нем элемент тока
|
|
|
|
|
|
|
|
|
|
|
dB |
|
|
|
|
|
|
|
|
|
R |
|
α |
|
|
|
|
|
О |
|
|
|
|
|
А |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
dα |
|
||
Idl |
α |
|
|
|
|
r |
|
|
||||
N |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 2 |
|
|
|
|
|
|||
Idl и запишем закон Био– Савара– Лапласа в векторной форме |
|
|||||||||||
R |
|
|
μ |
0 |
I |
|
R |
R |
|
|
|
|
dB |
|
= |
|
|
|
dl |
r |
, |
|
|
(3) |
|
|
|
|
|
|
||||||||
1 |
|
4π r3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
здесь dB1 – индукция магнитного поля, |
создаваемая элементом провода dl |
с то- |
||||||||||
ком I в точке, определяемой радиус-вектором r , μ0 – магнитная постоянная, dl
– вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r – модуль радиуса-вектора r .
55
Как следует из (3), вектор dB1 перпендикулярен к плоскости, содержащей век-
торы dl и r . Направление dB1 можно найти по правилу правого винта: если поступательное движение винта совпадает с направлением тока в элементе, то направление вращения винта укажет направление вектора dB1 в данной точке.
Поскольку у нас проводник с током и точка A , в которой определяется B1, ле-
жат в одной плоскости, все элементарные векторы dB1 направлены вдоль одной прямой (см. рис. 1). Тогда выражение (1) можно переписать в скалярной форме.
В1 = |
∫ |
dB1 = |
∫ |
μ0I |
dl sinα , |
(4) |
|
4π r |
2 |
||||||
|
|
|
|
||||
|
l |
|
l |
|
|
|
|
где α – угол между векторами dl |
и r . |
|
|
|
|
|
|
Преобразуем подынтегральное выражение так, чтобы в нем была одна переменная, например, угол α . Из прямоугольного треугольника ОАС можно выразить модуль радиуса-вектора
r = |
R |
= |
R |
|
|
|
|
. |
(5) |
||
sin(π - α ) |
sinα |
||||
Для определения dl проведем дугу СД радиуса r с центром в точке A и найдем ее длину по формуле CД = r dα , где dα – центральный угол, лежащий напротив дуги. Так как участок провода с током CN = dl мал, то дугу можно заменить её хордой. Получившийся треугольник СДN можно считать прямоугольным и из него, с учетом (5), следует
dl = |
СД |
= |
r dα |
= |
r dα |
= |
R |
dα . |
|
sin(π − α ) |
sin(π − α ) |
sinα |
sin2 α |
||||||
|
|
|
|
|
Подставим в формулу (4) полученные значения r |
и |
dl |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
α2 μ0 I sin2 α R dα |
|
|
α2 μ0 I |
|
|
|
|
μ0 I |
|
α1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
B1 = |
|
|
|
|
|
|
|
sinα = |
|
|
sin |
α dα = |
|
|
(− cosα ) |
|
|
||||||
|
|
∫ 4π R2 sin2 α |
∫ |
|
|
|
α |
|
|||||||||||||||||
|
|
|
|
|
|
4π R |
|
|
|
|
4π R |
|
|
||||||||||||
|
|
|
α1 |
|
|
|
α1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Так как участок проводника ограничен с одной стороны, |
то угол α меняется от |
||||||||||||||||||||||||
α = π |
до α |
2 |
= π . В результате получим |
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ0I |
π |
|
|
|
|
μ0 I |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
B1 = |
− cosπ ) |
= |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
(cos |
2 |
|
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4π R |
|
|
|
4π R |
|
|
|
|
|
|
|||||
|
Рассмотрим участок проводника 3. Как следует из закона Био– Савара в ска- |
||||||||||||||||||||||||
лярной форме (4), угол, образованный любым элементом тока |
I dl и радиус- |
||||||||||||||||||||||||
вектором r , |
проведенным от |
элемента |
в точку |
A , равен π . |
Следовательно, |
||||||||||||||||||||
|
|
R |
|
и dB3 = 0 . Отсюда следует, что и B3 |
= 0 , то есть, участок 3 в точке |
||||||||||||||||||||
sin(dl ^ |
r ) = 0 |
||||||||||||||||||||||||
А магнитного поля не создает.
Рассмотрим участок проводника 2. Выделим на нем элемент тока I dl . Вектор dB2 , в соответствии с законом Био– Савара и правилом правого винта, в точке A будет перпендикулярен к плоскости чертежа и направлен к нам (см. рисунок).
56
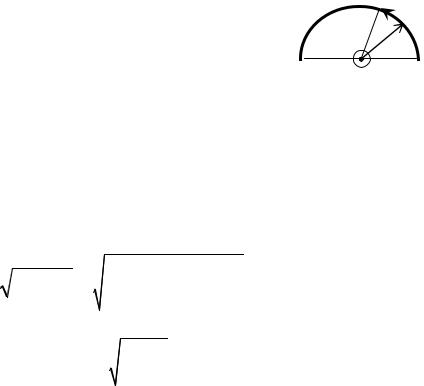
По причине, указанной выше, |
туда же будет направлен и вектор B2 (см. рис. 1). |
||||||||||||||||||||||||||
Угол, образованный элементом тока I dl |
|
и радиус-вектором |
|
|
|||||||||||||||||||||||
r , равен |
π |
|
|
|
|
R |
|
1 Тогда модуль |
2 |
dB2 |
|||||||||||||||||
. Следовательно, sin(dl ^ |
r ) = |
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
dB2 будет равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
dB2 |
||||
|
|
|
|
dB2 = |
|
0 |
I |
|
|
dl . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
4π R2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Согласно принципу суперпозиции, индукция B2 |
|
|
в точке A определяется интегри- |
||||||||||||||||||||||||
рованием |
B = π R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ0 I |
dl = |
|
|
μ0 I |
l |
|
|
π R = μ0 I . |
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 |
∫ |
4π R2 |
|
|
|
4π R2 |
|
0 |
|
|
4R |
|
|
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторы B1 и B2 взаимно перпендикулярны (см. рис. 1), следовательно |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
μ |
|
I |
|
2 |
|
|
|
μ |
|
I 2 |
|
|
|
||||
|
|
2 |
2 |
|
|
|
0 |
|
|
|
|
||||||||||||||||
|
B = |
B1 |
|
+ B2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
0 |
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
4π R |
|
|
|
4R |
|
|
|||||||||||||
Итак |
|
|
|
B = μ0 I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
+1 . |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
π 2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
4R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Проверим наименование единицы измерения индукции магнитного поля в системе СИ
н.е.и. B = |
Гн× А |
= |
Вб × А |
= |
Тл× м2 |
= Тл . |
|
м× м |
А× м× м |
м2 |
|||||
|
|
|
|
Подставим числовые значения физических величин и сделаем вычисления. Ответ: индукция магнитного поля в точке A равна 6,0·10–6 Тл.
ЗАДАЧИ
251. Тонкой ленте шириной l = 50 см, придали форму цилиндра радиуса R = = 20 см. По ленте течет равномерно распределенный по ее ширине ток силой I = 250 А. Найти напряженность магнитного поля H в точке A , расположенной на оси трубки в площади основания цилиндра.
252. Проводник, имеющий форму квадрата со стороной a = 20 см, находится в вакууме. По нему течет ток силой I = 15 А. Определить величину индукции магнитного поля B0 в точке пересечения диагоналей квадрата. Сравнить с величиной индукции магнитного поля B1 в центре кругового провода с таким же током, если его длина равна длине окружности, вписанной в квадрат.
253. В вакууме по двум бесконечно длинным прямым параллельным проводам, расположенным на расстоянии d = 20 см друг от друга, текут токи силой I1 = 50 А и
57

I2 = 100 А в противоположных направлениях. Определить индукцию магнитного поля B в точке A , удаленной на расстояние r1 = 25 см от первого и на r2 = 40 см от второго провода.
254. Два бесконечно длинных прямых провода в вакууме скрещены под прямым углом. По проводам текут токи силой I1 = 60 А и I2 = 80 А. Расстояние d между проводами равно 15 см. Определить индукцию магнитного поля B в точке A , одинаково удаленной от обоих проводников на расстояние r1 = r2 = 7,5 см.
255. По двум бесконечно длинным прямым параллельным проводам текут токи силой I1 = 20 А и I2 = 30 А в одном направлении. Расстояние d между проводами равно 10 см. Вычислить напряженность магнитного поля H в точке A , удаленной от обоих проводов на одинаковое расстояние r1 = r2 = 8 см.
256.Напряженность магнитного поля H1 в центре кругового витка (точка 1) радиусом R = 15 см равна 30 А/м. Определить напряженность H2 в точке 2, расположенной на оси витка на расстоянии d = 6 см от точки 1.
257.Тонкий прямой стержень длиной l = 20 cм согнут посередине под углом
α= 120°. По нему течет ток силой I = 50 А. Найти напряженность магнитного поля H в точке 1, лежащей на биссектрисе угла α и удаленной от его вершины на расстояние a = 5 см.
258.По контуру в виде ромба с длиной стороны a = 10 см и углом α = 60° идет ток силой I = 10 А. Определить напряженность магнитного поля H в точке пересечения диагоналей ромба.
259.Электрон в невозбужденном атоме водорода движется вокруг ядра по окружности радиусом r = 53 пм. Вычислить силу эквивалентного кругового тока I
инапряженность H поля в центре окружности.
260.По тонкому проволочному кольцу радиусом R течёт ток I . Не изменяя силы тока в проводнике, ему придали форму равностороннего треугольника. Во сколько раз изменилась индукция магнитного поля B0 в центре контура?
Тема 16. Магнитное поле в вакууме. Сила, действующая на проводник с током в магнитном поле (сила Ампера)
Пример решения задач
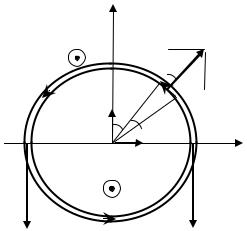
Проводящее кольцо поместили в однородное магнитное поле. По кольцу циркулирует ток I = 40,0 А. Если проволока кольца выдерживает на разрыв нагрузку F = 15,0 Н, то при какой индукции магнитного поля В кольцо разорвется? Радиус кольца R = 20,0 см, его плоскость перпендикулярна линиям магнитной индукции.
58
Дано |
|
У |
|
|
|
|
I = 40,0 А |
|
|
|
|
|
|
F = 15,0 Н |
|
|
dFAу |
|
|
dFА |
R = 20,0 см |
|
B |
|
|
||
|
|
|||||
|
|
|
|
|||
B = ? |
|
|
|
|
i |
|
|
|
|
|
|
||
|
I |
У |
|
|
|
|
|
|
|
|
|||
|
ϕ |
dFAх |
||||
|
|
RjОi |
d β dϕR |
|
Х |
|
|
|
O |
j β |
|
|
|
|
|
i |
|
|
||
|
|
B |
|
|
||
|
|
|
|
|
|
|
|
F |
|
I |
F1упр |
||
|
упр |
|
|
|||
2 |
|
|
|
|
||
Анализ и решение
На каждый элемент кольца dl , по которому течет ток, со стороны магнитного поля действует сила dFA (сила Ампера). Величина и направление этой силы определяется по закону Ампера
R |
RR |
(1) |
|
dF = I dlB . |
|||
A |
|
|
|
R |
R |
π . Поэтому в скалярной форме урав- |
|
По условию во всех точках кольца (dl ^ B) = |
|||
нение (1) имеет вид |
|
2 |
|
|
R |
|
|
|
|
|
|
dFA = IdlB sin(dl ^ B) = IdlB . |
(2) |
||
Если ток в кольце течет против хода часовой стрелки, а вектор внешнего магнитного поля направлен на нас (см. рисунок), то силы dFA , действующие на все элементы кольца, лежат в одной плоскости (в плоскости рисунка), направлены по радиусам кольца и стремятся растянуть его. В результате, внутри сечения кольца возникает упругая сила, препятствующая растяжению. Чтобы определить эту силу, надо из кольца вырезать элемент и приложить к разрезам силы со стороны остальной части кольца. Так как кольцо находится в равновесии, то и выделенный элемент под действием всех сил, приложенных к нему, так же будет находиться в равновесии.
В качестве элемента удобно взять верхнюю половину кольца. К местам разреза приложим силы F1упр и F2 упр , которые действуют со стороны нижней половины кольца. Так как верхняя половина кольца должна находится в равновесии, то
FA + F1упр + F2 упр = 0 , |
(3) |
здесь FA – сила Ампера, действующая на полукольцо с током со стороны внешнего магнитного поля. Если эта сила будет больше сил упругости, то кольцо с током
59
