
ОГЛАВЛЕНИЕ
|
ЗАДАЧА 18…………...………................................................................ |
3 |
|
ЗАДАЧА 22……………………………………………………………... |
9 |
|
ЗАДАЧА 23…………………………………………………………..…. |
16 |
|
ЗАДАЧА 39……………………………………………..………………. |
24 |
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………..………... |
28 |
ЗАДАЧА 18
Для консольного бруса переменного сечения (рисунок 18) построить эпюры нормальной силы, наибольших нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки Р и при найденном значении нагрузки вычислить наибольшее перемещение, а также удлинение участка а. Принять F = А = 2 см2, l = 20 см, k = 2, остальные данные взять из таблицы 18 и таблицы 41.

Рисунок 18
Таблица 18
|
Цифра варианта |
Порядковый номер цифры в варианте |
||||||||||
|
1 |
2 |
3 |
4 |
||||||||
|
А1/А |
b/1 |
P1/P |
c/1 |
P2/P |
Материал |
№ схемы |
a/l |
P3/P |
|||
|
1 2 3 4 5 6 7 8 9 0 |
1,2 1,7 1,5 2,0 1,3 1,4 1,8 1,6 1,9 2,0 |
1,0 1,5 2,0 2,5 1,0 1,5 1,5 1,0 1,5 2,0 |
1 2 -2 1 1 -1 -1 -2 -1 2 |
1,5 1,5 1,0 1,0 2,5 1,5 2,0 2,0 1,0 1,5 |
-4 3 4 -3 3 -3 -3 3 -4 -4 |
Сталь 20 Ст. 4 Сталь 45 Сталь 20ХН Алюм. спл. АЛ-4 Сталь 40Х Алюм. спл. АК-4 Титан. спл. ВТ-3 Магн. спл. МА-5 Латунь Л-68
|
I II III IV V I II III IV V |
2,5 2,0 2,5 2,0 1,5 2,0 2,5 1,5 2,0 1,0 |
2,5 1,5 -1,0 -2,0 -1,5 2,0 1,0 -2,5 -1,0 1,0 |
||
Таблица 41 – Механические характеристики материалов
|
|||||||||||||
|
Материал |
Марка |
Т, МПа |
В, МПа |
Т, МПа |
Е 10-5, МПа |
|
|||||||
|
Ст. 3 Ст. 4 Ст. 5 20 40 45
|
230 240 280 220 320 320
|
380 470 430 550 520 650 400 500 650 600 750 |
160 170 190 160 220 220 |
2,0 |
0,28 |
|||||||
|
20ХН 40Х 40ХН 12ХН3А |
600 800 750 700 |
800 1000 900 950 |
350 440 390 400 |
2,1 |
0,30 |
|||||||
|
АЛ-4 АК-4 АД-16 |
200 310 330 |
260 400 470 |
120 180 200 |
0,72 |
0,30 |
|||||||
|
ВТ-3 |
950 |
1100 |
500 |
1,2 |
0,26 |
|||||||
|
Л-68 |
330 |
450 |
200 |
1,2 |
0,36 |
|||||||
|
МА-5 |
220 |
300 |
160 |
0,72 |
0,27 |
|||||||
|
|||||||||||||
|
Марка |
ВР, МПа |
ВС, МПа |
Е 10-5, МПа |
|
|||||||||
|
СЧ 12-28 СЧ 15-32 СЧ 18-36 СЧ 24-44 СЧ 35-56 |
120 150 180 240 350 |
500 600 670 800 900 |
1,2 |
0,25 |
|||||||||
Дано:
А1/А
= 1,2; b/l
= 1,5; P1/P
= -1; c/1
= 1,5; P2/P
= -4; материал: латунь Л-68; схема II;
a/l
= 2; P3/P
= 1,5; А = 2 см2;
l
= 20 см; k
= 2.
Требуется:
-
Построить эпюры N, , .
-
Определить Р.
-
Определить max и
 lа.
lа.
Решение
-
Изобразим расчетную схему бруса в соответствии с заданием и разобьем его на участки I, II, III, IV.
-
Применив метод сечений, определим продольные силы в сечениях каждого участка и построим их эпюру (ЭN):
участок I. N1 = P;
участок II. N2 = N1 = P;
участок III. N3 = P + 4P = 3P;
участок IV. N4 = P + 4P 1,5P = 1,5P.
-
Найдем нормальные напряжения в сечениях бруса
 по участкам:
по участкам:
 ;
;
 ;
;
 ;
;
 .
.
Строим
эпюру напряжений (Э),
в долях
 .
.
-
Определим удлинения (укорочения) участков бруса
 :
:
 ;
;
 ;
;
 ;
;

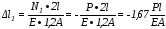 .
.
-
Определение перемещений начинаем от защемленного конца бруса.
Перемещение сечения «К»: К = 0.
Перемещение
сечения «Е»:
 .
.
Перемещение
сечения «Д»:
 .
.
Перемещение
сечения «С»:
 .
.
Перемещение
свободного конца бруса (сечение «В»):
 .
.
По
полученным результатам строим эпюру
перемещений (Э)
в долях
 .
.
-
Определение допускаемой нагрузки Р из условия прочности max , где
 (из эпюры )
(из эпюры )

 .
.
Для
латуни Л-68 предел текучести Т
=
330 МПа:  МПа.
МПа.
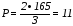 кН.
кН.
Принимаем Р = 11 кН.
-
При найденном значении нагрузки определим укорочение участка «а».
Для латуни Л-68: Е = 1,2 105 МПа.
 мм
знак «»
указывает на укорочение.
мм
знак «»
указывает на укорочение.
Максимальное перемещение:
 или
или
 мм.
мм.
Ответ:
Р
= 11 кН; max
= 0,527 мм;
 мм.
мм.
ЗАДАЧА 22
К стальному брусу переменного сечения (рисунок 22) приложены скручивающие моменты М1 и М2. Определить размера бруса исходя из того, что должны удовлетворяться условия прочности и жесткости. При найденных размерах вычислите (в градусах) максимальный угол поворота поперечных сечений.
Принять: l = 20 см, М = 500 Нм, = 80 МПа, = 4,0 град/м, G = 8 104 МПа. Остальные значения взять из таблицы 22.

Рисунок 22
Таблица 22
|
Цифра варианта |
Порядковый номер цифры в варианте |
|||||||
|
1 |
2 |
3 |
4 |
|||||
|
e/l |
a/b |
№ схемы |
c/l |
M1/M |
d/D |
M2/M |
||
|
1 2 3 4 5 6 7 8 9 0 |
4,0 3,5 3,0 2,5 2,0 1,5 2,0 2,5 3,0 3,0 |
1,00 2,00 1,50 1,50 1,75 1,00 2,00 1,50 1,75 2,00 |
I II I II I II I II I II |
1,5 2,0 2,0 2,0 2,5 3,0 2,5 2,5 2,0 2,0
|
1 -1 2 1 -2 -1 2 -1 2 1 |
0,65 0,85 0,70 0,80 0,75 0,80 0,70 0,65 0,75 0,85 |
-3,0 -2,5 3,0 -1,5 -2,7 2,8 -3,2 2,6 3,4 -2,2 |
|
Дано:
e/l
= 4; a/b
= 2; схема II;
c/l
= 2; M1/M
= 1; d/D
= 0,85; M2/M
= -2,5; l
= 20 см; М = 500 Нм;
= 80 МПа;
= 4,0 град/м; G
= 8
104
МПа.
Требуется:
-
Определить размеры сечений бруса
удовлетворяющих прочности жесткости.
-
Определить max.
Решение
-
Изобразим расчетную схему бруса в соответствии с заданием и выразим размеры сечений через параметр D: d = 0,85D; а = D;
 .
. -
Разобьем брус на участки I, II, III и, применив метод сечений, определим крутящие моменты T в сечениях каждого участка:
участок I. Т1 = М;
участок II. Т2 = М + 2,5М = 1,5 М;
участок III. Т3 = Т2 = 1,5М.
Строим эпюру крутящихся моментов (ЭТ).
-

-
Определим геометрические характеристики прочности и жесткости сечений.
-
3.1) Кольцевое сечение:
-
Wk =
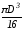
1-
1-
=
=
1
(0,85)4
= 0,094D3;
1
(0,85)4
= 0,094D3; -
Ik =
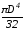
1-
1-
=
=

1
(0,85)4
= 0,047D4.
1
(0,85)4
= 0,047D4. -
3.2) Круглое сплошное сечение:
-
 ;
; -
 .
. -
3.3) Прямоугольное сечение:
-
 ,
при
,
при
 и
= 0,493
(из таблицы);
и
= 0,493
(из таблицы); -
 ;
; -
 ,
где l
= 0,457
(из таблицы);
,
где l
= 0,457
(из таблицы); -
 .
. -
Наибольшие касательные напряжения в сечениях бруса
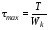 :
: -
участок I.
 ;
; -
участок II.
 ;
; -
участок III.
 .
. -
Строим эпюру касательных напряжений (Э) в долях
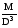 .
. -
Определение размеров сечений из условия прочности max , где
 (из эпюры )
(из эпюры )
 ,
откуда
,
откуда
 мм.
мм. -
Принимаем D = 54 мм, соответственно d = 0,85 54 = 46 мм.
-
а = D = 54 мм, b = 0,5D = 27 мм.
-
Относительные углы закручивания по участкам
 :
: -
 ;
; -
 ;
; -
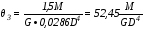 .
. -
Размеры сечений из условия жесткости max , где
 (из эпюры )
(из эпюры )
 ,
откуда параметр D
определяется:
,
откуда параметр D
определяется:
 ,
где
= 4 град/м
или
,
где
= 4 град/м
или
 рад/м
= =
0,698
10-4
рад/мм.
рад/м
= =
0,698
10-4
рад/мм. -
После подстановки числовых значений получим:
-
 мм.
мм. -
Принимаем D = 48 мм. Соответственно, а = D = 48 мм, b = 0,5а = 24 мм, d = = 0,85 48 = 40 мм.
-
Размеры, полученные из условия жесткости меньше размеров, полученных в пункте 5. Следовательно, эти размеры условию прочности не удовлетворяют.
-
Окончательно принимаем размеры из условия прочности:
-
D = 54 мм, а = 54 мм, b = 27 мм, d= 46 мм.
-
Относительные углы поворота сечений =
 :
: -
b-a =
 =
52,45
=
52,45
 ;
; -
c-b =
 =
60
=
60
 ;
; -
d-c =
 =
42,55
=
42,55
 .
. -
Определение углов поворота сечений начинаем от защемленного конца бруса:
-
угол поворота сечения «а»: а = 0;
-
угол поворота сечения «b»: b = а + b-а = 0 +
 =
=
 ;
; -
угол поворота сечения «с»: с = b + с-b =
 ;
; -
угол поворота сечения «d»: d = c + d-c =

-
По полученным результатам строим эпюру относительных углов поворота сечения (Э) в долях
 .
. -
Наибольший угол поворота сечения:
-
max = с =
 или max
=
или max
= рад,
рад,
-
или max =
 .
. -
Ответ: размеры сечений бруса удовлетворяющих прочности и жесткости: D = 54 мм, а = 54 мм, b = 27 мм, d = 46 мм; max
 .
. -
Задача 23
-
Для стальной балки, изображенной на рисунке 23а, требуется:
-
Подобрать из расчета на прочность по наибольшим напряжениям размеры сечения трех типов:
-
тип I – двутавр либо сечение, составленное из двух швеллеров или двутавров (рисунок 23б);
-
тип II прямоугольное сечение с отношением высоты к основанию h/b равным отношению для сечения I типа;
-
тип III круглое (сплошное) сечение.
-
Вычертить найденные сечения в одном масштабе и сравнить веса соответствующих балок (подсчитать отношение площадей сечений).
-
В сечении балки с наибольшей поперечной силой для каждого типа сечения вычислить наибольшие касательные напряжения.
-
Принять: q = 50 кН/м, l = 40 см, материал СТ. 5, k = 1,6, остальные данные взять из таблиц 23 и 41.

-
Рисунок 23
-
-
-
Таблица 23
-
Цифра варианта
-
Порядковый номер цифры в варианте
-
1
-
2
-
3
-
4
-
l1/l
-
l2/l
-
P2/ql
-
Тип сечения
-
P1/ql
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
0
-
1,0
-
1,5
-
2,0
-
2,5
-
3,0
-
3,0
-
2,5
-
2,0
-
1,5
-
1,0
-
2,0
-
2,5
-
1,5
-
1,0
-
1,0
-
1,5
-
2,0
-
2,5
-
1,0
-
2,0
-
4
-
3
-
2
-
-2
-
-3
-
-4
-
2
-
-2
-
-3
-
3
-
I
-
II
-
III
-
IV
-
I
-
II
-
III
-
IV
-
I
-
II
-
1
-
-1
-
-2
-
2
-
3
-
-3
-
4
-
-4
-
2
-
-2
-
-
Дано: l1/l =1; l2/l = 2; P2/ql =3; сечение II; P1/ql = -1; q = 50 кН/м; l = 40 см; материал СТ. 5; k = 1,6.

-
Требуется:
-
Из расчета на прочность подобрать сечения трех типов сдвоенный швеллер, прямоу-гольник, круг.
-
Сравнить веса полученных балок.
-
Определить max.
-
Решение
-
Изобразим расчетную схему балки в соответствии с условием задачи и определим опорные реакции:
-
 RA
4l + ql
3l + 3ql
1,5l
3ql
2l = 0;
RA
4l + ql
3l + 3ql
1,5l
3ql
2l = 0;
-
 RB
4l + 3ql
(l + 1,5l) + 3ql
2l
ql2
= 0
RB
4l + 3ql
(l + 1,5l) + 3ql
2l
ql2
= 0
-
 ;
; -
 .
. -
Проверка:
-
 ;
0,375ql
ql
3ql + 3ql + 0,625ql = (4
4)
ql = 0.
;
0,375ql
ql
3ql + 3ql + 0,625ql = (4
4)
ql = 0.
-
Разобьем балку на участки I, II, III и, применив метод сечений, определим поперечные силы Qу и изгибающие моменты Мх в сечениях каждого участка. По полученным результатам строим эпюры.
-
2.1) Построению эпюры Qу.
-
Участок I. Сечение 1 1 (0 Z1 l).
-
Qy = 0,375ql = const.
-
Эпюра параллельна оси.
-
Участок II. Сечение 2 2 (2l Z2 3l).
-
Qy = -0,625ql + qZ2 3ql = qZ2 3,625ql уравнение прямой.
-
Поперечная сила на участке изменяется по линейному закону.
-
При Z2 = 3l: Qy = 3ql 3,625ql = -0,625ql.
-
При Z2 = 2l: Qy = 2ql 3,625ql = -1,625ql.
-
Участок III. Сечение 3 3 (0 Z3 2l).
-
Qy = 0,625ql + qZ3 уравнение прямой.
-
Поперечная сила изменяется по линейному закону.
-
При Z3 = 2l: Qy = -0,625ql + 2ql = 1,375ql.
-
При Z3 = 0: Qy = -0,625ql.
-
Поперечная сила на участке меняет знак с «+» на «», следовательно, на эпюре Мх ожидается точка «max».
-
Определим Z3, при котором Qy = 0, т.е., -0,625ql + qZ3 = 0

-
2.2) Построение эпюры Мх.
-
Сечение 1 1 (0 Z l).
-

-
Мх = 0,375ql Z уравнение прямой.
-
Изгибающий момент на участке изменяется по линейному закону.
-
При Z1 = 0: Мх = 0; при Z1 = l: Мх = 0,375ql2.
-
Сечение 2 2 (2l Z2 3l).
-
 или
после преобразований:
или
после преобразований:

-
Изгибающий момент изменяется по закону квадратной параболы.
-
При Z2 = 3l:
 .
. -
При Z2 = 2l:
 .
. -
Сечение 3 3 (0 Z3 2l).
-

уравнение
параболы.
уравнение
параболы.
-
При Z3 = 2l:

-
При Z3 = 0: Мх = 0.
-
При Z3 = 0,625l точка «max».
-

-
Эпюра Мх построена на растянутых волокнах.
-
Расчетный момент сопротивления сечения балки из условия прочности:
 ,
где Мxmax
= 0,75ql2
(из эпюры Мх)
,
где Мxmax
= 0,75ql2
(из эпюры Мх)
 ,
расчетный момент сопротивления
,
расчетный момент сопротивления
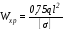 ,
где q
= 50 кН/м = 50 Н/мм;
,
где q
= 50 кН/м = 50 Н/мм;
 .
.
-
Для стали Ст.5 предел текучести т = 280 МПа:
 МПа.
МПа. -
После подстановки числовых значений расчетный момент сопротивления определится:
 см3.
см3.
-
Подбор сечений.
-
4.1) Так, как балка составлена из двух швеллеров, то момент сопротивления швеллера определится:
 см3.
см3.
-
По таблицам сортамента (ГОСТ 8240 72) принимаем швеллер № 8, для которого: Wx = 22,4 см3, Ix = 89,4 см4, Sx = 13,3 см3, А = 8,98 см2, h = 80 мм, b = 40 мм, d = 4,5 мм.
-
Площадь сечения балки: Асеч = 2 А = 2 8,98 = 17,96 см2.
-
4.2) Для прямоугольного сечения:
 .
. -
Принимаем отношение
 как у швеллера, т.е.
как у швеллера, т.е.
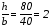 ,
т.е. h
= 2b
,
т.е. h
= 2b

 см.
см. -
h = 2b = 2 3,72 = 7,44 см.
-
Окончательно принимаем прямоугольное сечение с размерами сторон h x b = = 75 х 38 мм.
-
Площадь сечения: Асеч = b h = 3,8 7,5 = 28,5 см2.
-
4.3) Для круглого сплошного сечения:
-

 см.
см. -
Принимаем круглое сечение диаметром d = 70 мм.
-
Площадь сечения:
 см2.
см2.
-
Изобразим сечения балки в одном масштабе и сравним веса полученных балок.
-
Масштаб: 1:2
-

-
Веса полученных балок сравним по отношению их площадей поперечных сечений. Для наглядности составим сравнительную таблицу:
-
-
Наименование профиля
-
Сдвоенный швеллер
-
Прямоугольник
-
Круг
-
Площадь сечения, см2
-
17,96
-
28,5
-
38,46
-
Отношение

-
1
-
1,59
-
2,14
-
-
Как видно из таблицы самой легкой является балка, составленная из двух швеллеров, самой тяжелой балка круглого сечения.
-
Определение наибольших касательных напряжений.
