Задача 6

1. Найдите уравнение регрессии y=a₀+a₁x зависимости выработки Y от стажа Х.

2. Определите коэффициент корреляции R. Оцените направление и тесноту связи, значимость коэффициента корреляции с помощью критерия Стьюдента на уровне значимости α = 0,05.

3. Постройте точки М_i(x_i, y_i) и теоретическую линию регрессии.

4. Оцените надежность уравнения регрессии с помощью критерия Фишера на уровне значимости α = 0,05.

5. Рассчитайте прогноз Y при Х = 10,7 лет.

Таблица 7  Выработка деталей в зависимости от стажа работы

№	Стаж работы Х, лет	Выработка деталей Y, шт.
1	1,7	2
2	2,7	4
3	4,7	5
4	5,7	5
5	6,7	7
6	7,8	6
7	9,7	7

Решение

1. Составим расчетную таблицу.

Таблица 8  Расчетная таблица

i	xi	yi	xiyi
1	1,7	2	3,4	2,89	4
2	2,7	4	10,8	7,29	16
3	4,7	5	23,5	22,09	25
4	5,7	5	28,5	32,49	25
5	6,7	7	46,9	44,89	49
6	7,7	6	46,2	59,29	36
7	9,7	7	67,9	94,09	49
	38,9	36	227,2	263,03	204

Уравнение регрессии y=a₀+a₁x.

Для нахождения коэффициентов решим систему уравнений:

7а₀ + 38,9а₁ = 36  38,9

38,9а₀ + 263,03а₁ = 227,2  7

 272,3а₀ + 1513,21а₁ = 1400,4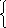

272,3а₀ + 1841,21а₁ = 1590,4

-328а₁ = -190

а₁  0,579

7а₀ + 38,9а₁ = 36

7а₀ + 38,9  0,579 = 36

7а₀ = 36  22,5231

7а₀ = 13,4769

а₀ = 1,925

у = 1,925 + 0,579х  уравнение регрессии

2. Коэффициент корреляции: .

Найдем выборочные средние и средние квадратические отклонения:

;

;

;

;

;

;

.

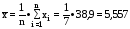Коэффициент корреляции: .

Т.к. R  0, то связь прямая  с увеличением стажа работы Х выработка У увеличивается, т.к. R  0,9, то теснота связи очень высокая, т.е. выработка существенно зависит от стажа работы.

Оценим значимость коэффициента корреляции на уровне значимости α = 0,05.

Найдем значение критерия Стьюдента:

, где n = 7, R_xy = 0,913.

.

Найдем табличное значение критерия. Число степеней свободы: k = n  2 =

= 7  2 = 5.

По таблице находим критическую точку: t_кр = t (α=0,05; k = 5) = 2,12.

Т.к.  t_кр, то коэффициент корреляции является значимым. С вероятностью р = 1  0,05 = 0,95 можно утверждать, что случайные величины х и у во всей генеральной совокупности, из которой отобраны значения x_i, у_i связаны корреляционной зависимостью, т.е. коэффициент корреляции R  0.

3. Построим точки М_i(x_i, y_i) и линию регрессии у = 1,925 + 0,579х.

х	5	10
у	4,82	7,72

Точки располагаются вблизи от линии регрессии, что говорит о высокой точности построенной модели (уравнение регрессии).

4. Оценим надежность, достоверность уравнения на уровне значимости 0,05. Применим критерий Фишера:

где R² =0,913; n  m  1 = 7  1  1 =5; m = 1.

По таблице находим F_табл = 6,61.

Т.к. F  F_табл, то уравнение регрессии является статистически надежным.

5. Прогноз при Х = 10,7 лет:

У(10,7) = 1,925 + 0,579  10,7 = 8,1203  8 шт.

ЗАДАЧА 9

Имеется m пунктов А₁,А₂, ..., Аm поставщиков груза и n пунктов B₁,B₂, ..., B_n

потребления груза; a_i т - запас груза в пункте А_i, b_j т  потребность груза в пункте B_j. Известна матрица затрат C=(С_ij) в руб. на перевозку 1 т груза из пункта А_i в пункт B_j.

Найти оптимальный план перевозок.

Исходные данные: a₁=50, a₂=87, a₃=70, b₁=35, b₂=62, b₃=50, b₄=60, .

Решение

Проверим замкнутость системы а_i = b_i:

a_i = 50 + 87 + 70 = 207;

b_i = 35 + 62 + 50 + 60 = 207.

Система замкнута.

Заполним таблицу.

Таблица 9

	В1	В2	В3	В4	аi
А1	 5	50 2	 5	 3	50
А2	35 4	12 3	 7	40 4	87
А3	 5	 5	50 2	20 6	70
bi	35	62	50	60	207

Начнем с 1-ого столбца. Наименьшая стоимость перевозки 4 руб.

х₂₁ = min 81; 35 = 35. Первый столбец закрыт.

Переходим ко 2-му столбцу.

х₁₂ = min 50; 62 = 50. Первая строка закрыта.

х₂₂ = min 62  50; 87  35 = 12. Второй столбец закрыт.

х₃₃ = min 70; 50 = 50. Третий столбец закрыт.

х₂₄ = min 87  35  12; 60 = 40

х₃₄ = min 70  50; 60  40 = 20

Остатки по строке и столбцу равны 0, опорное исходное решение построено. Этому плану соответствуют затраты:

F = 50  2 + 35  4 + 12  3 + 40  4 + 50  2 + 20  6 = 100 + 140 + 36 + 160 + 100 + 120 = 656 руб.

Вычислим потенциал:

₁ + ₂ = 2

₂ + ₁ = 4

₂ + ₂ = 3

₂ + ₄ = 4

₃ + ₃ = 2

₃ + ₄ = 6

Возьмем: ₁ = 0, ₂ = 1, ₃ = 3; ₁ = 3, ₂ = 2, ₃ = -1, ₄ = 3.

₁₁ = 5  ₁  ₁ = 5  0  3 = 2

₁₃ = 5  ₁  ₃ = 5  0  (-1) = 6

₁₄ = 3  ₁  ₄ = 3  0  3 = 0

₂₃ = 7  ₂  ₃ = 7  1  (-1) = 7

₃₁ = 5  ₃  ₁ = 5  3  3 = -1

₃₂ = 5  ₃  ₂ = 5  3  2 = 0

Т.к. ₃₁  0 составим цикл пересчета и произведем сдвиг по этому циклу:

Получим:

15⁴  60⁴

20⁵ 0⁶

Рассмотрим новое решение.

Таблица 10

	В1	В2	В3	В4	аi
А1	 5	50 2	 5	 3	50
А2	15 4	12 3	 7	60 4	87
А3	20 5	 5	50 2	 6	70
bi	35	62	50	60	207

Затраты:

F₁ = 50  2 + 15  4 + 12  3 + 60  4 + 20  5 + 50  2 = 100 + 60 + 36 + 240 + 100 + 100 = 636 руб.

F  F₁ = 656  636 = 20 руб.План улучшится на 20 рублей.

Вычислим потенциал:

₁ + ₂ = 2

₂ + ₁ = 4

₂ + ₂ = 3

₂ + ₄ = 4

₃ + ₁ = 5

₃ + ₃ = 2

Возьмем: ₁ = 0, ₂ = 1, ₃ = 2; ₁ = 3, ₂ = 2, ₃ = 0, ₄ = 3.

₁₁ = 5  ₁  ₁ = 5  0  3 = 2

₁₃ = 5  ₁  ₃ = 5  0  0 = 5

₁₄ = 3  ₁  ₄ = 3  0  3 = 0

₂₃ = 7  ₂  ₃ = 7  1  0 = 6

₃₂ = 5  ₃  ₂ = 5  2  2 = 1

₃₄ = 6  ₃  ₄ = 6  2  3 = 1

Т.к. все _ij  0, то оптимальное решение найдено.