Министерство образования и науки Российской Федерации

ФГБОУ ВПО «Южно-Уральский государственный университет» (НИУ)

Филиал ФГБОУ ВПО «ЮУрГУ» (НИУ) в г. Сатке

Кафедра гуманитарных и социально-экономических наук

Дисциплина Математические методы и модели в экономике

КОНТРОЛЬНАЯ РАБОТА

7 Вариант

Студентка Зыкова Н.Л.

Группа СтЭЗ – 387

Преподаватель Шайкина В.Н.

Сатка 2013

ОГЛАВЛЕНИЕ

ЗАДАЧА 1…………...………..................................................................	3
ЗАДАЧА 5………………………………………………………..……...	10
ЗАДАЧА 6……………………………………………………………….	13
ЗАДАЧА 9……………………………………………………………….	17
БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………..………...	19

ЗАДАЧА 1

Дана матрица планирования производства изделий А, В.

Постройте оптимальный план выпуска продукции, обеспечивающий

максимальную стоимость продукции.

1. Решите задачу графическим методом, в MS Excel.

2. Решите задачу симплексным методом.

3. Запишите двойственную задачу, найдите ее решение.

4. Определите ценность ресурсов.

5. Оцените стоимость, если ресурсы сырья каждого вида увеличились на 50 кг.

6. Определите целесообразность включения в план нового изделия С, если нормы расхода сырья 3, 5, 4 кг, а стоимость одного изделия 80 руб.

Таблица 1  Матрица планирования производства

Вид сырья	Затраты сырья вида i на изготовление единицы продукции j		Запасы сырья Pi
	A	B
1	2	7	560
2	3	3	300
3	5	1	339
Стоимость, руб.	62	42

Решение

Составим систему неравенств:

2х₁ + 7х₂  560

3х₁ + 3х₂  300

5х₁ + х₂  339

х₁  0, х₂  0

z = 62х₁ + 42х₂  функция прибыли.

1. Заменим знаки неравенств на знаки равенств.

2х₁ + 7х₂ = 560 7х₂ = 560  2х₁ х₂ = 80  х₁

3х₁ + 3х₂ = 300 3х₂ = 300  3х₁ х₂ = 100  х₁

5х₁ + х₂ = 339 х₂ = 339  5х₁ х₂ = 339  5х₁

х₂ = 80  х₁

х1	70	0
х2	60	80

х₂ = 100  х₁

х1	70	80
х2	30	20

х₂ = 339  5х₁

х1	50	60
х2	89	39

Многоугольник ОАВСД – область решения неравенств. Построим вектор 62; 42. Опорная прямая при выходе из многоугольника ОАВСД пройдет через точку С. Найдем ее координаты:

5х₁ + х₂ = 339  5х₁ + х₂ = 339

3х₁ + 3х₂ = 300 : 3 х₁ + х₂ = 100

4х₁ = 239

х₁ = 59,75

х₂ = 100  х₁ = 100  59,75 = 40,25

С (59,75; 40,25).

В точке С функция максимизируется, поэтому максимальная прибыль:

z_max = 62  59,75 + 42  40,25 = 5395 руб.

2. Симплексный метод.

Запишем задачу в каноническом виде, введя дополнительные переменные х₃, х₄, х₅.

2х₁ + 7х₂ + х₃ = 560

3х₁ + 3х₂ + х₄ = 300

5х₁ + х₂ + х₅ = 339

х₁  0, х₂  0, х₃  0, х₄  0, х₅  0

Функцию z представим в неявном виде: z  62х₁  42х₂ = 0.

Составим симплекс  таблицу.

Таблица 2  Симплекс  таблица

	х1	х2	х3	х4	х5	b
х3	2	7	1	0	0	560	= 280
х4	3	3	0	1	0	300	= 100
х5	5	1	0	0	1	339	= 67,8
z	-62	-42	0	0	0	0

ведущая строка

ведущий столбец

Составим новые таблицы.

Таблица 3  Симплекс  таблица 2

	х1	х2	х3	х4	х5	b
х3	0		1	0	-	424,4
х4	0		0	1	-	96,6	ведущая строка
х1	1		0	0		67,8
z	0	-	0	0		4203,6

ведущий столбец

Таблица 4  Симплекс  таблица 3

	х1	х2	х3	х4	х5	b
х3	0	0	1	-		158,75
х2	0	1	0		-	40,25
х1	1	0	0	-		59,75
z	0	0	0			5395

В последней строке таблицы все числа неотрицательные. Следовательно, примем к оптимальному решению, которому будет базисное решение: х₁ = 59,75; х₂ = 40,25; х₃ = 158,75; переменные х₄, х₅ являются свободными и равны 0: х₄ = 0; х₅ = 0.

Прибыль составит: z = 5395 руб.

3. Двойственная задача.

z = 560у₁ + 300у₂ + 339у₃  max.

2у₁ + 3у₂ + 5у₃  62

7у₁ + 3у₂ + у₃  42

у₁  0, у₂  0, у₃  0

Решением исходной задачи является план:

(2  59,75 + 7  40,25  560)  =0 -158,75 = 0

(3  59,75 + 3  40,25  300)  =0 0=0

(5  59,75 + 40,25  339)  =0 0=0

Получим .

(2  0+ 3+ 5  62)  59,75 = 0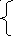

(7  0+ 3+  42)  40,25 = 0

 3+ 5  62 = 0

3+  42 = 0

4  20 = 0

4 = 20

= 5

3+ 5  5  62 = 0

3+ 25 62 = 0

3= 37

= .

Значение целевой функции на найденных ценах:

560  0 + 300  + 339  5 = 0 + 3700 +1695 = 5395 руб.

4. Решений двойственной задачи показало, что сырье первого вида использовано не полностью и его оценка у₁ = 0. Сырье 2-го и 3-го вида использованы полностью и имеют положительные оценки: у₂ =; у₃ = 5.

Таким образом, двойственные оценки определяют дефицитность используемого сырья. Величина двойственной оценки показывает, насколько вырастает максимальное значение целевой функции z прямой задачи при увеличении количества сырья соответствующего вида на 1 кг.

Увеличение сырья 2-го вида на 1 кг приведет к тому, что появится возможность найти новый оптимальный план, при котором общая прибыль от реализации увеличится на руб. При этом увеличение z может быть достигнуто при увеличении продукции В на единиц и сокращении продукции А на единицы. Вследствие этого остатки используемого сырья 3-го вида сократятся на кг.

Увеличение на 1 кг сырья 3-го вида позволяет найти такой план, при котором общая прибыль от выпуска изделий возрастает на 5 руб. Это будет достигнуто за счет увеличения изделия А на единицы и сокращения изделия В на 0,25, причем остатки используемого сырья 3-го вида увеличатся на кг.

При увеличении на 1 кг сырья 1-го вида значение функции z не изменится. Это означает, что сырье 1-го вида недефицитно.

5. При увеличении на 50 кг сырья, стоимость готовой продукции составит:

2х₁ + 7х₂  610

3х₁ + 3х₂  350

5х₁ + х₂  389

х₁  0, х₂  0

Т.к. у₂  0, у₃  0, то сырье 2-го и 3-го вида используются полностью, поэтому второе и третье условия выполняются как равенство:

3х₁ + 3х₂ = 350  3х₁ + 3х₂ = 350

5х₁ + х₂ = 389   3 15х₁ + 3х₂ = 1167

-12х₁ = -817

х₁ = .

х₂ = 389  5х1 = 389  5  =.

Получим новый оптимальный план: х₁ = единиц; х₂ = единиц.

При этом остатки сырья х4 = х5 = 0,

х3 = 610  2   7  ед.

6. Для определения целесообразности включения в план нового изделия с ценой 80 руб., если нормы затрат сырья 3, 5, 4 кг, рассчитаем стоимость ресурсов на изготовление единицы этого изделия в теневых ценах и сравним это значение с ценой реализации изделия:

 80 руб.

Следовательно, выпускать изделие С не выгодно, т.к. оно поглощает часть дефицитных ресурсов, и тем самым сдерживает рост выпуска выгодной продукции, что препятствует увеличению общей стоимости выпускаемых изделий. Если бы изделие С реализовалось по цене равной или большей руб., то его производство было бы выгодно.