Лабораторная работа №5

.3.doc

Скачиваний:

Добавлен:

08.05.2015

Размер:

134.14 Кб

Скачать

☆

Лабораторная работа №5.3

Циклические алгоритмические структуры

Цель работы

Научиться строить циклические алгоритмы, записывать алгоритмы в виде блок-схемы и на алгоритмическом языке.

Задание к лабораторной работе

По результатам работы необходимо в отчёте привести алгоритм в виде блок-схемы и на алгоритмическом языке (с необходимыми комментариями и пояснениями), а также привести контрольный пример, демонстрирующий правильность работы алгоритма. Форма отчёта приведена ниже.

Студенты, не имеющие с собой отчёта о предыдущей работе, к следующему занятию не допускаются с последующей отработкой пропущенного занятия!

Дан массив действительных чисел размером n . Получить новый массив, выбросив из исходной все члены с максимальным значением.
Записать алгоритм перевода действительного числа из десятичной системы счисления в восьмеричную систему счисления.
Задан массив действительных чисел 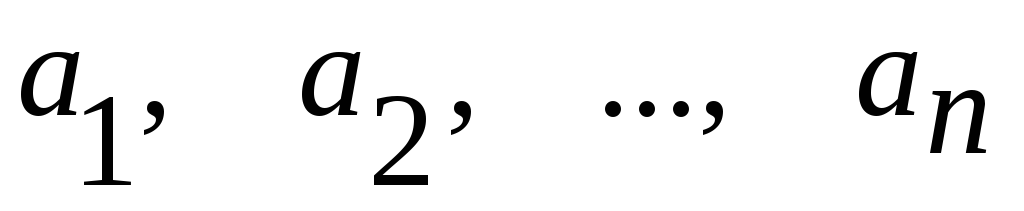. Все члены последовательности с четными номерами, предшествующие первому по порядку члену со значением 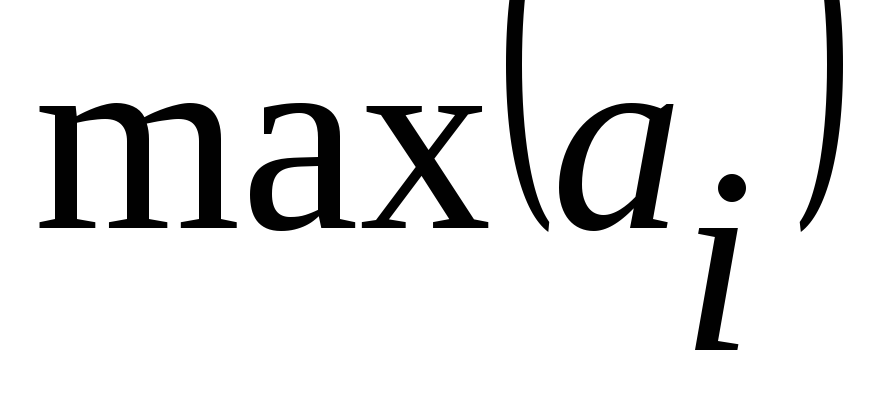домножить на .
Медиана. В массиве действительных чисел , не содержащем одинаковых элементов, найти средний по величине элемент, то есть такой, что в массиве ровно n элементов меньше его и столько же элементов больше его. При решении не допускается сортировать исходный массив и использовать дополнительные массивы.
Построить и записать алгоритм определения минимального элемента и его индекса в столбцах матрицы размером MN.
Задана квадратная матрица действительных чисел размера n. Переставить строку с максимальным элементом на главной диагонали со строкой с заданным номером. Найти среднее арифметическое элементов этих строк.
Из заданной квадратной матрицы действительных чисел размером n удалить строку и столбец на пересечении которых расположен минимальный элемент данной матрицы. Сформировать новую матрицу размером (n  1) и вывести ее по строкам.
Построить и записать алгоритм циклического сдвига одномерного массива на N шагов вправо или влево.
Записать алгоритм определения скалярного и векторного произведения двух векторов в координатной форме.
Записать алгоритм перевода действительного числа из десятичной системы счисления в двоичную систему счисления.
Даны два упорядоченных по возрастанию массива действительных чисел одинакового размера: и . Требуется за один просмотр объединить эти массивы в один массив размера 2n также упорядоченный по возрастанию.
Переместить элементы массива вправо на m позиций, при этом m элементов из конца массива перемещаются в начало. Например, результатом циклической перестановки исходного массива А = ( ) вправо на две позиции будет А = ( ).
Записать алгоритм перевода действительного числа из восьмеричной системы счисления в десятичную систему.
Касса. В одномерном массиве в порядке убывания представлены достоинства денежных знаков (купюр и монет) валютной системы некоторой страны. Реализовать выдачу в этой системе заданной суммы – m, минимальным числом денежных знаков.
Записать алгоритм, который проверяет, является ли введенная с клавиатуры квадратная матрица «магическим» квадратом. «Магическим» квадратом называется матрица, у которой сумма чисел в каждом горизонтальном или вертикальном ряду, а так же по каждой из диагоналей одна и та же.
Заданы два одномерных массива действительных чисел различных размеров. Объединить их в один массив, включив второй массив между k-м и (k+1)-м элементами первого.
Задан массив действительных чисел. Удалить из массива нулевые элементы, передвинув на их место следующие элементы без нарушения порядка их следования. В результате должен получиться массив меньшего размера, не содержащий нулей. Заводить новый массив не разрешается.
Отсев. Удалить в заданном массиве действительных чисел «лишние» (кроме первого) элементы так, чтобы оставшиеся образовывали возрастающую последовательность. Преобразование осуществить за один просмотр массива.
Дано натуральное число n. Сколько различных цифр встречается в его десятичной записи?
Колокол. В массиве действительных чисел наименьший элемент поместить на первое место, наименьший из оставшихся – на последнее место, следующий по величине – на второе место, следующий – на предпоследнее место и так далее – до середины массива.
Рассмотрим массив действительных чисел . Упорядочить данный массив по возрастанию, используя сортировку обменами. Алгоритм: Найти наименьшее i такое, что . Поменять и 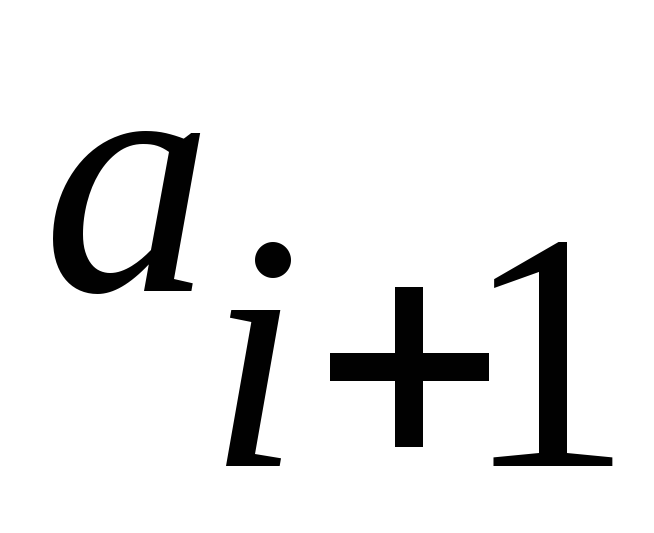местами , возобновить просмотр с элемента 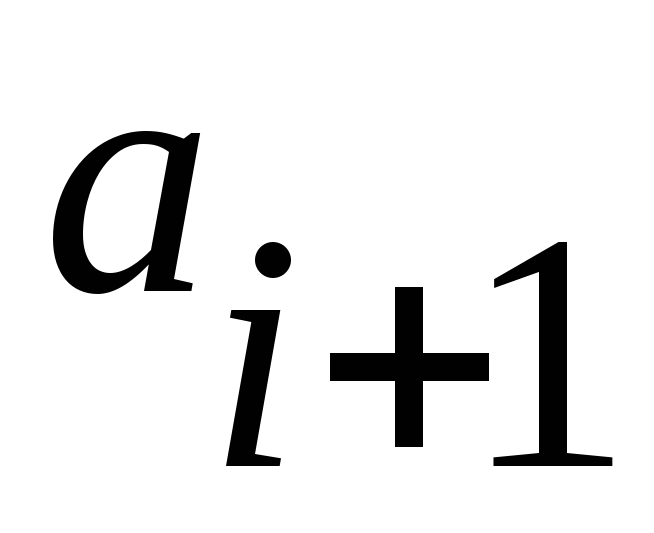и т.д. Тем самым наибольшее число передвинется на последнее место. Следующие просмотры начинать опять с начала, уменьшая на единицу количество просматриваемых элементов. Массив будет упорядочен после просмотра, в котором участвовали только его первый и второй элементы.
Задан массив действительных чисел . Переставить члены последовательности так, чтобы сначала расположились все ее неотрицательные члены, а потом – все отрицательные. Порядок следования, как среди неотрицательных членов, так и среди отрицательных должен быть сохранен прежним.
Рассмотрим массив действительных чисел . Упорядочить данный массив по возрастанию, используя сортировку линейным выбором. Алгоритм : найти элемент массива, имеющий наименьшее значение, переставить его с первым элементом, затем проделать то же самое , начав со второго элемента и т.д.
Элемент матрицы называется седловой точкой, если он является одновременно наименьшим в своей строке и наибольшим в столбце. Дана действительная матрица размером . Выяснить, имеются ли седловые точки в этой матрице, и если имеются, то указать индексы этих точек. Результат представить в виде таблицы.
Рассмотрим массив действительных чисел 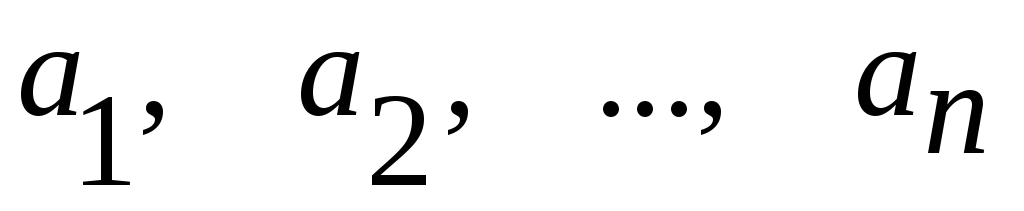. Упорядочить данный массив по возрастанию, используя сортировку простыми вставками. Алгоритм: просматривать последовательно и каждый новый элемент вставлять на подходящее место в уже упорядоченную последовательность . Это место определяется последовательным сравнением с упорядоченными элементами .
Рассмотрим массив действительных чисел . Упорядочить массив действительных чисел по возрастанию, используя алгоритм сортировки Шелла.
Дана действительная матрица размером , все элементы которой различны. В каждой строке выбрать элемент с наименьшим значением, затем среди этих чисел выбрать наибольшее. Указать индексы элемента с найденным значением.
Задана матрица размером . Найти максимальный по модулю элемент матрицы. Переставить строки и столбцы матрицы таким образом, чтобы максимальный по модулю элемент был расположен на пересечении 1-й строки и 1-го столбца.
Задана квадратная матрица действительных чисел A(n, n). Исключить из неё строку и столбец, на пересечении которых расположен максимальный элемент главной диагонали.
Дан массив действительных чисел размером n. Если в результате замены отрицательных членов последовательности их квадратами члены будут образовывать неубывающую последовательность, то получить сумму членов исходной последовательности. В противном случае получить их произведение.