2. Вычисление оценок математического ожидания и дисперсии

Оценки математического ожидания и дисперсии вычисляются по формулам

, ,(1)

где — частота вариантыв выборке объема.

Если объем выработки велик, то вычисление точечных оценок математического ожидания и дисперсии по формулам (1) громоздко. Для сокращения вычислений элементам выборки, попавшим в –тый интервал, припишем значения равные серединам интервалов

.

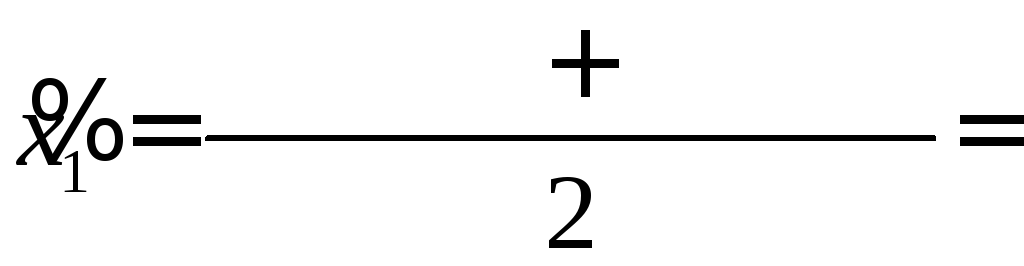
Вносим значения в пятый столбец таблицы 1.

Для упрощения дальнейших выкладок варианты заменяем наусловные варианты по формуле

,

где называетсяложным нулем (новым началом отсчета). Ложный ноль находим по следующему правилу:

Если число интервалов нечетное, то в качестве ложного нуля берем середину среднего интервала, если четное, то середину того интервала, у которого больше частота .

При этом варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.

Значения вносим в таблицу 1.

Подсчитаем произведения , результаты внесем в таблицу 1.

Суммируя седьмой столбец таблицы 1, вычислим значение

=

Оценим математическое ожидание по формуле

.

Подсчитаем произведения , результаты внесем в таблицу 1.

Суммируя восьмой столбец таблицы 1, вычислим значение

=

Оценим дисперсию по формуле

.

Оценка занижает дисперсию генеральной совокупности, поэтому введя поправочный коэффициент

получим несмещенную оценку дисперсии

.

Вычислим оценку среднего квадратического отклонения

.

Для сравнения подсчитаем по «правилу ». Так как для случайной величины, имеющей нормальное распределение, почти все рассеивания укладывается на участке , то с помощью «правила» можно ориентировочно определить оценку среднего квадратического отклонения случайной величины. Берем максимальное практически возможное отклонение от среднего значения и делим его на три.

Табл. 1

Статистическое распределение выборки
№ Кл.	Границы классов
1	2	3	4	5	6	7	8	9
	∑					h1= =	h2=

3. Построение гистограммы относительных частот

Гистограммой называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной , а высоты равны(плотность относительной частоты).

Для построения гистограммы заполним последний столбец таблицы 1. По полученным данным построим гистограмму:

По данным таблицы 1 построим точки с координатами и соединим их плавной пунктирной линией. Эта линия будет аналогом плотности распределения случайной величины и, следовательно, по виду гистограммы можно выдвинуть гипотезу о нормальном распределении (или о распределении, близком к нормальному) случайной величины с плотностью

В дальнейшем эту функцию будем называть теоретической плотностью распределения.