Вариант 18

1. Составьте математическую модель задачи.

Для нарезки заготовок длиной 20, 25 и 30 см используются прутки длиной 75 см. Требуется за смену нарезать следующее количество заготовок: длиной 20 см – 300 шт., 25 см – 270 шт., 30 см – 350 шт. Из одного прутка можно нарезать заготовки различной длины. Требуется определить, какое количество прутков необходимо разрезать каждым из возможных вариантов, чтобы число заготовок соответствовало заданной программе, и чтобы при этом общая длина всех концевых остатков была минимальной?

2. Решите графически задачу: найдите экстремумы функции , если,.

3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где – цена перевозки единицы груза из пунктав пункт.

6. Найдите решение матричной игры с матрицей .

Вариант 19

1. Составьте математическую модель задачи.

В обработку поступили две партии досок для изготовления комплектов из трех деталей, причем первая партия содержит 50 досок длиной по 6,5 м каждая, вторая содержит 200 досок длиной по 4 м каждая. Комплект состоит из двух деталей по 2 м каждая и одной детали длиной 1,5 м. Как распилить все доски, чтобы получить наибольшее число комплектов?

2. Решите графически задачу: найдите экстремумы функции , если,.

3. Дана задача линейного программирования

,

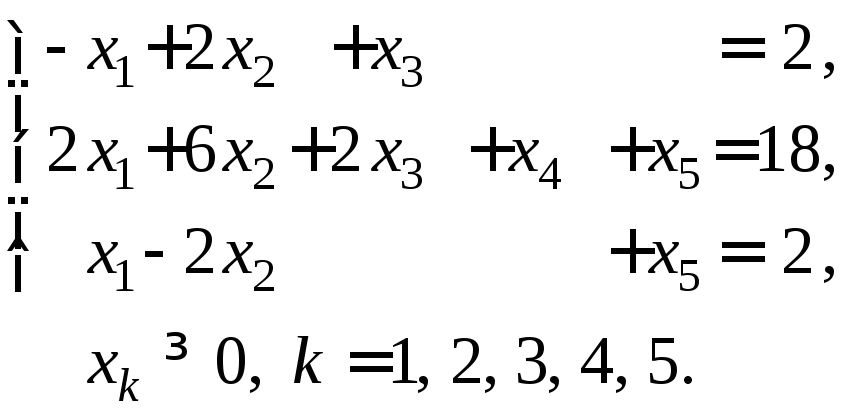
а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где – цена перевозки единицы груза из пунктав пункт.

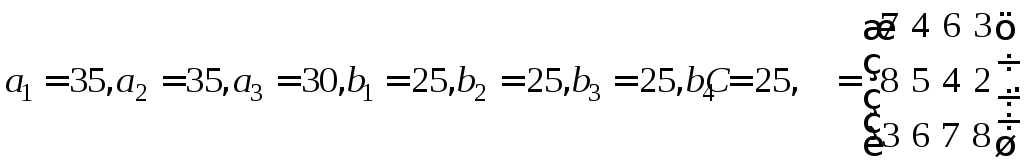
6. Найдите решение матричной игры с матрицей .

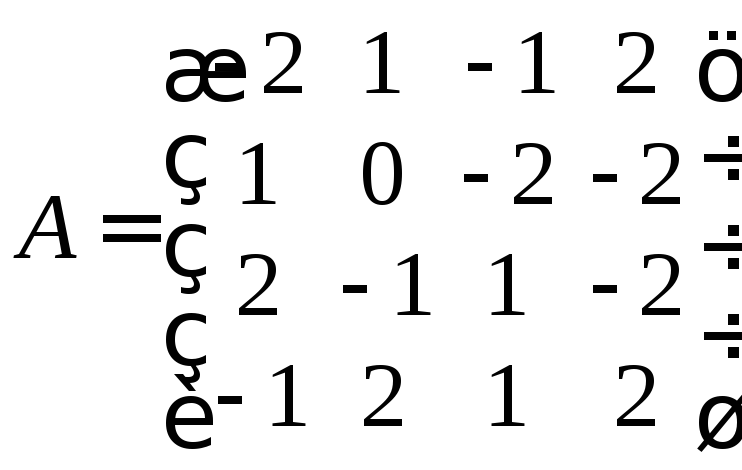Вариант 20

1. Составьте математическую модель задачи.

Фирма производит одежду для охотников, туристов и охранных структур. Дополнительно фирма решила изготавливать шапки и подстежки из натурального меха. Затраты на производство этих изделий и запасы сырья представлены в таблице. Спрос на шапки составляет не более 600 шт. в месяц, а подстежек – не более 400 шт. в месяц.

Сырье	Расход сырья на производство, дм		Средний запас в месяц, дм
	шапки	подстежки
Мех	22	140	61 600
Ткань	1,5	30	15 000
Оптовая цена, руб./шт.	410	840

Определить объемы производства этих изделий, обеспечивающих максимальный доход от продажи.

2. Решите графически задачу: найдите экстремумы функции , если,.

3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где – цена перевозки единицы груза из пунктав пункт.

6. Найдите решение матричной игры с матрицей .