Вариант 3

1. Составьте математическую модель задачи.

Из листового проката определенной формы необходимо вырезать некоторое количество заготовок двух типов (А и В) для производства 90 штук изделий. Для одного изделия требуется две заготовки типа А и 10 – типа В. Возможны четыре варианта раскроя одного листа проката. Количество заготовок А и В, вырезаемых из одного листа при каждом варианте раскроя, и отходы от раскроя даны в таблице.

№ варианта раскроя	Заготовки (шт.)		Отходы от раскроя (ед.)
	А	В
1	4	0	12
2	3	3	5
3	1	9	3
4	0	12	0

2. Решите графически задачу: найдите экстремумы функции , если,.

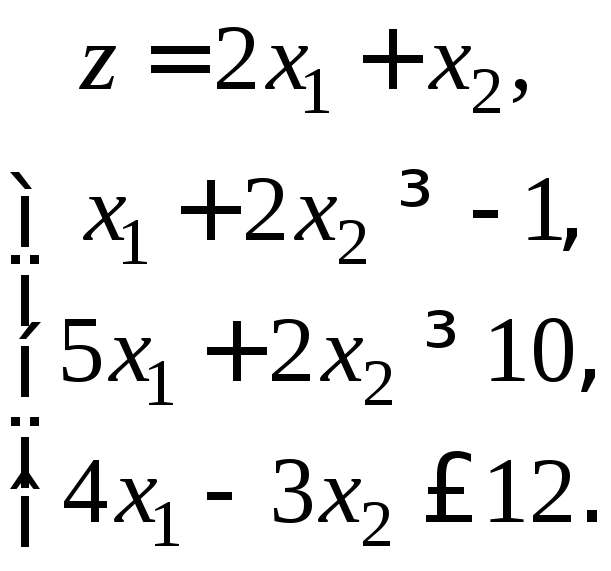
3. Дана задача линейного программирования

,

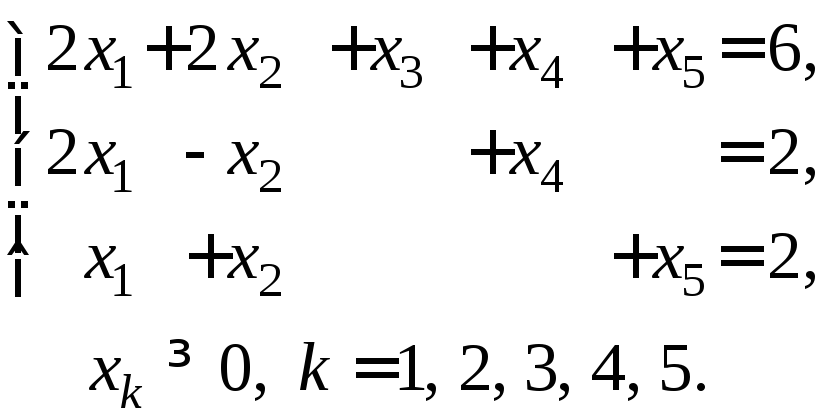
а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где – цена перевозки единицы груза из пунктав пункт.

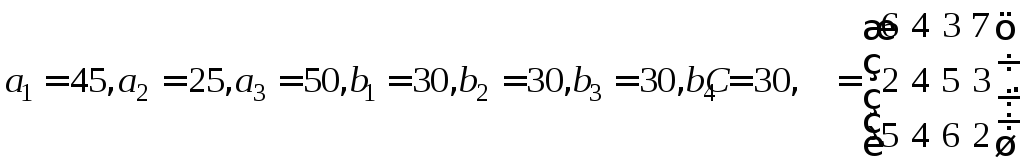
6. Найдите решение матричной игры с матрицей .

Вариант 4

1. Составьте математическую модель задачи.

Для производства двух видов продукции А и В предприятие использует четыре группы оборудования. В таблице указано время в часах, необходимое для производства одной единицы продукции для каждой группы оборудования. Также указано количество единиц каждого вида оборудования и стоимость одной единицы продукции при реализации.

Виды продукции	Группы оборудования				Стоимость ед. продукции (руб.)
	I	II	III	IV
A	1	2	5	2	4 000
B	1	1	3	2	6 000
Количество оборудования (шт.)	18	12	24	18

Составить план производства продукции предприятием, при котором оно получит наибольшую прибыль.

2. Решите графически задачу: найдите экстремумы функции , если,.

3. Дана задача линейного программирования

,

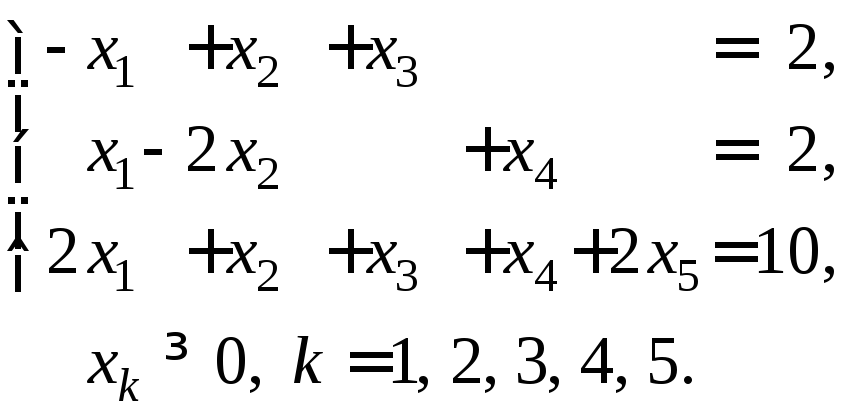
а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

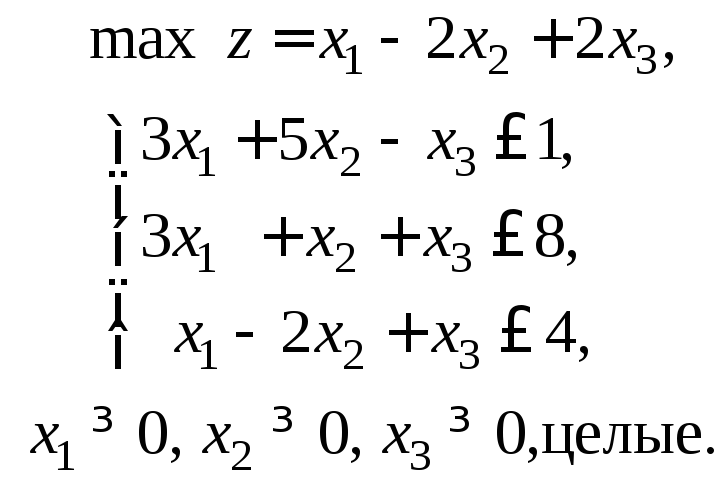
5. Решите методом потенциалов транспортную задачу, где – цена перевозки единицы груза из пунктав пункт.

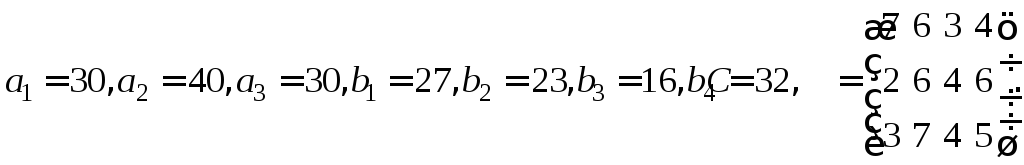
6. Найдите решение матричной игры с матрицей .

Вариант 5

1. Составьте математическую модель задачи.

В мастерской освоили производство столов и тумбочек. На их изготовление расходуется два вида древесины: I типа – 72 м³, и II типа – 56 м³. На каждое изделие требуется того и другого вида древесины в м³:

	I	II
Стол	0,18	0,08
Тумбочка	0,09	0,28

От производства одного стола получается чистого дохода 11 000 руб., а одной тумбочки – 7 000 руб. Сколько столов и тумбочек можно произвести из имеющегося материала, чтобы получить наибольшую прибыль?

2. Решите графически задачу: найдите экстремумы функции , если,.

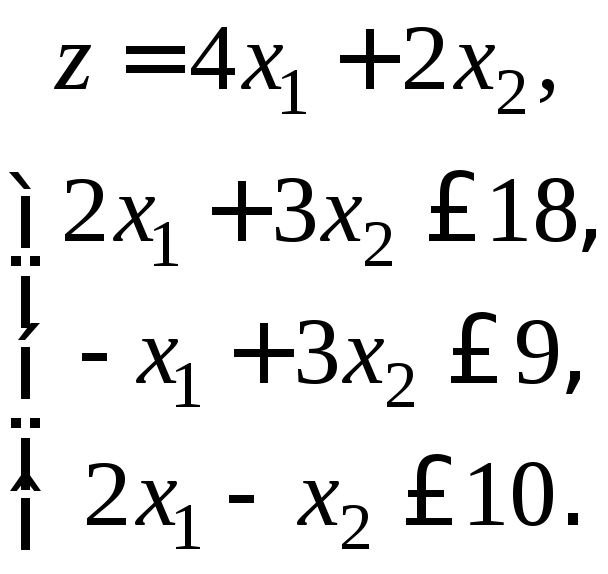
3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где – цена перевозки единицы груза из пунктав пункт.

6. Найдите решение матричной игры с матрицей .
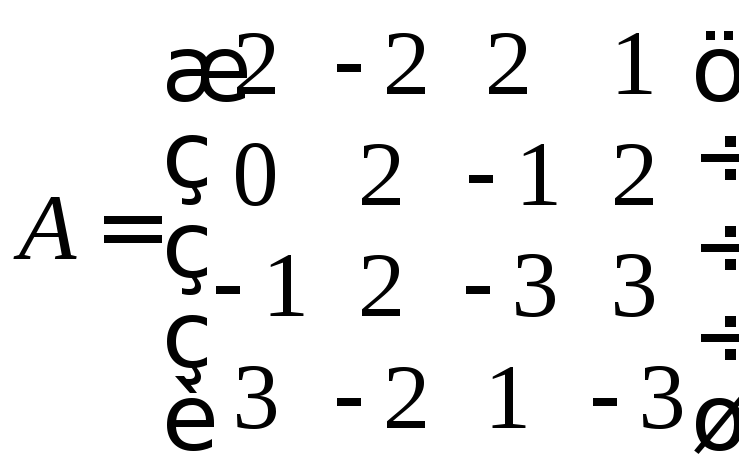